Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 139818 by Study last updated on 01/May/21

x^4 −22x^2 +x−114=0 x=?

$${x}^{\mathrm{4}} −\mathrm{22}{x}^{\mathrm{2}} +{x}−\mathrm{114}=\mathrm{0} \\ $$$${x}=? \\ $$

Answered by MJS_new last updated on 01/May/21

exact solution too complicated, approximation gives x_1 ≈−5.14749386 x_2 ≈5.11487664 x_(3, 4) ≈.0163086079±2.08076764i

$$\mathrm{exact}\:\mathrm{solution}\:\mathrm{too}\:\mathrm{complicated},\:\mathrm{approximation} \\ $$$$\mathrm{gives} \\ $$$${x}_{\mathrm{1}} \approx−\mathrm{5}.\mathrm{14749386} \\ $$$${x}_{\mathrm{2}} \approx\mathrm{5}.\mathrm{11487664} \\ $$$${x}_{\mathrm{3},\:\mathrm{4}} \approx.\mathrm{0163086079}\pm\mathrm{2}.\mathrm{08076764i} \\ $$

Commented by mr W last updated on 01/May/21

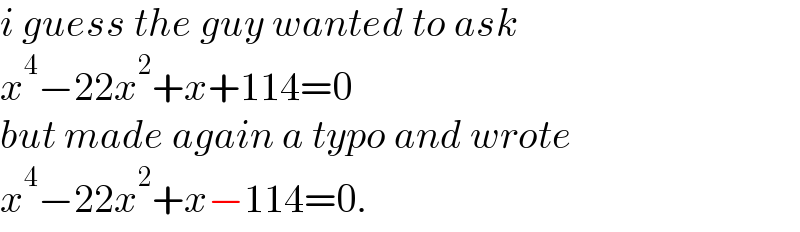
i guess the guy wanted to ask x^4 −22x^2 +x+114=0 but made again a typo and wrote x^4 −22x^2 +x−114=0.

$${i}\:{guess}\:{the}\:{guy}\:{wanted}\:{to}\:{ask} \\ $$$${x}^{\mathrm{4}} −\mathrm{22}{x}^{\mathrm{2}} +{x}+\mathrm{114}=\mathrm{0} \\ $$$${but}\:{made}\:{again}\:{a}\:{typo}\:{and}\:{wrote} \\ $$$${x}^{\mathrm{4}} −\mathrm{22}{x}^{\mathrm{2}} +{x}−\mathrm{114}=\mathrm{0}. \\ $$

Commented by MJS_new last updated on 01/May/21

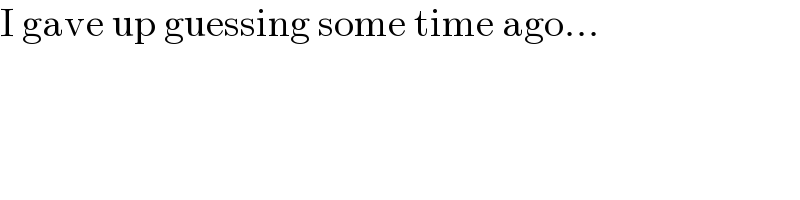
I gave up guessing some time ago...

$$\mathrm{I}\:\mathrm{gave}\:\mathrm{up}\:\mathrm{guessing}\:\mathrm{some}\:\mathrm{time}\:\mathrm{ago}... \\ $$

Answered by MJS_new last updated on 01/May/21

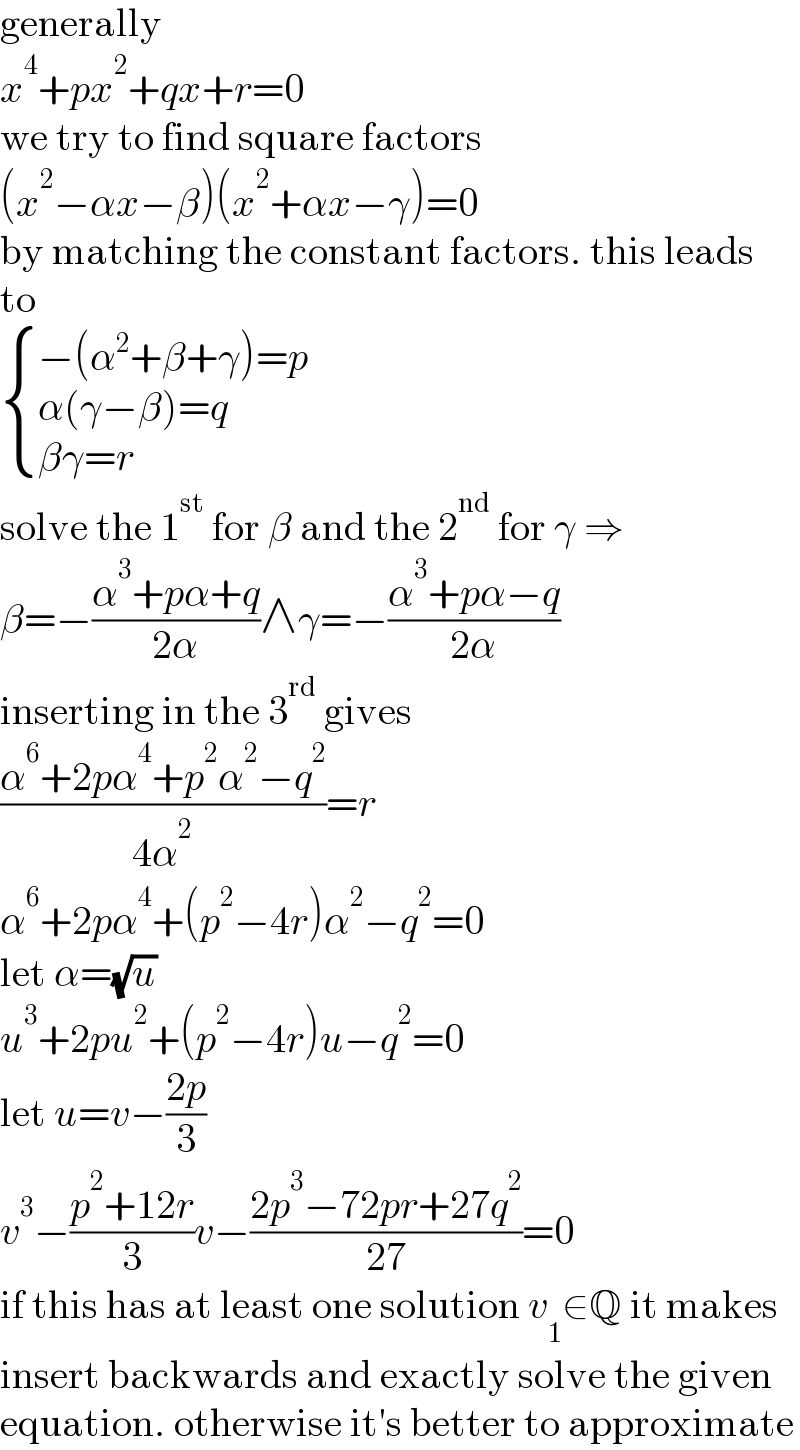
generally x^4 +px^2 +qx+r=0 we try to find square factors (x^2 −αx−β)(x^2 +αx−γ)=0 by matching the constant factors. this leads to { ((−(α^2 +β+γ)=p)),((α(γ−β)=q)),((βγ=r)) :} solve the 1^(st) for β and the 2^(nd) for γ ⇒ β=−((α^3 +pα+q)/(2α))∧γ=−((α^3 +pα−q)/(2α)) inserting in the 3^(rd) gives ((α^6 +2pα^4 +p^2 α^2 −q^2 )/(4α^2 ))=r α^6 +2pα^4 +(p^2 −4r)α^2 −q^2 =0 let α=(√u) u^3 +2pu^2 +(p^2 −4r)u−q^2 =0 let u=v−((2p)/3) v^3 −((p^2 +12r)/3)v−((2p^3 −72pr+27q^2 )/(27))=0 if this has at least one solution v_1 ∈Q it makes insert backwards and exactly solve the given equation. otherwise it′s better to approximate

$$\mathrm{generally} \\ $$$${x}^{\mathrm{4}} +{px}^{\mathrm{2}} +{qx}+{r}=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{try}\:\mathrm{to}\:\mathrm{find}\:\mathrm{square}\:\mathrm{factors} \\ $$$$\left({x}^{\mathrm{2}} −\alpha{x}−\beta\right)\left({x}^{\mathrm{2}} +\alpha{x}−\gamma\right)=\mathrm{0} \\ $$$$\mathrm{by}\:\mathrm{matching}\:\mathrm{the}\:\mathrm{constant}\:\mathrm{factors}.\:\mathrm{this}\:\mathrm{leads} \\ $$$$\mathrm{to} \\ $$$$\begin{cases}{−\left(\alpha^{\mathrm{2}} +\beta+\gamma\right)={p}}\\{\alpha\left(\gamma−\beta\right)={q}}\\{\beta\gamma={r}}\end{cases} \\ $$$$\mathrm{solve}\:\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{for}\:\beta\:\mathrm{and}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{for}\:\gamma\:\Rightarrow \\ $$$$\beta=−\frac{\alpha^{\mathrm{3}} +{p}\alpha+{q}}{\mathrm{2}\alpha}\wedge\gamma=−\frac{\alpha^{\mathrm{3}} +{p}\alpha−{q}}{\mathrm{2}\alpha} \\ $$$$\mathrm{inserting}\:\mathrm{in}\:\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{gives} \\ $$$$\frac{\alpha^{\mathrm{6}} +\mathrm{2}{p}\alpha^{\mathrm{4}} +{p}^{\mathrm{2}} \alpha^{\mathrm{2}} −{q}^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} }={r} \\ $$$$\alpha^{\mathrm{6}} +\mathrm{2}{p}\alpha^{\mathrm{4}} +\left({p}^{\mathrm{2}} −\mathrm{4}{r}\right)\alpha^{\mathrm{2}} −{q}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{let}\:\alpha=\sqrt{{u}} \\ $$$${u}^{\mathrm{3}} +\mathrm{2}{pu}^{\mathrm{2}} +\left({p}^{\mathrm{2}} −\mathrm{4}{r}\right){u}−{q}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{let}\:{u}={v}−\frac{\mathrm{2}{p}}{\mathrm{3}} \\ $$$${v}^{\mathrm{3}} −\frac{{p}^{\mathrm{2}} +\mathrm{12}{r}}{\mathrm{3}}{v}−\frac{\mathrm{2}{p}^{\mathrm{3}} −\mathrm{72}{pr}+\mathrm{27}{q}^{\mathrm{2}} }{\mathrm{27}}=\mathrm{0} \\ $$$$\mathrm{if}\:\mathrm{this}\:\mathrm{has}\:\mathrm{at}\:\mathrm{least}\:\mathrm{one}\:\mathrm{solution}\:{v}_{\mathrm{1}} \in\mathbb{Q}\:\mathrm{it}\:\mathrm{makes} \\ $$$$\mathrm{insert}\:\mathrm{backwards}\:\mathrm{and}\:\mathrm{exactly}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{given} \\ $$$$\mathrm{equation}.\:\mathrm{otherwise}\:\mathrm{it}'\mathrm{s}\:\mathrm{better}\:\mathrm{to}\:\mathrm{approximate} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com