
Question Number 201941 by ajfour last updated on 15/Dec/23
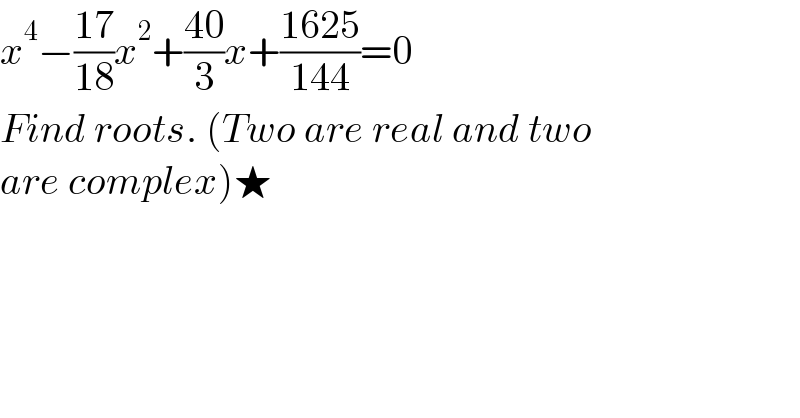
$${x}^{\mathrm{4}} −\frac{\mathrm{17}}{\mathrm{18}}{x}^{\mathrm{2}} +\frac{\mathrm{40}}{\mathrm{3}}{x}+\frac{\mathrm{1625}}{\mathrm{144}}=\mathrm{0} \\ $$$${Find}\:{roots}.\:\left({Two}\:{are}\:{real}\:{and}\:{two}\:\right. \\ $$$$\left.{are}\:{complex}\right)\bigstar \\ $$
Commented by Frix last updated on 17/Dec/23
![I use the common method. x^4 +px^2 +qx+r=0 matching with (x^2 −ux−v)(x^2 +ux−w)=0 leads to u=(√(s−((2p)/3))) where s is a solution of s^3 −(((p^2 +12r)s)/3)−((2p^3 −72pr+27q^2 )/(27))=0 v=−(p/2)−(q/(2u))+(u^2 /2) w=−(p/2)+(q/(2u))+(u^2 /2) [if there′s no useable s better approximate] In the given case p=−((17)/(18)) q=((40)/3) r=((1625)/(144)) ⇒ s=((226)/(27)) u=3 v=−((25)/4) w=−((65)/(36)) ⇒ x=−((13)/6)∨x=−(5/6)∨=(3/2)±2i How does your new method work?](Q201959.png)
$$\mathrm{I}\:\mathrm{use}\:\mathrm{the}\:\mathrm{common}\:\mathrm{method}. \\ $$$${x}^{\mathrm{4}} +{px}^{\mathrm{2}} +{qx}+{r}=\mathrm{0} \\ $$$$\mathrm{matching}\:\mathrm{with} \\ $$$$\left({x}^{\mathrm{2}} −{ux}−{v}\right)\left({x}^{\mathrm{2}} +{ux}−{w}\right)=\mathrm{0} \\ $$$$\mathrm{leads}\:\mathrm{to} \\ $$$${u}=\sqrt{{s}−\frac{\mathrm{2}{p}}{\mathrm{3}}} \\ $$$$\mathrm{where}\:{s}\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{of} \\ $$$${s}^{\mathrm{3}} −\frac{\left({p}^{\mathrm{2}} +\mathrm{12}{r}\right){s}}{\mathrm{3}}−\frac{\mathrm{2}{p}^{\mathrm{3}} −\mathrm{72}{pr}+\mathrm{27}{q}^{\mathrm{2}} }{\mathrm{27}}=\mathrm{0} \\ $$$${v}=−\frac{{p}}{\mathrm{2}}−\frac{{q}}{\mathrm{2}{u}}+\frac{{u}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${w}=−\frac{{p}}{\mathrm{2}}+\frac{{q}}{\mathrm{2}{u}}+\frac{{u}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\left[\mathrm{if}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{useable}\:{s}\:\mathrm{better}\:\mathrm{approximate}\right] \\ $$$$ \\ $$$$\mathrm{In}\:\mathrm{the}\:\mathrm{given}\:\mathrm{case} \\ $$$${p}=−\frac{\mathrm{17}}{\mathrm{18}}\:\:\:\:\:{q}=\frac{\mathrm{40}}{\mathrm{3}}\:\:\:\:\:{r}=\frac{\mathrm{1625}}{\mathrm{144}} \\ $$$$\Rightarrow \\ $$$${s}=\frac{\mathrm{226}}{\mathrm{27}} \\ $$$${u}=\mathrm{3}\:\:\:\:\:{v}=−\frac{\mathrm{25}}{\mathrm{4}}\:\:\:\:\:{w}=−\frac{\mathrm{65}}{\mathrm{36}} \\ $$$$\Rightarrow \\ $$$${x}=−\frac{\mathrm{13}}{\mathrm{6}}\vee{x}=−\frac{\mathrm{5}}{\mathrm{6}}\vee=\frac{\mathrm{3}}{\mathrm{2}}\pm\mathrm{2i} \\ $$$$ \\ $$$$\mathrm{How}\:\mathrm{does}\:\mathrm{your}\:\mathrm{new}\:\mathrm{method}\:\mathrm{work}? \\ $$
Answered by ajfour last updated on 17/Dec/23
![x^4 +bx^2 +cx+d=0 (2x^2 +px+h)(2x^2 −px+k)=3x^2 (x^2 +m) ⇒ p^2 {(p^2 +b)^2 −4d}=c^2 say p^2 =p_i ^2 (if three roots i=0,1,2) or p^2 =p_0 ^2 (if one root real) p^2 +m=−b x=((±p_0 )/2)±(√(−((c/(±2p_0 ))+(p^2 /4)+(b/2)))) All four roots obtained from any p=±p_i . This example p_0 =±3 (x∓(3/2))^2 =−[(1/(±6))(((40)/3))+(9/4)−((17)/(36))] (x∓(3/2))^2 =(4/9), −4 This method really never fails. because at least one p_i ^2 >0 always. As p^2 {(p^2 +b)^2 −4d}−c^2 =0 Its been 2 nights, i developed this.](Q201962.png)
$${x}^{\mathrm{4}} +{bx}^{\mathrm{2}} +{cx}+{d}=\mathrm{0} \\ $$$$\left(\mathrm{2}{x}^{\mathrm{2}} +{px}+{h}\right)\left(\mathrm{2}{x}^{\mathrm{2}} −{px}+{k}\right)=\mathrm{3}{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +{m}\right) \\ $$$$\Rightarrow\:\:{p}^{\mathrm{2}} \left\{\left({p}^{\mathrm{2}} +{b}\right)^{\mathrm{2}} −\mathrm{4}{d}\right\}={c}^{\mathrm{2}} \\ $$$$\:\:{say}\:\:\:{p}^{\mathrm{2}} ={p}_{{i}} ^{\mathrm{2}} \:\:\:\:\left({if}\:{three}\:{roots}\:\:{i}=\mathrm{0},\mathrm{1},\mathrm{2}\right) \\ $$$$\:\:\:\:\:{or}\:\:\:{p}^{\mathrm{2}} ={p}_{\mathrm{0}} ^{\mathrm{2}} \:\:\:\left({if}\:{one}\:{root}\:{real}\right) \\ $$$${p}^{\mathrm{2}} +{m}=−{b} \\ $$$${x}=\frac{\pm{p}_{\mathrm{0}} }{\mathrm{2}}\pm\sqrt{−\left(\frac{{c}}{\pm\mathrm{2}{p}_{\mathrm{0}} }+\frac{{p}^{\mathrm{2}} }{\mathrm{4}}+\frac{{b}}{\mathrm{2}}\right)} \\ $$$${All}\:{four}\:{roots}\:{obtained}\:{from}\:{any} \\ $$$${p}=\pm{p}_{{i}} \:\:. \\ $$$${This}\:{example}\:\:\:\:{p}_{\mathrm{0}} =\pm\mathrm{3} \\ $$$$\left({x}\mp\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} =−\left[\frac{\mathrm{1}}{\pm\mathrm{6}}\left(\frac{\mathrm{40}}{\mathrm{3}}\right)+\frac{\mathrm{9}}{\mathrm{4}}−\frac{\mathrm{17}}{\mathrm{36}}\right]\: \\ $$$$\left({x}\mp\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{9}},\:−\mathrm{4} \\ $$$${This}\:{method}\:{really}\:{never}\:{fails}. \\ $$$${because}\:{at}\:{least}\:{one}\:{p}_{{i}} ^{\mathrm{2}} >\mathrm{0}\:{always}.\:{As} \\ $$$${p}^{\mathrm{2}} \left\{\left({p}^{\mathrm{2}} +{b}\right)^{\mathrm{2}} −\mathrm{4}{d}\right\}−{c}^{\mathrm{2}} =\mathrm{0} \\ $$$${Its}\:{been}\:\mathrm{2}\:{nights},\:{i}\:{developed}\:{this}. \\ $$
Commented by Frix last updated on 17/Dec/23
From my version: s^3 −(p^2 +12r)s/3−(2p^3 −72pr+27q^2)/27=0 u=√(s−2p/3) u^6 +2pu^4 +(p^2 −4r)u^2 −q^2 =0 From your version: p^2 ((p^2 +b)^2 −4d)−c^2 =0 p^6 +2bp^4 +(b^2 −4d)p^2 −c^2 =0 ...so it′s basically the same... ������
Answered by ajfour last updated on 17/Dec/23

Commented by ajfour last updated on 17/Dec/23
Shouldn't i be awarded for this?
