
Question Number 126994 by bramlexs22 last updated on 26/Dec/20
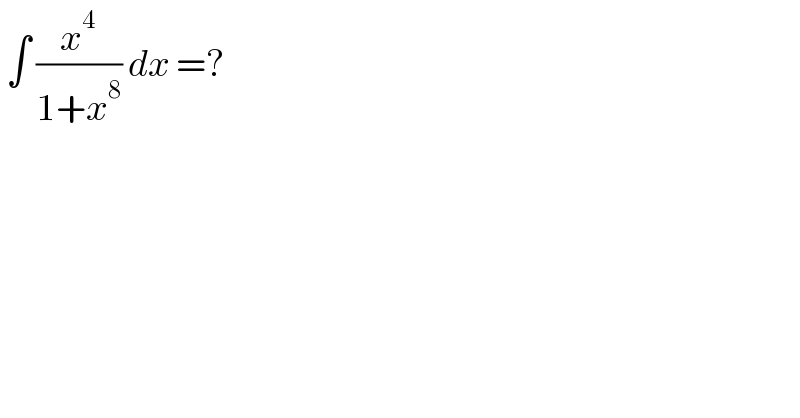
$$\:\int\:\frac{{x}^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{8}} }\:{dx}\:=? \\ $$
Answered by liberty last updated on 26/Dec/20
![Ω=∫(x^4 /(1+x^8 )) dx = ∫(dx/(x^4 +(1/x^4 ))) =∫(dx/((x^2 +(1/x^2 ))^2 −2)) Ω=∫(dx/((x^2 +(1/x^2 )+(√2))(x^2 +(1/x^2 )−(√2)))) Ω=((√2)/4)∫((dx/((x^2 +(1/x^2 )−(√2))))−(dx/((x^2 +(1/x^2 )+(√2))))) Ω=((√2)/8) [∫(((1−(1/x^2 ))+(1+(1/x^2 )))/(x^2 +(1/x^2 )−(√2)))dx −∫ (((1−(1/x^2 ))+(1+(1/x^2 )))/(x^2 +(1/x^2 )+(√2)))dx ] Ω=((√2)/8) [∫((d(x+(1/x)))/((x+(1/x))^2 −(2+(√2))))+∫((d(x−(1/x)))/((x−(1/x))^2 +(2−(√2))))] −((√2)/8) [∫((d(x+(1/x)))/((x+(1/x))^2 −(2−(√2))))+∫((d(x−(1/x)))/((x−(1/x))^2 +(2+(√2))))] Ω=((√2)/8) [ (1/(2(√(2+(√2))))) ln ∣((x^2 −x(√(2+(√2))) +1)/(x^2 +x(√(2+(√2))) +1)) ∣ + (1/( (√(2−(√2))))) tan^(−1) (((x^2 −1)/(x(√(2−(√2))))))−(1/(2(√(2−(√2)))))ln ∣((x^2 −x(√(2−(√2)))+1)/(x^2 +x(√(2−(√2)))+1))∣ −(1/( (√(2−(√2))))) tan^(−1) (((x^2 +1)/(x(√(2+(√2)))))) ] + c](Q126995.png)
$$\Omega=\int\frac{{x}^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{8}} }\:{dx}\:=\:\int\frac{{dx}}{{x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }}\:=\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$$\Omega=\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\sqrt{\mathrm{2}}\right)\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\sqrt{\mathrm{2}}\right)}\: \\ $$$$\Omega=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\int\left(\frac{{dx}}{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\sqrt{\mathrm{2}}\right)}−\frac{{dx}}{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\sqrt{\mathrm{2}}\right)}\right) \\ $$$$\Omega=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\:\left[\int\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)+\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\sqrt{\mathrm{2}}}{dx}\:−\int\:\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)+\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\sqrt{\mathrm{2}}}{dx}\:\right] \\ $$$$\Omega=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\:\left[\int\frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)}+\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)}\right] \\ $$$$\:\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\:\left[\int\frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)}+\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)}\right] \\ $$$$\Omega=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\:\left[\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}\:\mathrm{ln}\:\mid\frac{{x}^{\mathrm{2}} −{x}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}\:+\mathrm{1}}{{x}^{\mathrm{2}} +{x}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}\:+\mathrm{1}}\:\mid\:+\right. \\ $$$$\:\:\:\:\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}\mathrm{ln}\:\mid\frac{{x}^{\mathrm{2}} −{x}\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}+\mathrm{1}}\mid \\ $$$$\left.\:\:\:\:\:\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}\right)\:\right]\:+\:{c}\: \\ $$
Commented by bramlexs22 last updated on 26/Dec/20

$${waw}.... \\ $$
