
Question Number 188351 by TUN last updated on 28/Feb/23
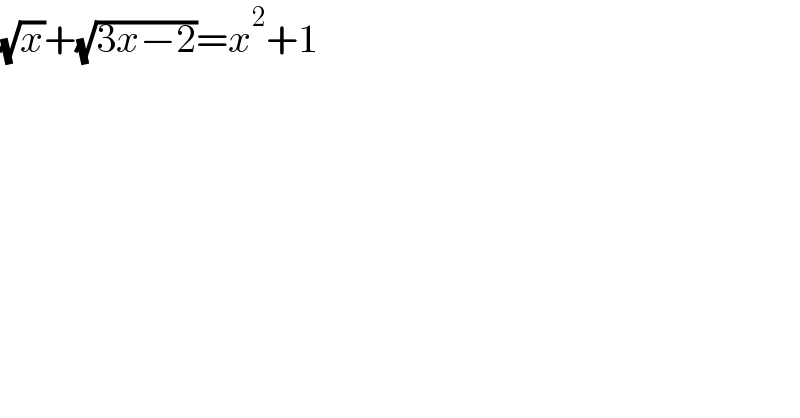
$$\sqrt{{x}}+\sqrt{\mathrm{3}{x}−\mathrm{2}}={x}^{\mathrm{2}} +\mathrm{1} \\ $$
Answered by MJS_new last updated on 28/Feb/23
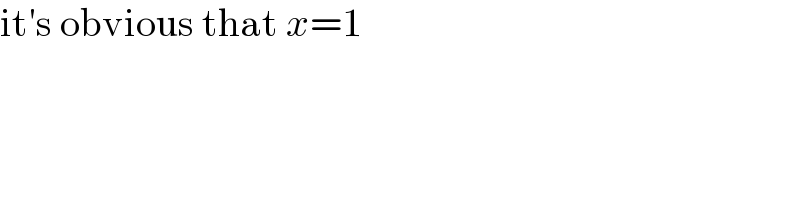
$$\mathrm{it}'\mathrm{s}\:\mathrm{obvious}\:\mathrm{that}\:{x}=\mathrm{1} \\ $$
Commented by TUN last updated on 28/Feb/23

$${step}\:{by}\:{step}\:¿ \\ $$
Commented by Humble last updated on 28/Feb/23

$${too}\:{bulky} \\ $$
Commented by MJS_new last updated on 28/Feb/23
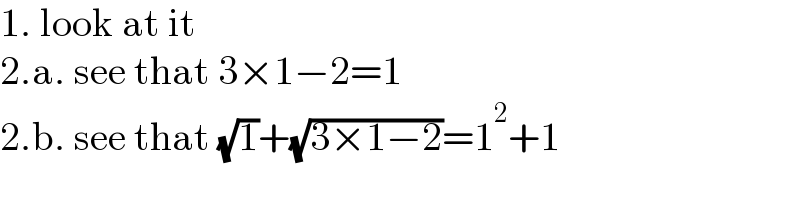
$$\mathrm{1}.\:\mathrm{look}\:\mathrm{at}\:\mathrm{it} \\ $$$$\mathrm{2}.\mathrm{a}.\:\mathrm{see}\:\mathrm{that}\:\mathrm{3}×\mathrm{1}−\mathrm{2}=\mathrm{1} \\ $$$$\mathrm{2}.\mathrm{b}.\:\mathrm{see}\:\mathrm{that}\:\sqrt{\mathrm{1}}+\sqrt{\mathrm{3}×\mathrm{1}−\mathrm{2}}=\mathrm{1}^{\mathrm{2}} +\mathrm{1} \\ $$
Answered by manxsol last updated on 01/Mar/23

$$\begin{array}{|c|c|c|c|c|}{{f}\left({x}\right)}&\hline{{g}\left({x}\right)}&\hline{\cap\:{x}=}\\{\sqrt{{x}}}&\hline{{x}^{\mathrm{2}} }&\hline{\mathrm{1}}\\{\sqrt{\mathrm{3}{x}−\mathrm{2}}}&\hline{{x}^{\mathrm{2}} }&\hline{\mathrm{1}}\\{\sqrt{{x}}+\sqrt{\mathrm{3}{x}−\mathrm{2}}}&\hline{\mathrm{2}{x}^{\mathrm{2}} }&\hline{=\mathrm{2}}\\{\sqrt{{x}}+\sqrt{\mathrm{3}{x}−\mathrm{2}}}&\hline{{x}^{\mathrm{2}} +\mathrm{1}}&\hline{=\mathrm{2}}\\\hline\end{array} \\ $$$${solucion}\:{x}=\mathrm{1} \\ $$$$ \\ $$
