
Question Number 136304 by aurpeyz last updated on 20/Mar/21
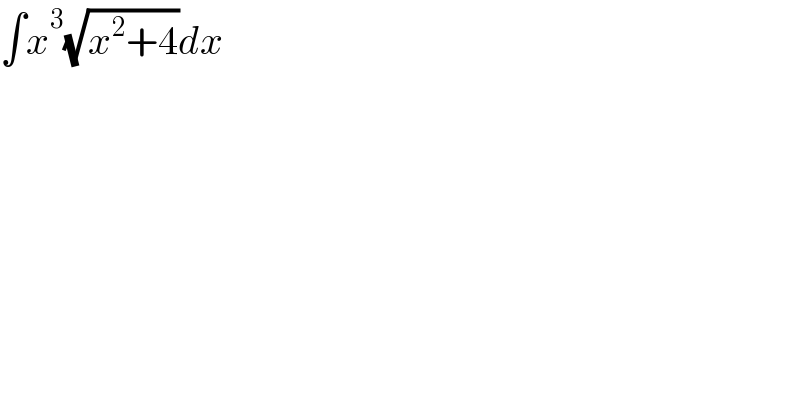
$$\int{x}^{\mathrm{3}} \sqrt{{x}^{\mathrm{2}} +\mathrm{4}}{dx} \\ $$
Answered by liberty last updated on 20/Mar/21
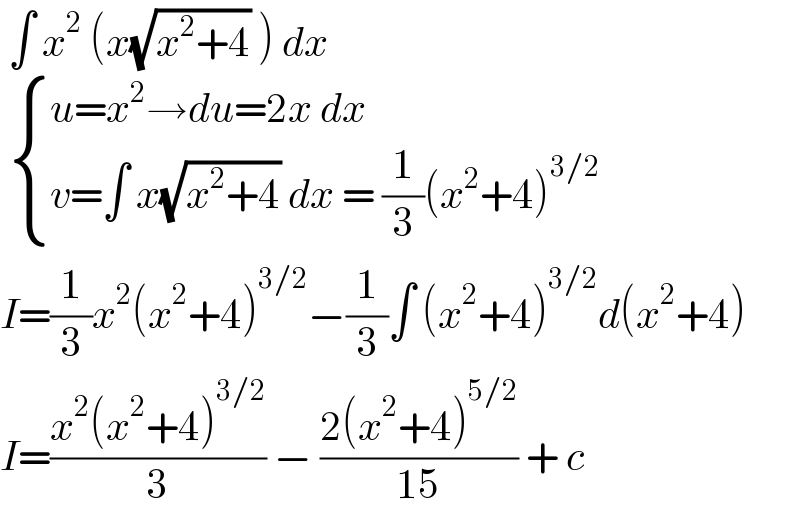
$$\:\int\:{x}^{\mathrm{2}} \:\left({x}\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}\:\right)\:{dx}\: \\ $$$$\:\begin{cases}{{u}={x}^{\mathrm{2}} \rightarrow{du}=\mathrm{2}{x}\:{dx}}\\{{v}=\int\:{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}\:{dx}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{3}/\mathrm{2}} }\end{cases} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{3}/\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\int\:\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{3}/\mathrm{2}} {d}\left({x}^{\mathrm{2}} +\mathrm{4}\right) \\ $$$${I}=\frac{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{3}/\mathrm{2}} }{\mathrm{3}}\:−\:\frac{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{5}/\mathrm{2}} }{\mathrm{15}}\:+\:{c} \\ $$
