
Question Number 142653 by Gbenga last updated on 03/Jun/21

$${x}^{\mathrm{3}} .{e}^{{x}} =\mathrm{216} \\ $$
Answered by MJS_new last updated on 03/Jun/21
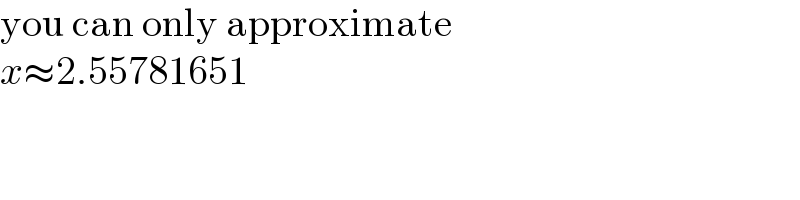
$$\mathrm{you}\:\mathrm{can}\:\mathrm{only}\:\mathrm{approximate} \\ $$$${x}\approx\mathrm{2}.\mathrm{55781651} \\ $$
Commented by mr W last updated on 03/Jun/21
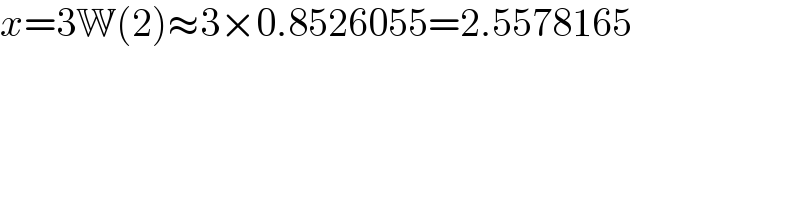
$${x}=\mathrm{3}\mathbb{W}\left(\mathrm{2}\right)\approx\mathrm{3}×\mathrm{0}.\mathrm{8526055}=\mathrm{2}.\mathrm{5578165} \\ $$
Answered by mr W last updated on 04/Jun/21
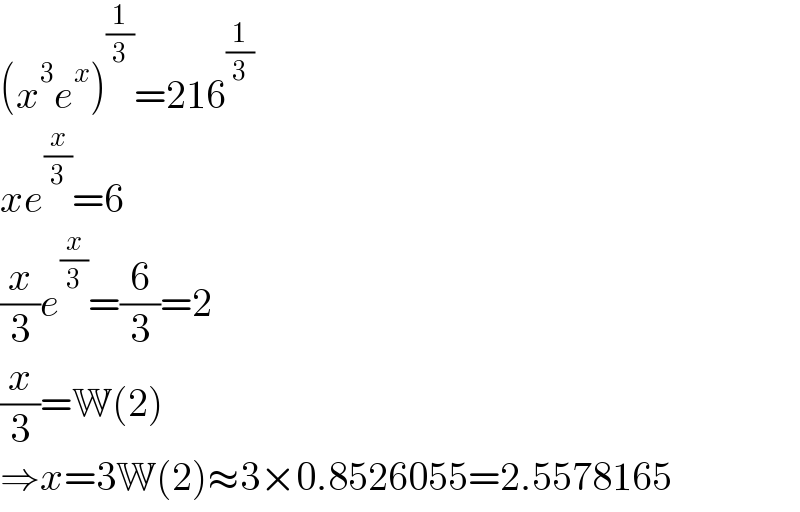
$$\left({x}^{\mathrm{3}} {e}^{{x}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} =\mathrm{216}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${xe}^{\frac{{x}}{\mathrm{3}}} =\mathrm{6} \\ $$$$\frac{{x}}{\mathrm{3}}{e}^{\frac{{x}}{\mathrm{3}}} =\frac{\mathrm{6}}{\mathrm{3}}=\mathrm{2} \\ $$$$\frac{{x}}{\mathrm{3}}=\mathbb{W}\left(\mathrm{2}\right) \\ $$$$\Rightarrow{x}=\mathrm{3}\mathbb{W}\left(\mathrm{2}\right)\approx\mathrm{3}×\mathrm{0}.\mathrm{8526055}=\mathrm{2}.\mathrm{5578165} \\ $$
