Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 153245 by liberty last updated on 06/Sep/21

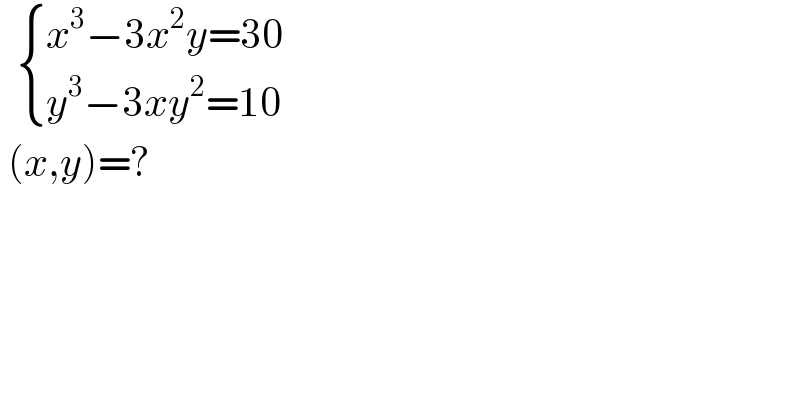
{ ((x^3 −3x^2 y=30)),((y^3 −3xy^2 =10)) :} (x,y)=?

$$\:\:\begin{cases}{{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} {y}=\mathrm{30}}\\{{y}^{\mathrm{3}} −\mathrm{3}{xy}^{\mathrm{2}} =\mathrm{10}}\end{cases} \\ $$$$\:\left({x},{y}\right)=? \\ $$

Answered by Rasheed.Sindhi last updated on 06/Sep/21

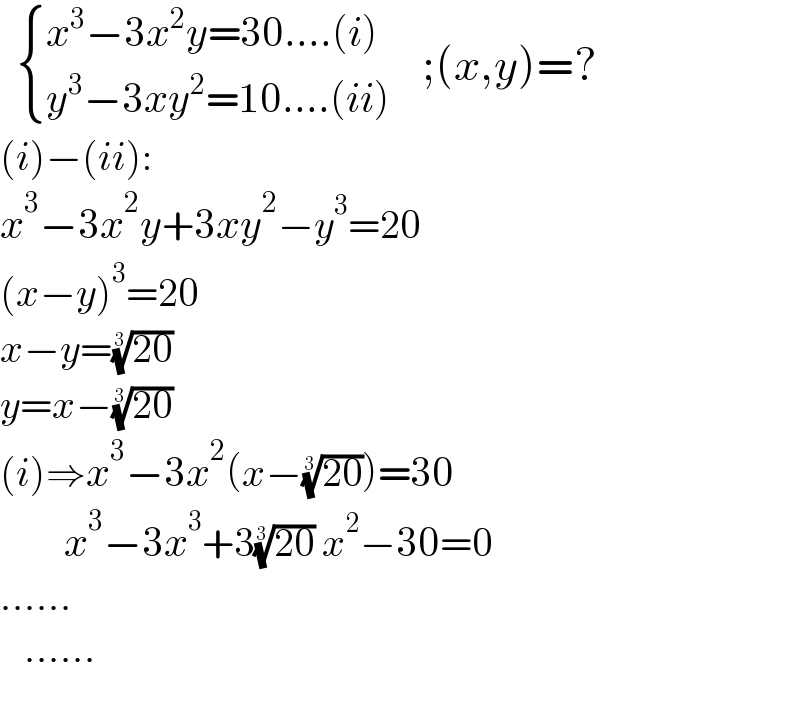
{ ((x^3 −3x^2 y=30....(i))),((y^3 −3xy^2 =10....(ii))) :} ;(x,y)=? (i)−(ii): x^3 −3x^2 y+3xy^2 −y^3 =20 (x−y)^3 =20 x−y=((20))^(1/3) y=x−((20))^(1/3) (i)⇒x^3 −3x^2 (x−((20))^(1/3) )=30 x^3 −3x^3 +3((20))^(1/3) x^2 −30=0 ...... ......

$$\:\:\begin{cases}{{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} {y}=\mathrm{30}....\left({i}\right)}\\{{y}^{\mathrm{3}} −\mathrm{3}{xy}^{\mathrm{2}} =\mathrm{10}....\left({ii}\right)}\end{cases}\:\:\:\:;\left({x},{y}\right)=? \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} {y}+\mathrm{3}{xy}^{\mathrm{2}} −{y}^{\mathrm{3}} =\mathrm{20} \\ $$$$\left({x}−{y}\right)^{\mathrm{3}} =\mathrm{20} \\ $$$${x}−{y}=\sqrt[{\mathrm{3}}]{\mathrm{20}} \\ $$$${y}={x}−\sqrt[{\mathrm{3}}]{\mathrm{20}} \\ $$$$\left({i}\right)\Rightarrow{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} \left({x}−\sqrt[{\mathrm{3}}]{\mathrm{20}}\right)=\mathrm{30} \\ $$$$\:\:\:\:\:\:\:\:{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{3}} +\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{20}}\:{x}^{\mathrm{2}} −\mathrm{30}=\mathrm{0} \\ $$$$...... \\ $$$$\:\:\:...... \\ $$$$ \\ $$

Commented by amin96 last updated on 06/Sep/21

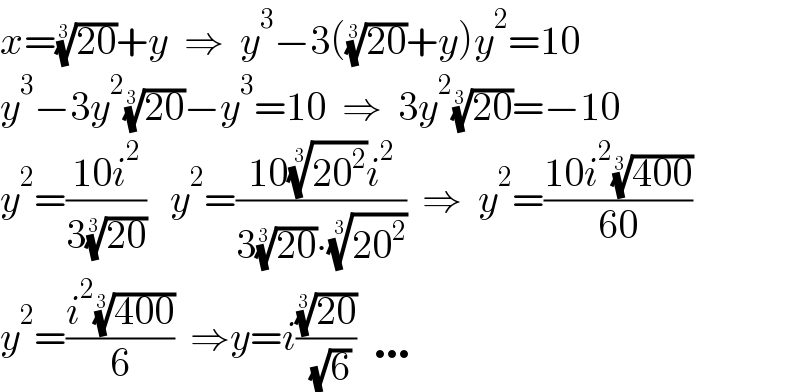
x=((20))^(1/3) +y ⇒ y^3 −3(((20))^(1/3) +y)y^2 =10 y^3 −3y^2 ((20))^(1/3) −y^3 =10 ⇒ 3y^2 ((20))^(1/3) =−10 y^2 =((10i^2 )/(3((20))^(1/3) )) y^2 =((10((20^2 ))^(1/3) i^2 )/(3((20))^(1/3) ∙((20^2 ))^(1/3) )) ⇒ y^2 =((10i^2 ((400))^(1/3) )/(60)) y^2 =((i^2 ((400))^(1/3) )/6) ⇒y=i(((20))^(1/3) /( (√6))) …

$${x}=\sqrt[{\mathrm{3}}]{\mathrm{20}}+{y}\:\:\Rightarrow\:\:{y}^{\mathrm{3}} −\mathrm{3}\left(\sqrt[{\mathrm{3}}]{\mathrm{20}}+{y}\right){y}^{\mathrm{2}} =\mathrm{10} \\ $$$${y}^{\mathrm{3}} −\mathrm{3}{y}^{\mathrm{2}} \sqrt[{\mathrm{3}}]{\mathrm{20}}−{y}^{\mathrm{3}} =\mathrm{10}\:\:\Rightarrow\:\:\mathrm{3}{y}^{\mathrm{2}} \sqrt[{\mathrm{3}}]{\mathrm{20}}=−\mathrm{10}\:\: \\ $$$${y}^{\mathrm{2}} =\frac{\mathrm{10}{i}^{\mathrm{2}} }{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{20}}}\:\:\:{y}^{\mathrm{2}} =\frac{\mathrm{10}\sqrt[{\mathrm{3}}]{\mathrm{20}^{\mathrm{2}} }{i}^{\mathrm{2}} }{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{20}}\centerdot\sqrt[{\mathrm{3}}]{\mathrm{20}^{\mathrm{2}} }}\:\:\Rightarrow\:\:{y}^{\mathrm{2}} =\frac{\mathrm{10}{i}^{\mathrm{2}} \sqrt[{\mathrm{3}}]{\mathrm{400}}}{\mathrm{60}} \\ $$$${y}^{\mathrm{2}} =\frac{{i}^{\mathrm{2}} \sqrt[{\mathrm{3}}]{\mathrm{400}}}{\mathrm{6}}\:\:\Rightarrow{y}={i}\frac{\sqrt[{\mathrm{3}}]{\mathrm{20}}}{\:\sqrt{\mathrm{6}}}\:\:\ldots \\ $$

Commented by liberty last updated on 06/Sep/21

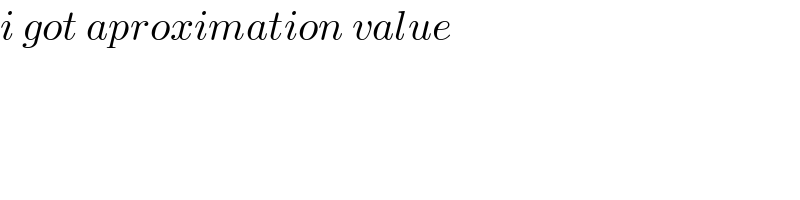
i got aproximation value

$${i}\:{got}\:{aproximation}\:{value} \\ $$

Answered by mr W last updated on 06/Sep/21

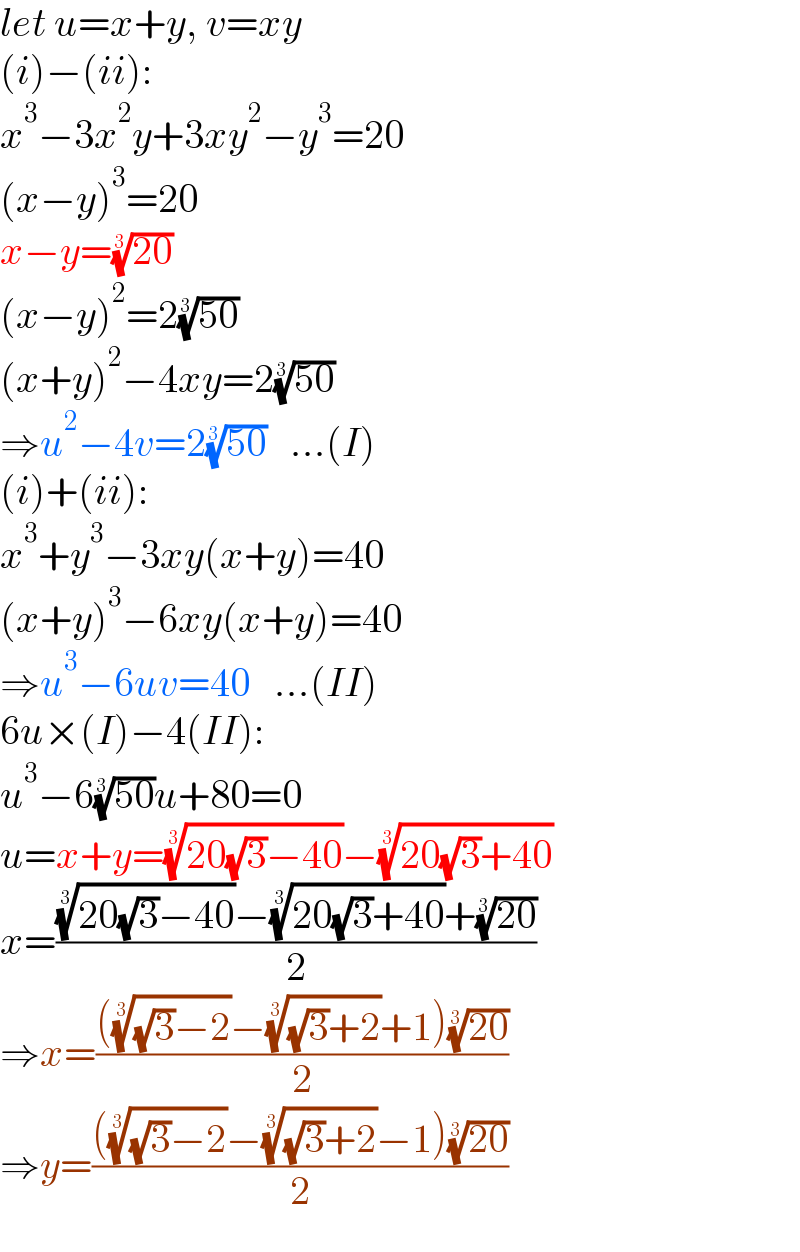
let u=x+y, v=xy (i)−(ii): x^3 −3x^2 y+3xy^2 −y^3 =20 (x−y)^3 =20 x−y=((20))^(1/3) (x−y)^2 =2((50))^(1/3) (x+y)^2 −4xy=2((50))^(1/3) ⇒u^2 −4v=2((50))^(1/3) ...(I) (i)+(ii): x^3 +y^3 −3xy(x+y)=40 (x+y)^3 −6xy(x+y)=40 ⇒u^3 −6uv=40 ...(II) 6u×(I)−4(II): u^3 −6((50))^(1/3) u+80=0 u=x+y=((20(√3)−40))^(1/3) −((20(√3)+40))^(1/3) x=((((20(√3)−40))^(1/3) −((20(√3)+40))^(1/3) +((20))^(1/3) )/2) ⇒x=((((((√3)−2))^(1/3) −(((√3)+2))^(1/3) +1)((20))^(1/3) )/2) ⇒y=((((((√3)−2))^(1/3) −(((√3)+2))^(1/3) −1)((20))^(1/3) )/2)

$${let}\:{u}={x}+{y},\:{v}={xy} \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} {y}+\mathrm{3}{xy}^{\mathrm{2}} −{y}^{\mathrm{3}} =\mathrm{20} \\ $$$$\left({x}−{y}\right)^{\mathrm{3}} =\mathrm{20} \\ $$$${x}−{y}=\sqrt[{\mathrm{3}}]{\mathrm{20}} \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} =\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{50}} \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{4}{xy}=\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{50}} \\ $$$$\Rightarrow{u}^{\mathrm{2}} −\mathrm{4}{v}=\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{50}}\:\:\:...\left({I}\right) \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} −\mathrm{3}{xy}\left({x}+{y}\right)=\mathrm{40} \\ $$$$\left({x}+{y}\right)^{\mathrm{3}} −\mathrm{6}{xy}\left({x}+{y}\right)=\mathrm{40} \\ $$$$\Rightarrow{u}^{\mathrm{3}} −\mathrm{6}{uv}=\mathrm{40}\:\:\:...\left({II}\right) \\ $$$$\mathrm{6}{u}×\left({I}\right)−\mathrm{4}\left({II}\right): \\ $$$${u}^{\mathrm{3}} −\mathrm{6}\sqrt[{\mathrm{3}}]{\mathrm{50}}{u}+\mathrm{80}=\mathrm{0} \\ $$$${u}={x}+{y}=\sqrt[{\mathrm{3}}]{\mathrm{20}\sqrt{\mathrm{3}}−\mathrm{40}}−\sqrt[{\mathrm{3}}]{\mathrm{20}\sqrt{\mathrm{3}}+\mathrm{40}} \\ $$$${x}=\frac{\sqrt[{\mathrm{3}}]{\mathrm{20}\sqrt{\mathrm{3}}−\mathrm{40}}−\sqrt[{\mathrm{3}}]{\mathrm{20}\sqrt{\mathrm{3}}+\mathrm{40}}+\sqrt[{\mathrm{3}}]{\mathrm{20}}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\left(\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{3}}−\mathrm{2}}−\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{3}}+\mathrm{2}}+\mathrm{1}\right)\sqrt[{\mathrm{3}}]{\mathrm{20}}}{\mathrm{2}} \\ $$$$\Rightarrow{y}=\frac{\left(\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{3}}−\mathrm{2}}−\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{3}}+\mathrm{2}}−\mathrm{1}\right)\sqrt[{\mathrm{3}}]{\mathrm{20}}}{\mathrm{2}} \\ $$

Commented by liberty last updated on 06/Sep/21

thank you

$${thank}\:{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com