
Question Number 217985 by hardmath last updated on 24/Mar/25
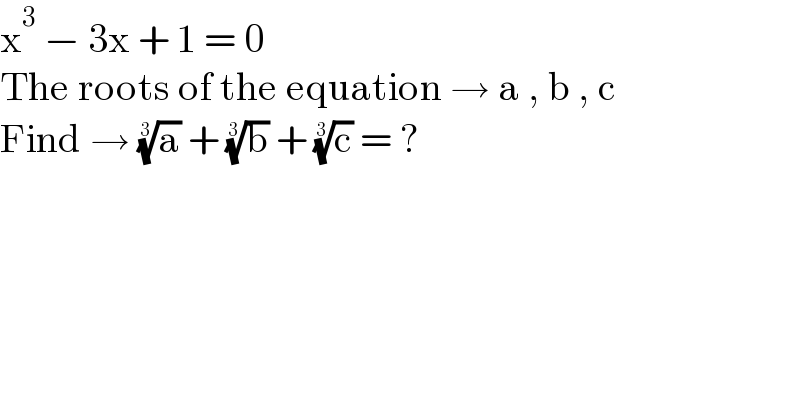
$$\mathrm{x}^{\mathrm{3}} \:−\:\mathrm{3x}\:+\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{The}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\:\rightarrow\:\mathrm{a}\:,\:\mathrm{b}\:,\:\mathrm{c} \\ $$$$\mathrm{Find}\:\rightarrow\:\sqrt[{\mathrm{3}}]{\mathrm{a}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{b}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{c}}\:=\:? \\ $$
Commented by Frix last updated on 24/Mar/25
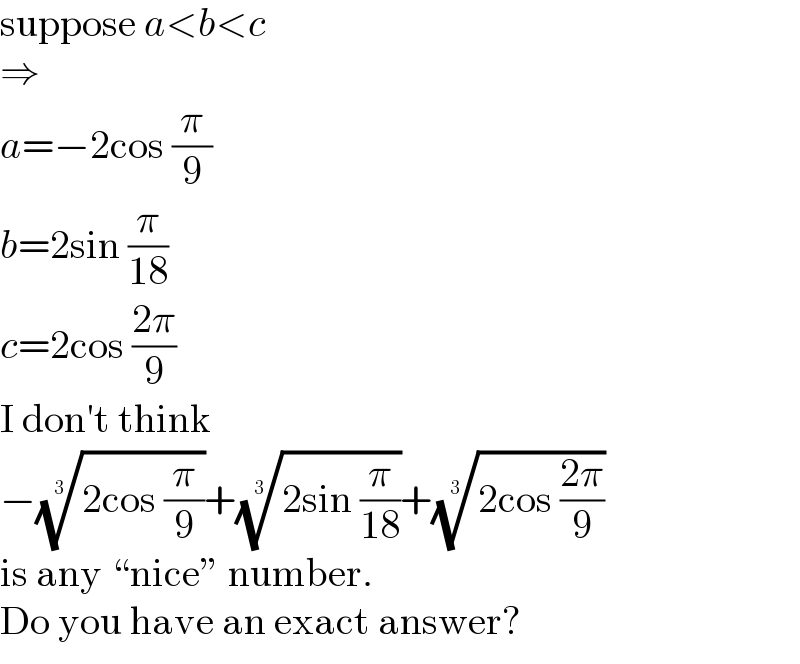
$$\mathrm{suppose}\:{a}<{b}<{c} \\ $$$$\Rightarrow \\ $$$${a}=−\mathrm{2cos}\:\frac{\pi}{\mathrm{9}} \\ $$$${b}=\mathrm{2sin}\:\frac{\pi}{\mathrm{18}} \\ $$$${c}=\mathrm{2cos}\:\frac{\mathrm{2}\pi}{\mathrm{9}} \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think} \\ $$$$−\sqrt[{\mathrm{3}}]{\mathrm{2cos}\:\frac{\pi}{\mathrm{9}}}+\sqrt[{\mathrm{3}}]{\mathrm{2sin}\:\frac{\pi}{\mathrm{18}}}+\sqrt[{\mathrm{3}}]{\mathrm{2cos}\:\frac{\mathrm{2}\pi}{\mathrm{9}}} \\ $$$$\mathrm{is}\:\mathrm{any}\:``\mathrm{nice}''\:\mathrm{number}. \\ $$$$\mathrm{Do}\:\mathrm{you}\:\mathrm{have}\:\mathrm{an}\:\mathrm{exact}\:\mathrm{answer}? \\ $$
Commented by hardmath last updated on 24/Mar/25

$$ \\ $$Dear professor, I don't know the answer
Commented by Ghisom last updated on 26/Mar/25
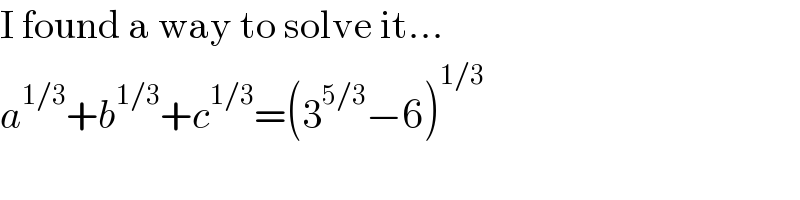
$$\mathrm{I}\:\mathrm{found}\:\mathrm{a}\:\mathrm{way}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{it}... \\ $$$${a}^{\mathrm{1}/\mathrm{3}} +{b}^{\mathrm{1}/\mathrm{3}} +{c}^{\mathrm{1}/\mathrm{3}} =\left(\mathrm{3}^{\mathrm{5}/\mathrm{3}} −\mathrm{6}\right)^{\mathrm{1}/\mathrm{3}} \\ $$
Commented by mr W last updated on 27/Apr/25

$${my}\:{solution}\:{see}\:{Q}\mathrm{219454} \\ $$
