
Question Number 147566 by mathdanisur last updated on 21/Jul/21
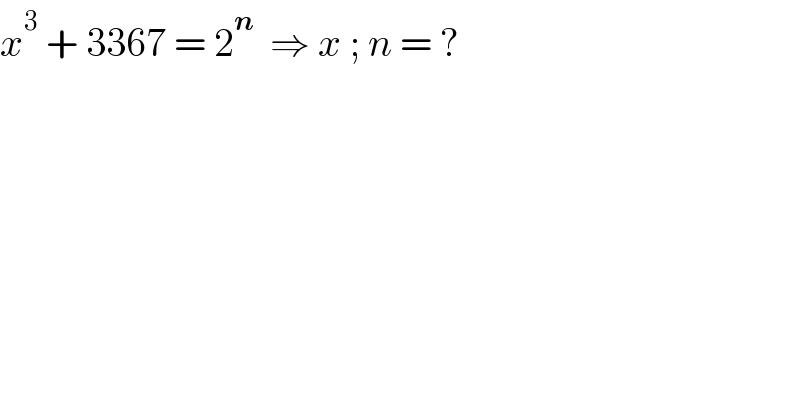
$${x}^{\mathrm{3}} \:+\:\mathrm{3367}\:=\:\mathrm{2}^{\boldsymbol{{n}}} \:\:\Rightarrow\:{x}\:;\:{n}\:=\:? \\ $$
Answered by Olaf_Thorendsen last updated on 21/Jul/21
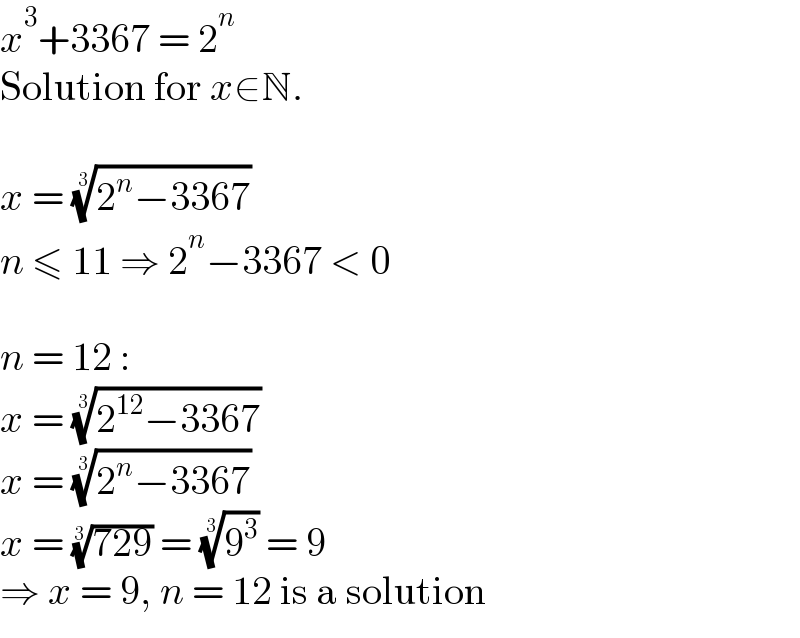
$${x}^{\mathrm{3}} +\mathrm{3367}\:=\:\mathrm{2}^{{n}} \\ $$$$\mathrm{Solution}\:\mathrm{for}\:{x}\in\mathbb{N}. \\ $$$$ \\ $$$${x}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{2}^{{n}} −\mathrm{3367}} \\ $$$${n}\:\leqslant\:\mathrm{11}\:\Rightarrow\:\mathrm{2}^{{n}} −\mathrm{3367}\:<\:\mathrm{0} \\ $$$$ \\ $$$${n}\:=\:\mathrm{12}\:: \\ $$$${x}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{2}^{\mathrm{12}} −\mathrm{3367}} \\ $$$${x}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{2}^{{n}} −\mathrm{3367}} \\ $$$${x}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{729}}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{9}^{\mathrm{3}} }\:=\:\mathrm{9} \\ $$$$\Rightarrow\:{x}\:=\:\mathrm{9},\:{n}\:=\:\mathrm{12}\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution} \\ $$
Commented by mathdanisur last updated on 22/Jul/21

$${thank}\:{you}\:{Sir} \\ $$
