Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 17742 by tawa tawa last updated on 10/Jul/17

x^3 = 3^x , find x.

$$\mathrm{x}^{\mathrm{3}} \:=\:\mathrm{3}^{\mathrm{x}} ,\:\:\:\mathrm{find}\:\mathrm{x}. \\ $$

Commented by 1kanika# last updated on 10/Jul/17

x=3

$$\mathrm{x}=\mathrm{3} \\ $$

Answered by mrW1 last updated on 10/Jul/17

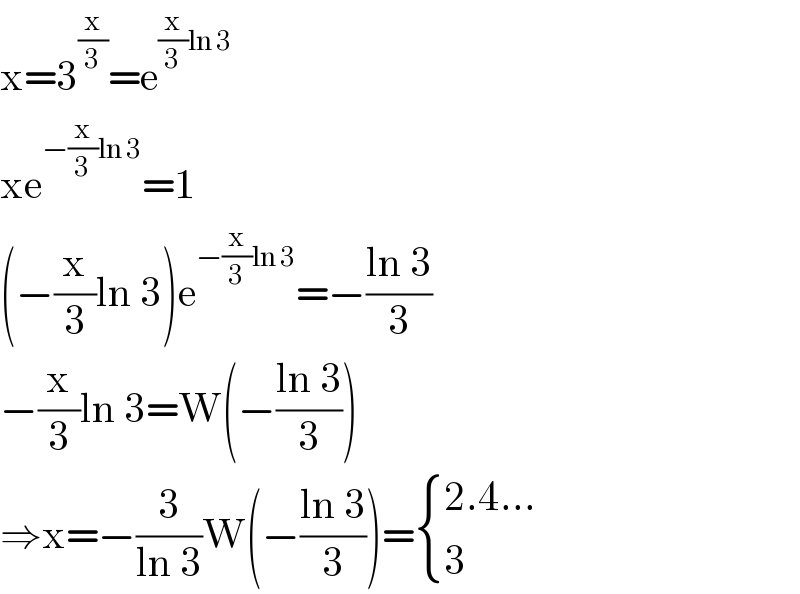
x=3^(x/3) =e^((x/3)ln 3) xe^(−(x/3)ln 3) =1 (−(x/3)ln 3)e^(−(x/3)ln 3) =−((ln 3)/3) −(x/3)ln 3=W(−((ln 3)/3)) ⇒x=−(3/(ln 3))W(−((ln 3)/3))= { ((2.4...)),(3) :}

$$\mathrm{x}=\mathrm{3}^{\frac{\mathrm{x}}{\mathrm{3}}} =\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{3}}\mathrm{ln}\:\mathrm{3}} \\ $$$$\mathrm{xe}^{−\frac{\mathrm{x}}{\mathrm{3}}\mathrm{ln}\:\mathrm{3}} =\mathrm{1} \\ $$$$\left(−\frac{\mathrm{x}}{\mathrm{3}}\mathrm{ln}\:\mathrm{3}\right)\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{3}}\mathrm{ln}\:\mathrm{3}} =−\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{3}} \\ $$$$−\frac{\mathrm{x}}{\mathrm{3}}\mathrm{ln}\:\mathrm{3}=\mathrm{W}\left(−\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{3}}\right) \\ $$$$\Rightarrow\mathrm{x}=−\frac{\mathrm{3}}{\mathrm{ln}\:\mathrm{3}}\mathrm{W}\left(−\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{3}}\right)=\begin{cases}{\mathrm{2}.\mathrm{4}...}\\{\mathrm{3}}\end{cases} \\ $$

Commented by tawa tawa last updated on 10/Jul/17

God bless you sir. i understand it. i really appreciate.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{understand}\:\mathrm{it}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$

Commented by mrW1 last updated on 10/Jul/17

solve x^2 =3^x

$$\mathrm{solve}\:\mathrm{x}^{\mathrm{2}} =\mathrm{3}^{\mathrm{x}} \\ $$

Commented by tawa tawa last updated on 10/Jul/17

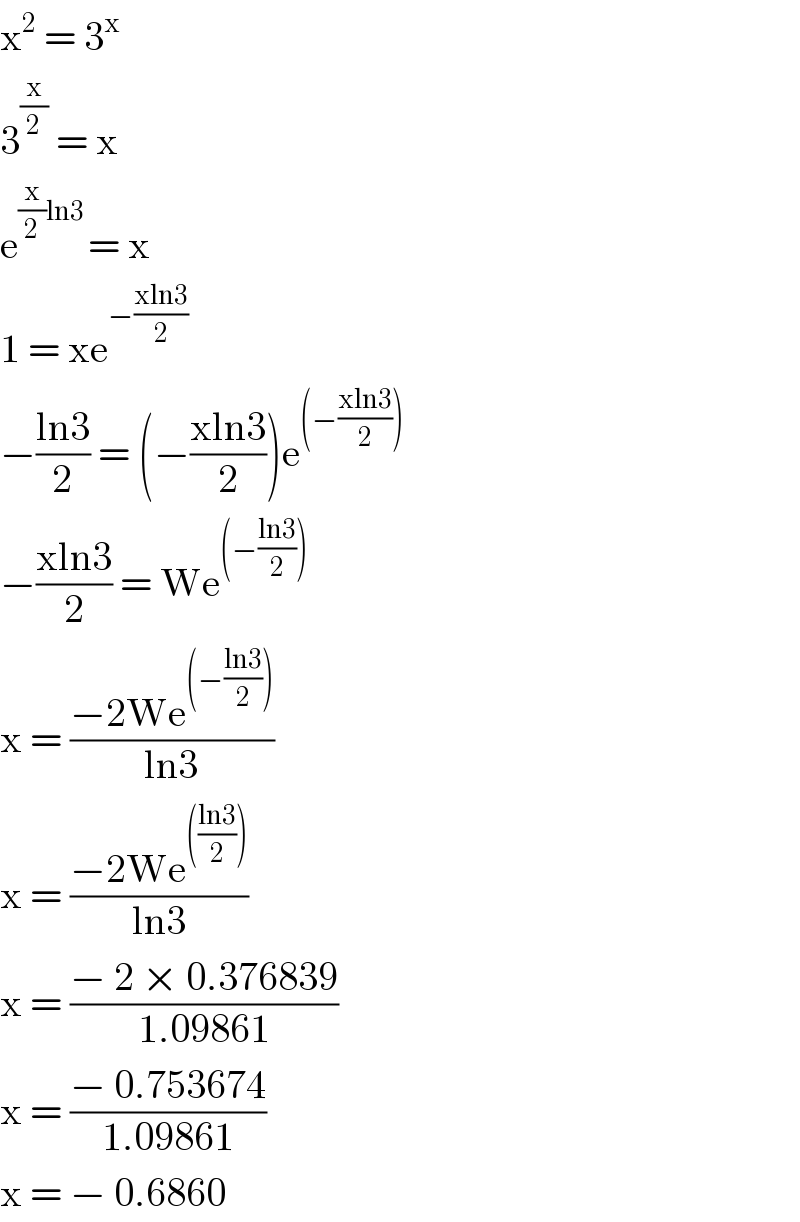
x^2 = 3^x 3^(x/2) = x e^((x/2)ln3 ) = x 1 = xe^(−((xln3)/2)) −((ln3)/2) = (−((xln3)/2))e^((−((xln3)/2))) −((xln3)/2) = We^((−((ln3)/2))) x = ((−2We^((−((ln3)/2))) )/(ln3)) x = ((−2We^((((ln3)/2))) )/(ln3)) x = ((− 2 × 0.376839)/(1.09861)) x = ((− 0.753674)/(1.09861)) x = − 0.6860

$$\mathrm{x}^{\mathrm{2}} \:=\:\mathrm{3}^{\mathrm{x}} \\ $$$$\mathrm{3}^{\frac{\mathrm{x}}{\mathrm{2}}} \:=\:\mathrm{x} \\ $$$$\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}\mathrm{ln3}\:} =\:\mathrm{x} \\ $$$$\mathrm{1}\:=\:\mathrm{xe}^{−\frac{\mathrm{xln3}}{\mathrm{2}}} \\ $$$$−\frac{\mathrm{ln3}}{\mathrm{2}}\:=\:\left(−\frac{\mathrm{xln3}}{\mathrm{2}}\right)\mathrm{e}^{\left(−\frac{\mathrm{xln3}}{\mathrm{2}}\right)} \\ $$$$−\frac{\mathrm{xln3}}{\mathrm{2}}\:=\:\mathrm{We}^{\left(−\frac{\mathrm{ln3}}{\mathrm{2}}\right)} \\ $$$$\mathrm{x}\:=\:\frac{−\mathrm{2We}^{\left(−\frac{\mathrm{ln3}}{\mathrm{2}}\right)} }{\mathrm{ln3}} \\ $$$$\mathrm{x}\:=\:\frac{−\mathrm{2We}^{\left(\frac{\mathrm{ln3}}{\mathrm{2}}\right)} }{\mathrm{ln3}} \\ $$$$\mathrm{x}\:=\:\frac{−\:\mathrm{2}\:×\:\mathrm{0}.\mathrm{376839}}{\mathrm{1}.\mathrm{09861}} \\ $$$$\mathrm{x}\:=\:\frac{−\:\mathrm{0}.\mathrm{753674}}{\mathrm{1}.\mathrm{09861}} \\ $$$$\mathrm{x}\:=\:−\:\mathrm{0}.\mathrm{6860} \\ $$

Commented by mrW1 last updated on 10/Jul/17

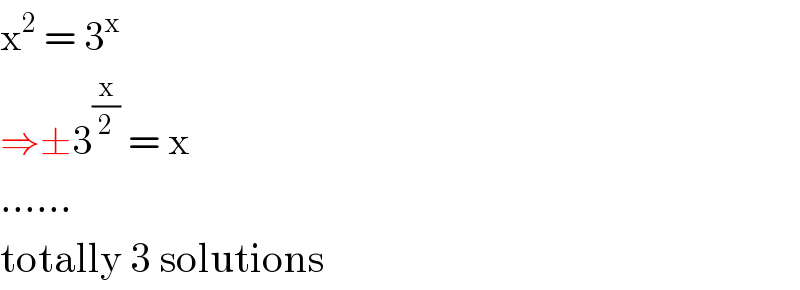
x^2 = 3^x ⇒±3^(x/2) = x ...... totally 3 solutions

$$\mathrm{x}^{\mathrm{2}} \:=\:\mathrm{3}^{\mathrm{x}} \\ $$$$\Rightarrow\pm\mathrm{3}^{\frac{\mathrm{x}}{\mathrm{2}}} \:=\:\mathrm{x} \\ $$$$...... \\ $$$$\mathrm{totally}\:\mathrm{3}\:\mathrm{solutions} \\ $$

Commented by tawa tawa last updated on 10/Jul/17

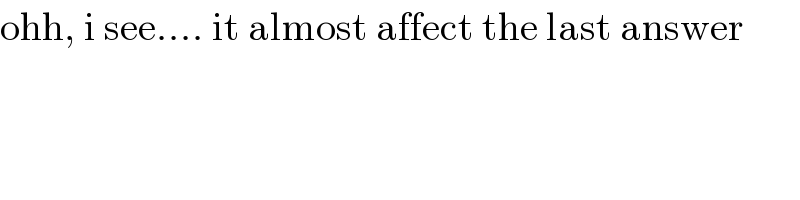
ohh, i see.... it almost affect the last answer

$$\mathrm{ohh},\:\mathrm{i}\:\mathrm{see}....\:\mathrm{it}\:\mathrm{almost}\:\mathrm{affect}\:\mathrm{the}\:\mathrm{last}\:\mathrm{answer} \\ $$

Commented by tawa tawa last updated on 10/Jul/17

Sir.. .. x^3 has two solutions x^2 has three solutions ... or it depends on the question.

$$\mathrm{Sir}..\:..\:\mathrm{x}^{\mathrm{3}} \:\mathrm{has}\:\mathrm{two}\:\mathrm{solutions} \\ $$$$\mathrm{x}^{\mathrm{2}} \:\mathrm{has}\:\mathrm{three}\:\mathrm{solutions}\:... \\ $$$$\mathrm{or}\:\mathrm{it}\:\mathrm{depends}\:\mathrm{on}\:\mathrm{the}\:\mathrm{question}. \\ $$

Commented by tawa tawa last updated on 10/Jul/17

Show me sir.

$$\mathrm{Show}\:\mathrm{me}\:\mathrm{sir}. \\ $$

Commented by mrW1 last updated on 10/Jul/17

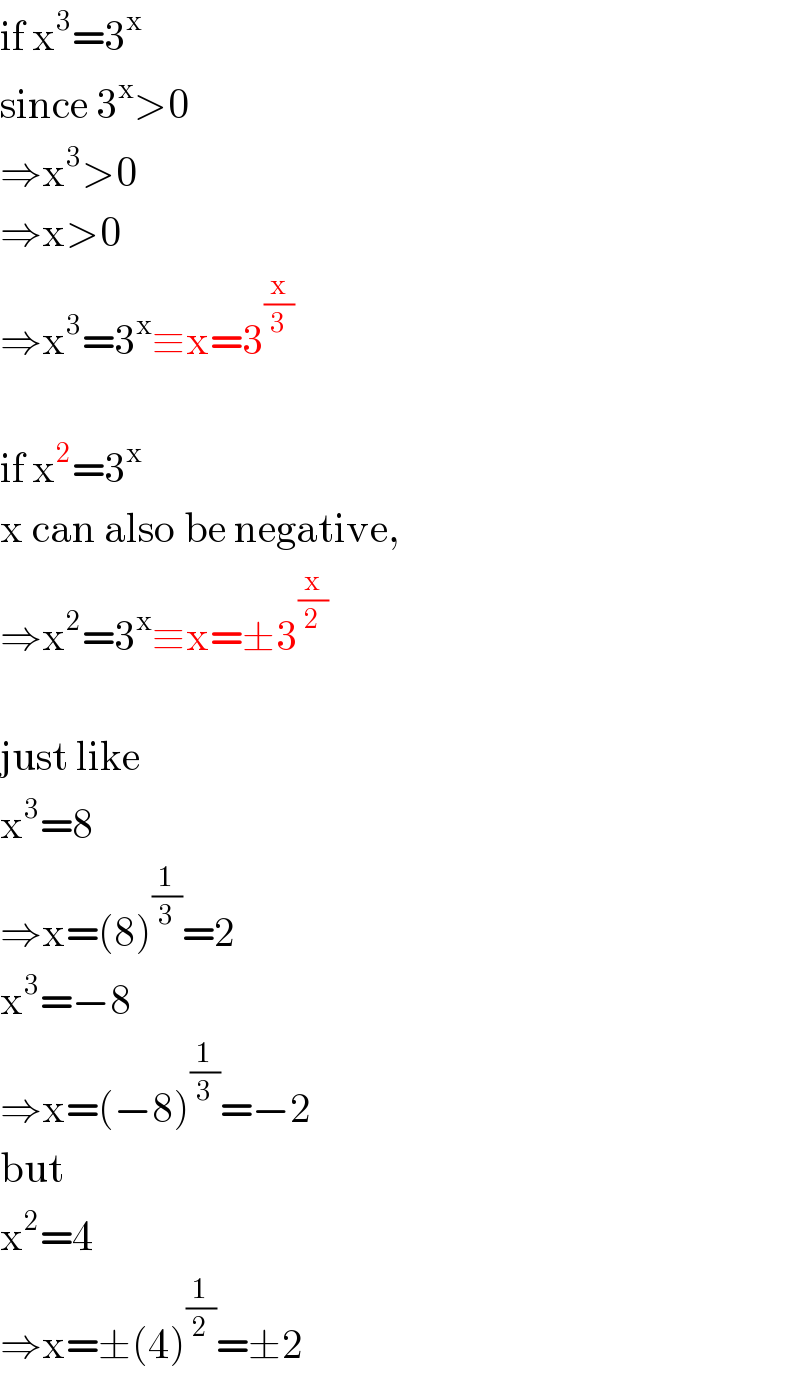
if x^3 =3^x since 3^x >0 ⇒x^3 >0 ⇒x>0 ⇒x^3 =3^x ≡x=3^(x/3) if x^2 =3^x x can also be negative, ⇒x^2 =3^x ≡x=±3^(x/2) just like x^3 =8 ⇒x=(8)^(1/3) =2 x^3 =−8 ⇒x=(−8)^(1/3) =−2 but x^2 =4 ⇒x=±(4)^(1/2) =±2

$$\mathrm{if}\:\mathrm{x}^{\mathrm{3}} =\mathrm{3}^{\mathrm{x}} \\ $$$$\mathrm{since}\:\mathrm{3}^{\mathrm{x}} >\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{3}} >\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}>\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{3}} =\mathrm{3}^{\mathrm{x}} \equiv\mathrm{x}=\mathrm{3}^{\frac{\mathrm{x}}{\mathrm{3}}} \\ $$$$ \\ $$$$\mathrm{if}\:\mathrm{x}^{\mathrm{2}} =\mathrm{3}^{\mathrm{x}} \\ $$$$\mathrm{x}\:\mathrm{can}\:\mathrm{also}\:\mathrm{be}\:\mathrm{negative}, \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} =\mathrm{3}^{\mathrm{x}} \equiv\mathrm{x}=\pm\mathrm{3}^{\frac{\mathrm{x}}{\mathrm{2}}} \\ $$$$ \\ $$$$\mathrm{just}\:\mathrm{like} \\ $$$$\mathrm{x}^{\mathrm{3}} =\mathrm{8} \\ $$$$\Rightarrow\mathrm{x}=\left(\mathrm{8}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =\mathrm{2} \\ $$$$\mathrm{x}^{\mathrm{3}} =−\mathrm{8} \\ $$$$\Rightarrow\mathrm{x}=\left(−\mathrm{8}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =−\mathrm{2} \\ $$$$\mathrm{but} \\ $$$$\mathrm{x}^{\mathrm{2}} =\mathrm{4} \\ $$$$\Rightarrow\mathrm{x}=\pm\left(\mathrm{4}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\pm\mathrm{2} \\ $$

Commented by tawa tawa last updated on 10/Jul/17

Now, i understand sir. God bless you

$$\mathrm{Now},\:\mathrm{i}\:\mathrm{understand}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$

Commented by mrW1 last updated on 10/Jul/17

solution for x^4 =3^x x=±3^(x/4) x=±e^((x/4)ln 3) xe^(−(x/4)ln 3) =±1 (−(x/4)ln 3)e^(−(x/4)ln 3) =±((ln 3)/4) −(x/4)ln 3=W(±((ln 3)/4)) ⇒x=−(4/(ln 3))W(±((ln 3)/4)) x= { ((−(4/(ln 3)) W(((ln 3)/4))=−0.80225)),((−(4/(ln 3)) W(−((ln 3)/4))= { ((1.51687)),((7.17476)) :})) :}

$$\mathrm{solution}\:\mathrm{for}\:\mathrm{x}^{\mathrm{4}} =\mathrm{3}^{\mathrm{x}} \\ $$$$\mathrm{x}=\pm\mathrm{3}^{\frac{\mathrm{x}}{\mathrm{4}}} \\ $$$$\mathrm{x}=\pm\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{4}}\mathrm{ln}\:\mathrm{3}} \\ $$$$\mathrm{xe}^{−\frac{\mathrm{x}}{\mathrm{4}}\mathrm{ln}\:\mathrm{3}} =\pm\mathrm{1} \\ $$$$\left(−\frac{\mathrm{x}}{\mathrm{4}}\mathrm{ln}\:\mathrm{3}\right)\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{4}}\mathrm{ln}\:\mathrm{3}} =\pm\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{4}} \\ $$$$−\frac{\mathrm{x}}{\mathrm{4}}\mathrm{ln}\:\mathrm{3}=\mathrm{W}\left(\pm\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{4}}\right) \\ $$$$\Rightarrow\mathrm{x}=−\frac{\mathrm{4}}{\mathrm{ln}\:\mathrm{3}}\mathrm{W}\left(\pm\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{4}}\right) \\ $$$$\mathrm{x}=\begin{cases}{−\frac{\mathrm{4}}{\mathrm{ln}\:\mathrm{3}}\:\mathrm{W}\left(\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{4}}\right)=−\mathrm{0}.\mathrm{80225}}\\{−\frac{\mathrm{4}}{\mathrm{ln}\:\mathrm{3}}\:\mathrm{W}\left(−\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{4}}\right)=\begin{cases}{\mathrm{1}.\mathrm{51687}}\\{\mathrm{7}.\mathrm{17476}}\end{cases}}\end{cases} \\ $$

Commented by tawa tawa last updated on 10/Jul/17

I really appreciate your effort sir. God bless you sir.

$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com