Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 207434 by Frix last updated on 15/May/24

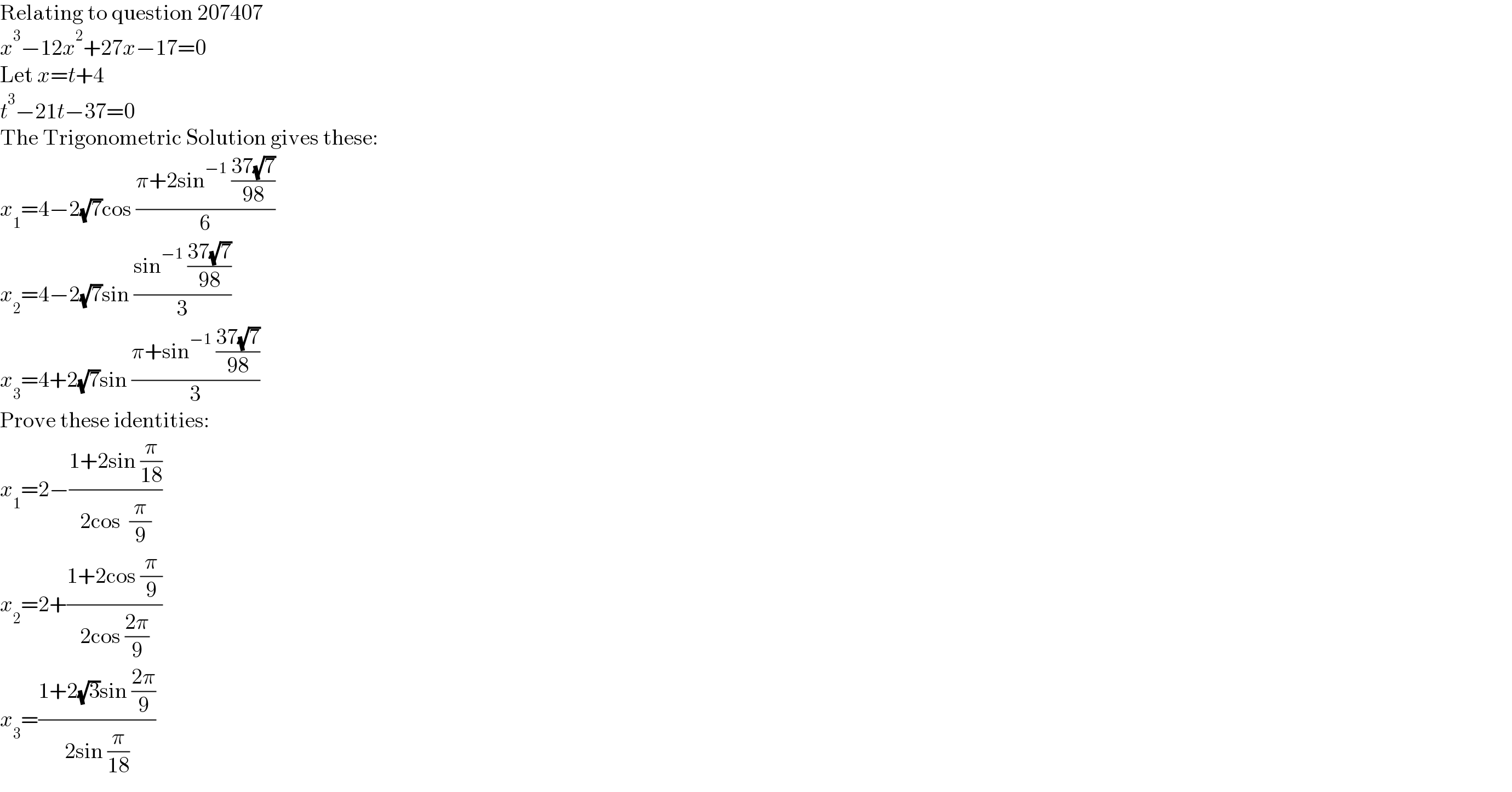
x^3 −12x^2 +27x−17=0 Let x=t+4 t^3 −21t−37=0 The Trigonometric Solution gives these: x_1 =4−2(√7)cos ((π+2sin^(−1) ((37(√7))/(98)))/6) x_2 =4−2(√7)sin ((sin^(−1) ((37(√7))/(98)))/3) x_3 =4+2(√7)sin ((π+sin^(−1) ((37(√7))/(98)))/3) Prove these identities: x_1 =2−((1+2sin (π/(18)))/(2cos (π/9))) x_2 =2+((1+2cos (π/9))/(2cos ((2π)/9))) x_3 =((1+2(√3)sin ((2π)/9))/(2sin (π/(18))))

$${x}^{\mathrm{3}} −\mathrm{12}{x}^{\mathrm{2}} +\mathrm{27}{x}−\mathrm{17}=\mathrm{0} \\ $$$$\mathrm{Let}\:{x}={t}+\mathrm{4} \\ $$$${t}^{\mathrm{3}} −\mathrm{21}{t}−\mathrm{37}=\mathrm{0} \\ $$$$\mathrm{The}\:\mathrm{Trigonometric}\:\mathrm{Solution}\:\mathrm{gives}\:\mathrm{these}: \\ $$$${x}_{\mathrm{1}} =\mathrm{4}−\mathrm{2}\sqrt{\mathrm{7}}\mathrm{cos}\:\frac{\pi+\mathrm{2sin}^{−\mathrm{1}} \:\frac{\mathrm{37}\sqrt{\mathrm{7}}}{\mathrm{98}}}{\mathrm{6}} \\ $$$${x}_{\mathrm{2}} =\mathrm{4}−\mathrm{2}\sqrt{\mathrm{7}}\mathrm{sin}\:\frac{\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{37}\sqrt{\mathrm{7}}}{\mathrm{98}}}{\mathrm{3}} \\ $$$${x}_{\mathrm{3}} =\mathrm{4}+\mathrm{2}\sqrt{\mathrm{7}}\mathrm{sin}\:\frac{\pi+\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{37}\sqrt{\mathrm{7}}}{\mathrm{98}}}{\mathrm{3}} \\ $$$$\mathrm{Prove}\:\mathrm{these}\:\mathrm{identities}: \\ $$$${x}_{\mathrm{1}} =\mathrm{2}−\frac{\mathrm{1}+\mathrm{2sin}\:\frac{\pi}{\mathrm{18}}}{\mathrm{2cos}\:\:\frac{\pi}{\mathrm{9}}} \\ $$$${x}_{\mathrm{2}} =\mathrm{2}+\frac{\mathrm{1}+\mathrm{2cos}\:\frac{\pi}{\mathrm{9}}}{\mathrm{2cos}\:\frac{\mathrm{2}\pi}{\mathrm{9}}} \\ $$$${x}_{\mathrm{3}} =\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{9}}}{\mathrm{2sin}\:\frac{\pi}{\mathrm{18}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com