
Question Number 191640 by vishal1234 last updated on 28/Apr/23
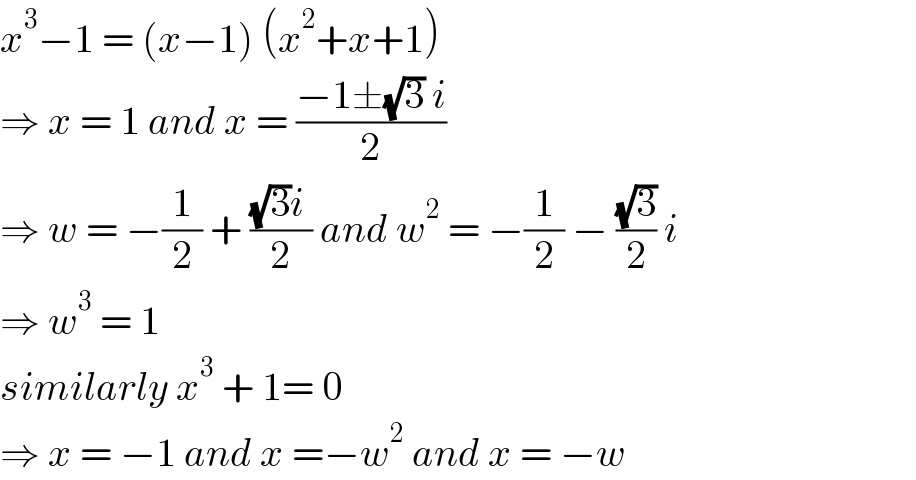
$${x}^{\mathrm{3}} −\mathrm{1}\:=\:\left({x}−\mathrm{1}\right)\:\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right) \\ $$$$\Rightarrow\:{x}\:=\:\mathrm{1}\:{and}\:{x}\:=\:\frac{−\mathrm{1}\pm\sqrt{\mathrm{3}}\:{i}}{\mathrm{2}} \\ $$$$\Rightarrow\:{w}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\sqrt{\mathrm{3}}{i}\:}{\mathrm{2}}\:{and}\:{w}^{\mathrm{2}} \:=\:−\frac{\mathrm{1}}{\mathrm{2}}\:−\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{i} \\ $$$$\Rightarrow\:{w}^{\mathrm{3}} \:=\:\mathrm{1} \\ $$$${similarly}\:{x}^{\mathrm{3}} \:+\:\mathrm{1}=\:\mathrm{0} \\ $$$$\Rightarrow\:{x}\:=\:−\mathrm{1}\:{and}\:{x}\:=−{w}^{\mathrm{2}} \:{and}\:{x}\:=\:−{w} \\ $$
Commented by a.lgnaoui last updated on 28/Apr/23
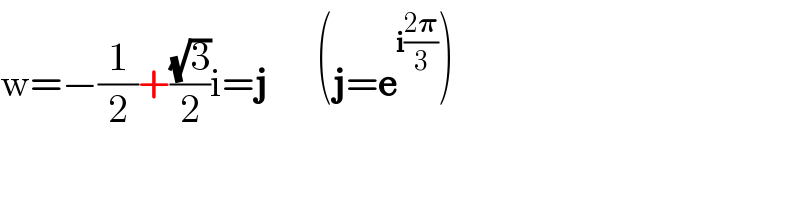
$$\mathrm{w}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}=\boldsymbol{\mathrm{j}}\:\:\:\:\:\:\left(\boldsymbol{\mathrm{j}}=\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{i}}\frac{\mathrm{2}\boldsymbol{\pi}}{\mathrm{3}}} \right) \\ $$
