Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 140669 by john_santu last updated on 11/May/21

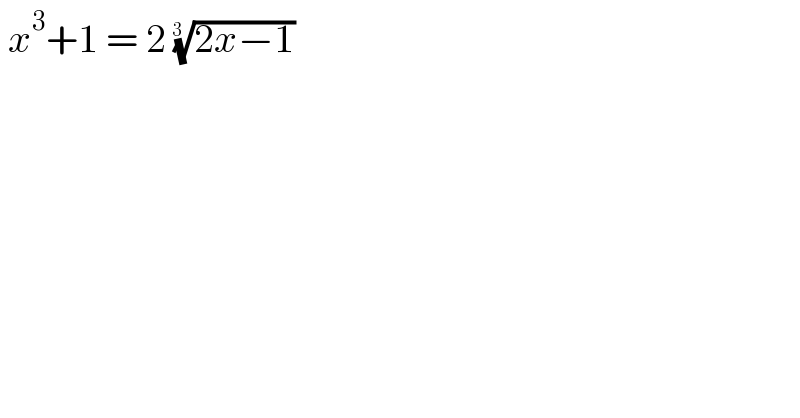
x^3 +1 = 2 ((2x−1))^(1/(3 ))

$$\:{x}^{\mathrm{3}} +\mathrm{1}\:=\:\mathrm{2}\:\sqrt[{\mathrm{3}\:}]{\mathrm{2}{x}−\mathrm{1}} \\ $$

Answered by bemath last updated on 11/May/21

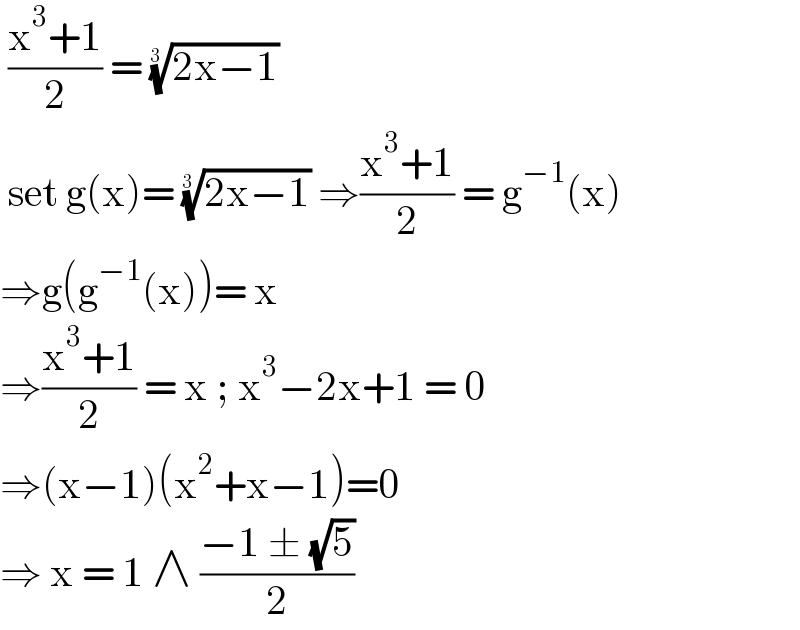
((x^3 +1)/2) = ((2x−1))^(1/(3 )) set g(x)= ((2x−1))^(1/(3 )) ⇒((x^3 +1)/2) = g^(−1) (x) ⇒g(g^(−1) (x))= x ⇒((x^3 +1)/2) = x ; x^3 −2x+1 = 0 ⇒(x−1)(x^2 +x−1)=0 ⇒ x = 1 ∧ ((−1 ± (√5))/2)

$$\:\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{1}}{\mathrm{2}}\:=\:\sqrt[{\mathrm{3}\:}]{\mathrm{2x}−\mathrm{1}} \\ $$$$\:\mathrm{set}\:\mathrm{g}\left(\mathrm{x}\right)=\:\sqrt[{\mathrm{3}\:}]{\mathrm{2x}−\mathrm{1}}\:\Rightarrow\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{1}}{\mathrm{2}}\:=\:\mathrm{g}^{−\mathrm{1}} \left(\mathrm{x}\right) \\ $$$$\Rightarrow\mathrm{g}\left(\mathrm{g}^{−\mathrm{1}} \left(\mathrm{x}\right)\right)=\:\mathrm{x}\: \\ $$$$\Rightarrow\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{1}}{\mathrm{2}}\:=\:\mathrm{x}\:;\:\mathrm{x}^{\mathrm{3}} −\mathrm{2x}+\mathrm{1}\:=\:\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{x}\:=\:\mathrm{1}\:\wedge\:\frac{−\mathrm{1}\:\pm\:\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com