Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 7814 by Tawakalitu. last updated on 16/Sep/16

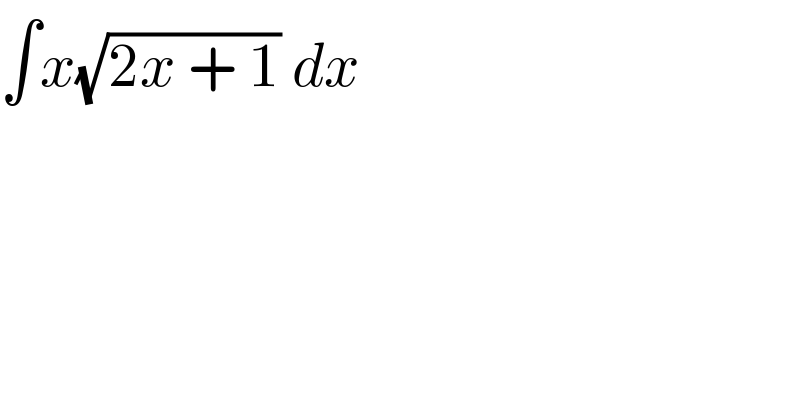
∫x(√(2x + 1)) dx

$$\int{x}\sqrt{\mathrm{2}{x}\:+\:\mathrm{1}}\:{dx}\: \\ $$

Commented by l-becker last updated on 17/Sep/16

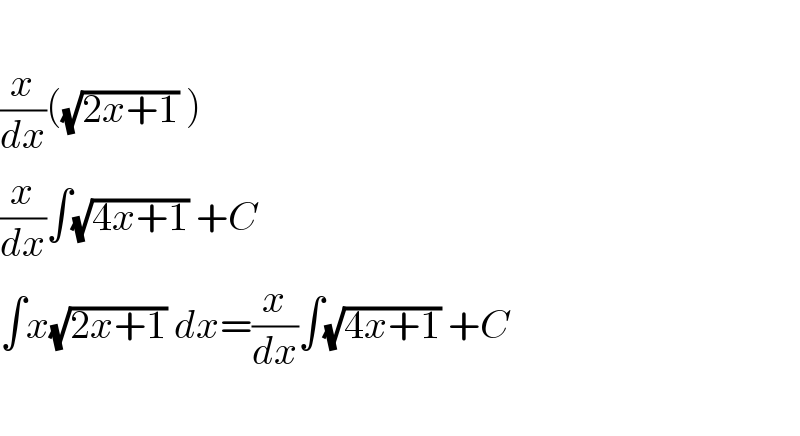
(x/dx)((√(2x+1)) ) (x/dx)∫(√(4x+1)) +C ∫x(√(2x+1)) dx=(x/dx)∫(√(4x+1)) +C

$$ \\ $$$$\frac{{x}}{{dx}}\left(\sqrt{\mathrm{2}{x}+\mathrm{1}}\:\right) \\ $$$$\frac{{x}}{{dx}}\int\sqrt{\mathrm{4}{x}+\mathrm{1}}\:+{C} \\ $$$$\int{x}\sqrt{\mathrm{2}{x}+\mathrm{1}}\:{dx}=\frac{{x}}{{dx}}\int\sqrt{\mathrm{4}{x}+\mathrm{1}}\:+{C} \\ $$$$ \\ $$

Commented by ridwan balatif last updated on 17/Sep/16

derivative ∣ integral x ∣ (2x+1)^(1/2) −−−−−−−−−−−−−−−− 1 ∣ (2/3)(2x+1)^(3/2) ((1/2))=(1/3)(2x+1)^(3/2) .(+1) 0 ∣ (1/3).(2/5)(2x+1)^(5/2) ((1/2))=(1/(15))(2x+1)^(5/2) .(−1) ∫x(√(2x+1))dx=(1/3)x(2x+1)^(3/2) −(1/(15))(2x+1)^(5/2) +C ∫x(√(2x+1))dx=(1/(15))(2x+1)^(3/2) (3x−1)+C i use tanzalin ways

$${derivative}\:\:\:\:\:\:\:\mid\:\:\:{integral} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:\left(\mathrm{2}{x}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$−−−−−−−−−−−−−−−− \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:\:\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{2}{x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}{x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\:\:\:\:\:\:\:.\left(+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:\:\frac{\mathrm{1}}{\mathrm{3}}.\frac{\mathrm{2}}{\mathrm{5}}\left(\mathrm{2}{x}+\mathrm{1}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{15}}\left(\mathrm{2}{x}+\mathrm{1}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} \:\:\:\:\:\:\:\:\:.\left(−\mathrm{1}\right) \\ $$$$\int{x}\sqrt{\mathrm{2}{x}+\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{3}}{x}\left(\mathrm{2}{x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{15}}\left(\mathrm{2}{x}+\mathrm{1}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} +{C} \\ $$$$\int{x}\sqrt{\mathrm{2}{x}+\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{15}}\left(\mathrm{2}{x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{3}{x}−\mathrm{1}\right)+{C} \\ $$$${i}\:{use}\:{tanzalin}\:{ways} \\ $$

Commented by FilupSmith last updated on 17/Sep/16

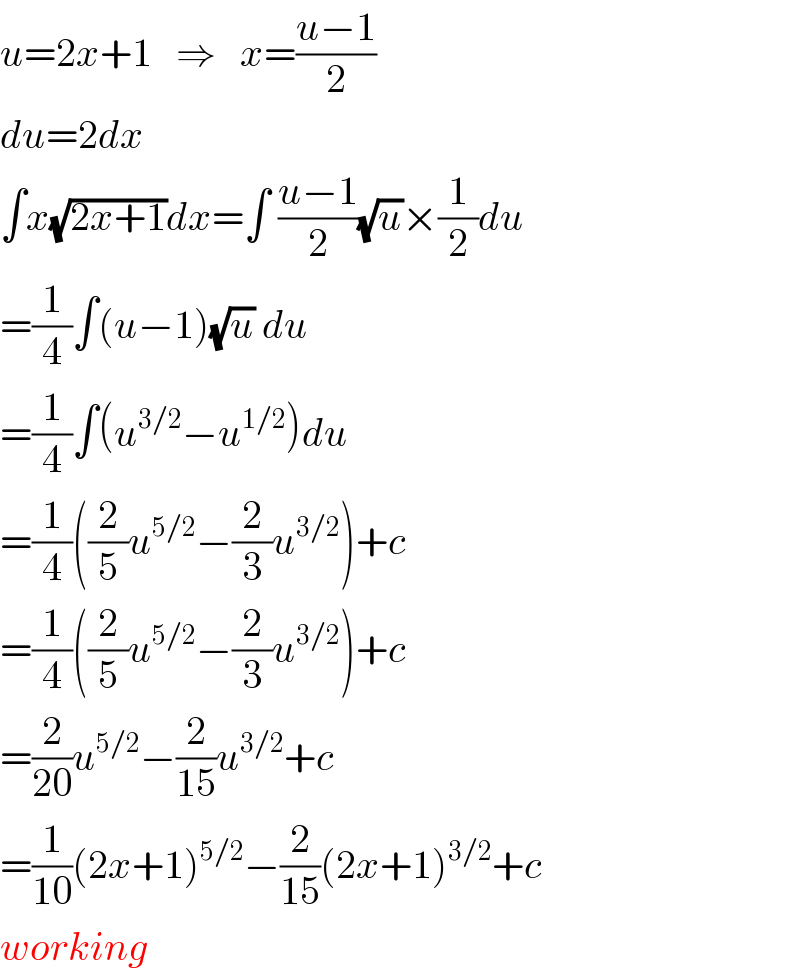
u=2x+1 ⇒ x=((u−1)/2) du=2dx ∫x(√(2x+1))dx=∫ ((u−1)/2)(√u)×(1/2)du =(1/4)∫(u−1)(√u) du =(1/4)∫(u^(3/2) −u^(1/2) )du =(1/4)((2/5)u^(5/2) −(2/3)u^(3/2) )+c =(1/4)((2/5)u^(5/2) −(2/3)u^(3/2) )+c =(2/(20))u^(5/2) −(2/(15))u^(3/2) +c =(1/(10))(2x+1)^(5/2) −(2/(15))(2x+1)^(3/2) +c working

$${u}=\mathrm{2}{x}+\mathrm{1}\:\:\:\Rightarrow\:\:\:{x}=\frac{{u}−\mathrm{1}}{\mathrm{2}} \\ $$$${du}=\mathrm{2}{dx} \\ $$$$\int{x}\sqrt{\mathrm{2}{x}+\mathrm{1}}{dx}=\int\:\frac{{u}−\mathrm{1}}{\mathrm{2}}\sqrt{{u}}×\frac{\mathrm{1}}{\mathrm{2}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\left({u}−\mathrm{1}\right)\sqrt{{u}}\:{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\left({u}^{\mathrm{3}/\mathrm{2}} −{u}^{\mathrm{1}/\mathrm{2}} \right){du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{2}}{\mathrm{5}}{u}^{\mathrm{5}/\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}{u}^{\mathrm{3}/\mathrm{2}} \right)+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{2}}{\mathrm{5}}{u}^{\mathrm{5}/\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}{u}^{\mathrm{3}/\mathrm{2}} \right)+{c} \\ $$$$=\frac{\mathrm{2}}{\mathrm{20}}{u}^{\mathrm{5}/\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{15}}{u}^{\mathrm{3}/\mathrm{2}} +{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{5}/\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{15}}\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} +{c} \\ $$$${working} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com