Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 177193 by peter frank last updated on 02/Oct/22

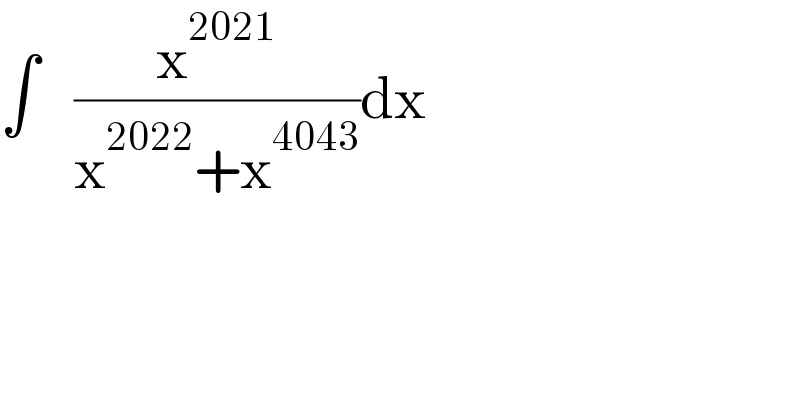
∫ (x^(2021) /(x^(2022) +x^(4043) ))dx

$$\int\:\:\:\frac{\mathrm{x}^{\mathrm{2021}} }{\mathrm{x}^{\mathrm{2022}} +\mathrm{x}^{\mathrm{4043}} }\mathrm{dx} \\ $$

Answered by cortano1 last updated on 02/Oct/22

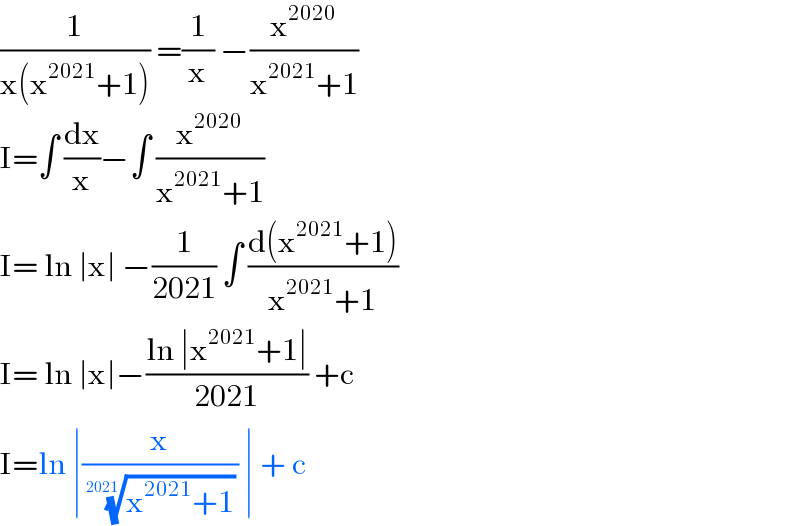
(1/(x(x^(2021) +1))) =(1/x) −(x^(2020) /(x^(2021) +1)) I=∫ (dx/x)−∫ (x^(2020) /(x^(2021) +1)) I= ln ∣x∣ −(1/(2021)) ∫ ((d(x^(2021) +1))/(x^(2021) +1)) I= ln ∣x∣−((ln ∣x^(2021) +1∣)/(2021)) +c I=ln ∣(x/( ((x^(2021) +1))^(1/(2021)) )) ∣ + c

$$\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2021}} +\mathrm{1}\right)}\:=\frac{\mathrm{1}}{\mathrm{x}}\:−\frac{\mathrm{x}^{\mathrm{2020}} }{\mathrm{x}^{\mathrm{2021}} +\mathrm{1}} \\ $$$$\mathrm{I}=\int\:\frac{\mathrm{dx}}{\mathrm{x}}−\int\:\frac{\mathrm{x}^{\mathrm{2020}} }{\mathrm{x}^{\mathrm{2021}} +\mathrm{1}} \\ $$$$\mathrm{I}=\:\mathrm{ln}\:\mid\mathrm{x}\mid\:−\frac{\mathrm{1}}{\mathrm{2021}}\:\int\:\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{2021}} +\mathrm{1}\right)}{\mathrm{x}^{\mathrm{2021}} +\mathrm{1}} \\ $$$$\mathrm{I}=\:\mathrm{ln}\:\mid\mathrm{x}\mid−\frac{\mathrm{ln}\:\mid\mathrm{x}^{\mathrm{2021}} +\mathrm{1}\mid}{\mathrm{2021}}\:+\mathrm{c}\: \\ $$$$\mathrm{I}=\mathrm{ln}\:\mid\frac{\mathrm{x}}{\:\sqrt[{\mathrm{2021}}]{\mathrm{x}^{\mathrm{2021}} +\mathrm{1}}}\:\mid\:+\:\mathrm{c}\: \\ $$

Commented by peter frank last updated on 02/Oct/22

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by som(math1967) last updated on 02/Oct/22

∫(x^(2021) /(x^(2022) (1+x^(2021) )))dx ∫(dx/(x(1+x^(2021) ))) ∫((x^(2020) dx)/(x^(2021) (1+x^(2021) ))) let x^(2021) =t⇒x^(2020) dx=(dt/(2021)) (1/(2021))∫(dt/(t(t+1))) =(1/(2021))∫(dt/t)−(1/(2021))∫(dt/(t+1)) =(1/(2021))[lnt−ln∣t+1∣] +C =(1/(2021))ln∣(x^(2021) /(x^(2021) +1))∣ +C

$$\int\frac{{x}^{\mathrm{2021}} }{{x}^{\mathrm{2022}} \left(\mathrm{1}+{x}^{\mathrm{2021}} \right)}{dx} \\ $$$$\int\frac{{dx}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2021}} \right)} \\ $$$$\int\frac{{x}^{\mathrm{2020}} {dx}}{{x}^{\mathrm{2021}} \left(\mathrm{1}+{x}^{\mathrm{2021}} \right)} \\ $$$${let}\:{x}^{\mathrm{2021}} ={t}\Rightarrow{x}^{\mathrm{2020}} {dx}=\frac{{dt}}{\mathrm{2021}} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2021}}\int\frac{{dt}}{{t}\left({t}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2021}}\int\frac{{dt}}{{t}}−\frac{\mathrm{1}}{\mathrm{2021}}\int\frac{{dt}}{{t}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2021}}\left[{lnt}−{ln}\mid{t}+\mathrm{1}\mid\right]\:+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2021}}{ln}\mid\frac{{x}^{\mathrm{2021}} }{{x}^{\mathrm{2021}} +\mathrm{1}}\mid\:+{C} \\ $$$$\:\: \\ $$

Commented by peter frank last updated on 02/Oct/22

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com