
Question Number 48725 by Tawa1 last updated on 27/Nov/18
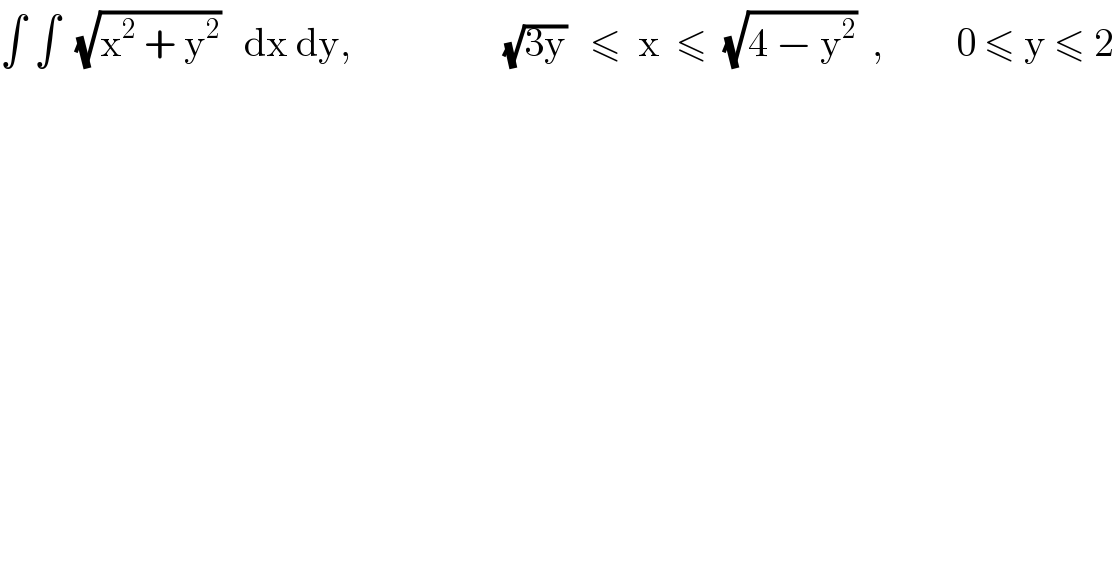
$$\int\:\int\:\:\sqrt{\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{y}^{\mathrm{2}} }\:\:\:\mathrm{dx}\:\mathrm{dy},\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{\mathrm{3y}}\:\:\:\leqslant\:\:\mathrm{x}\:\:\leqslant\:\:\sqrt{\mathrm{4}\:−\:\mathrm{y}^{\mathrm{2}} }\:\:,\:\:\:\:\:\:\:\:\:\mathrm{0}\:\leqslant\:\mathrm{y}\:\leqslant\:\mathrm{2} \\ $$
Commented by Abdo msup. last updated on 27/Nov/18
![let I =∫∫_D (√(x^2 +y^2 ))dxdy with D={(x,y)∈R^2 /0≤y≤2 and (√(3y))≤x≤(√(4−y^2 )) I =∫_0 ^2 (∫_(√(3y)) ^(√(4−y^2 )) (√(x^2 +y^2 ))dx)dy let find A(y)=∫_(√(3y)) ^(√(4−y^2 )) (√(x^2 +y^2 ))dx A(y) =_(x=ysh(t)) ∫_(argsh(((√3)/(√y)))) ^(argsh(((√(4−y^2 ))/y))) ych(t)y ch(t)dt = y^2 ∫_(ln(((√3)/(√y)) +(√(3/y^2 ))+1)) ^(ln(((√(4−y^2 ))/y) +(√((4−y^2 )/y^2 ))+1)) ((1+ch(2t))/2) dt =(y^2 /2){ln(((√(4−y^2 ))/y)+(2/y))−ln(((√3)/(√y)) +(√(3/y^2 ))+1)} +(y^2 /4)[sh(2t)]_(α(y)) ^(β(y)) =...+(y^2 /8)[ e^(2t) −e^(−2t) ]_(α(y)) ^(β(y)) =....+(y^2 /8){ (((√(4−y^2 ))/y) +(2/y))^2 −(((√3)/(√y)) +(√((3/y^2 )+1)))^(−2) } ⇒ A(y)=(y^2 /2){ln(((√(4−y^2 ))/y) +(2/y))−ln(((√3)/(√y)) +(√((3/y^2 )+1))) +(y^2 /8){ln(((√(4−y^2 ))/y) +(2/y))−ln(((√3)/(√y)) +(√((3/y^2 )+1)))^(−2) } ⇒ I =∫_0 ^2 A(y)dy ...be continued...](Q48728.png)
$${let}\:{I}\:=\int\int_{{D}} \:\:\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }{dxdy}\:\:\:{with}\:{D}=\left\{\left({x},{y}\right)\in{R}^{\mathrm{2}} /\mathrm{0}\leqslant{y}\leqslant\mathrm{2}\:{and}\right. \\ $$$$\sqrt{\mathrm{3}{y}}\leqslant{x}\leqslant\sqrt{\mathrm{4}−{y}^{\mathrm{2}} } \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \:\left(\int_{\sqrt{\mathrm{3}{y}}} ^{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }} \sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }{dx}\right){dy}\:{let}\:{find}\:{A}\left({y}\right)=\int_{\sqrt{\mathrm{3}{y}}} ^{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }} \:\:\:\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }{dx} \\ $$$${A}\left({y}\right)\:=_{{x}={ysh}\left({t}\right)} \:\:\:\int_{{argsh}\left(\frac{\sqrt{\mathrm{3}}}{\sqrt{{y}}}\right)} ^{{argsh}\left(\frac{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }}{{y}}\right)} {ych}\left({t}\right){y}\:{ch}\left({t}\right){dt} \\ $$$$=\:{y}^{\mathrm{2}} \int_{{ln}\left(\frac{\sqrt{\mathrm{3}}}{\sqrt{{y}}}\:+\sqrt{\frac{\mathrm{3}}{{y}^{\mathrm{2}} }}+\mathrm{1}\right)} ^{{ln}\left(\frac{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }}{{y}}\:+\sqrt{\frac{\mathrm{4}−{y}^{\mathrm{2}} }{{y}^{\mathrm{2}} }}+\mathrm{1}\right)} \frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\:{dt} \\ $$$$=\frac{{y}^{\mathrm{2}} }{\mathrm{2}}\left\{{ln}\left(\frac{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }}{{y}}+\frac{\mathrm{2}}{{y}}\right)−{ln}\left(\frac{\sqrt{\mathrm{3}}}{\sqrt{{y}}}\:+\sqrt{\frac{\mathrm{3}}{{y}^{\mathrm{2}} }}+\mathrm{1}\right)\right\} \\ $$$$+\frac{{y}^{\mathrm{2}} }{\mathrm{4}}\left[{sh}\left(\mathrm{2}{t}\right)\right]_{\alpha\left({y}\right)} ^{\beta\left({y}\right)} \:=...+\frac{{y}^{\mathrm{2}} }{\mathrm{8}}\left[\:{e}^{\mathrm{2}{t}} −{e}^{−\mathrm{2}{t}} \right]_{\alpha\left({y}\right)} ^{\beta\left({y}\right)} \\ $$$$=....+\frac{{y}^{\mathrm{2}} }{\mathrm{8}}\left\{\:\left(\frac{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }}{{y}}\:+\frac{\mathrm{2}}{{y}}\right)^{\mathrm{2}} \:−\left(\frac{\sqrt{\mathrm{3}}}{\sqrt{{y}}}\:+\sqrt{\frac{\mathrm{3}}{{y}^{\mathrm{2}} }+\mathrm{1}}\right)^{−\mathrm{2}} \right\}\:\Rightarrow \\ $$$${A}\left({y}\right)=\frac{{y}^{\mathrm{2}} }{\mathrm{2}}\left\{{ln}\left(\frac{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }}{{y}}\:+\frac{\mathrm{2}}{{y}}\right)−{ln}\left(\frac{\sqrt{\mathrm{3}}}{\sqrt{{y}}}\:+\sqrt{\frac{\mathrm{3}}{{y}^{\mathrm{2}} }+\mathrm{1}}\right)\right. \\ $$$$+\frac{{y}^{\mathrm{2}} }{\mathrm{8}}\left\{{ln}\left(\frac{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }}{{y}}\:+\frac{\mathrm{2}}{{y}}\right)−{ln}\left(\frac{\sqrt{\mathrm{3}}}{\sqrt{{y}}}\:+\sqrt{\frac{\mathrm{3}}{{y}^{\mathrm{2}} }+\mathrm{1}}\right)^{−\mathrm{2}} \right\}\:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{2}} {A}\left({y}\right){dy}\:...{be}\:{continued}... \\ $$
Commented by Tawa1 last updated on 29/Nov/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by maxmathsup by imad last updated on 01/Dec/18

$${thank}\:{you}\:{sir}\:. \\ $$
Answered by MJS last updated on 28/Nov/18
![(1) ∫(√(x^2 +y^2 ))dx= [t=arcsinh (x/y) → x=ysinh t ∧ dx=ycosh t dt] =∫ycosh t (√(y^2 +y^2 sinh^2 t))dt=y^2 ∫cosh^2 t dt= =(y^2 /2)∫cosh 2t dt+(y^2 /2)∫dt=(y^2 /4)sinh 2t +(y^2 /2)t= [y≥0] =(x/2)(√(x^2 +y^2 ))+(y^2 /2)arcsinh (x/y) ∫_(√(3y)) ^(√(4−y^2 )) (√(x^2 +y^2 ))dx=(√(4−y^2 ))+(y^2 /2)arcsinh ((√(4−y^2 ))/y) −(y/2)(√(3(y+3)))−(y^2 /2)arcsinh (√(3/y)) (2.1) ∫(√(4−y^2 ))dy= [u=arcsin (y/2) → y=2sin u ∧ dy=2cos u du] =∫2cos u (√(4−4sin^2 u))du=4∫cos^2 u du= =2∫cos 2u du+2∫du=sin 2u +2u= =(y/2)(√(4−y^2 ))+2arcsin (y/2) (2.2) ∫(y^2 /2)arcsinh ((√(4−y^2 ))/y) dy= [((∫f′g=fg−∫fg′ with: f′=(y^2 /2) → f=(y^3 /6))),((g=arcsinh ((√(4−y^2 ))/y) → g′=−(2/(y(√(4−y^2 )))))) ] =(y^3 /6)arcsinh ((√(4−y^2 ))/y) +(1/3)∫(y^2 /(√(4−y^2 )))dy= (1/3)∫(y^2 /(√(4−y^2 )))dy=(1/3)∫((y^2 −4+4)/(√(4−y^2 )))dy= =−(1/3)∫(√(4−y^2 ))dy+(4/3)∫(dy/(√(4−y^2 )))= =−(y/6)(√(4−y^2 ))+(2/3)arcsin (y/2) =(y^3 /6)arcsinh ((√(4−y^2 ))/y) −(y/6)(√(4−y^2 ))+(2/3)arcsin (y/2) (2.3) ∫−(y/2)(√(3(y+3)))dy=−((√3)/2)∫y(√(y+3))dy= [v=y+3 → dy=dv] =−((√3)/2)∫(v−3)(√v)dv=((3(√3))/2)∫v^(1/2) dv−((√3)/2)∫v^(3/2) dv= =(√3)v^(3/2) −((√3)/5)v^(5/2) =(√3)(y+3)^(3/2) −((√3)/5)(y+3)^(5/2) =((√3)/5)(2−y)(y+3)^(3/2) (2.4) ∫−(y^2 /2)arcsinh (√(3/y))dy=−(1/2)∫y^2 arcsinh (√(3/y))dy= [w=(y^3 /3) → dx=(dw/y^2 )] =−(1/2)∫arcsinh ((3)^(1/3) /(w)^(1/6) ) dw= [((∫f′g=fg−∫fg′ with: f′=1 → f=w)),((g=arcsinh ((3)^(1/3) /(w)^(1/6) ) → g′=−((3)^(1/3) /(6w(√((w)^(1/3) +(9)^(1/3) )))))) ] =−(w/2)arcsinh ((3)^(1/3) /(w)^(1/6) ) −((3)^(1/3) /(12))∫(dw/(√((w)^(1/3) +(9)^(1/3) ))) −((3)^(1/3) /(12))∫(dw/(√((w)^(1/3) +(9)^(1/3) )))= [z=(w)^(1/3) +(9)^(1/3) → dw=3(z−(9)^(1/3) )dz] =−((3)^(1/3) /4)∫z^(3/2) dz+(3/2)∫z^(1/2) dz−((3(9)^(1/3) )/4)∫z^(−(1/2)) dz= =−((3)^(1/3) /(10))z^(5/2) +z^(3/2) −((3(9)^(1/3) )/2)z^(1/2) =(−((3)^(1/3) /(10))(w^2 )^(1/3) +(2/5)(w)^(1/3) −((4(9)^(1/3) )/5))(√((w)^(1/3) +(9)^(1/3) )) =−(w/2)arcsinh ((3)^(1/3) /(w)^(1/6) ) −(((3)^(1/3) /(10))(w^2 )^(1/3) −(2/5)(w)^(1/3) +((4(9)^(1/3) )/5))(√((w)^(1/3) +(9)^(1/3) ))= =−(y^3 /6)arcsinh ((9)^(1/3) /y) −(1/(30))(y^2 −4y+24)(√(3(y+3))) ∫_0 ^2 (∫_(√(3y)) ^(√(4−y^2 )) (√(x^2 +y^2 ))dx)dy=((4π)/3)−(4/3)arcsinh ((9)^(1/3) /2) −((2(√(15)))/3)−(6/5)≈−.805740](Q48731.png)
$$\left(\mathrm{1}\right)\:\:\int\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{arcsinh}\:\frac{{x}}{{y}}\:\rightarrow\:{x}={y}\mathrm{sinh}\:{t}\:\wedge\:{dx}={y}\mathrm{cosh}\:{t}\:{dt}\right] \\ $$$$=\int{y}\mathrm{cosh}\:{t}\:\sqrt{{y}^{\mathrm{2}} +{y}^{\mathrm{2}} \mathrm{sinh}^{\mathrm{2}} \:{t}}{dt}={y}^{\mathrm{2}} \int\mathrm{cosh}^{\mathrm{2}} \:{t}\:{dt}= \\ $$$$=\frac{{y}^{\mathrm{2}} }{\mathrm{2}}\int\mathrm{cosh}\:\mathrm{2}{t}\:{dt}+\frac{{y}^{\mathrm{2}} }{\mathrm{2}}\int{dt}=\frac{{y}^{\mathrm{2}} }{\mathrm{4}}\mathrm{sinh}\:\mathrm{2}{t}\:+\frac{{y}^{\mathrm{2}} }{\mathrm{2}}{t}= \\ $$$$\:\:\:\:\:\left[{y}\geqslant\mathrm{0}\right] \\ $$$$=\frac{{x}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{\mathrm{2}}\mathrm{arcsinh}\:\frac{{x}}{{y}} \\ $$$$\underset{\sqrt{\mathrm{3}{y}}} {\overset{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }} {\int}}\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{dx}=\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{\mathrm{2}}\mathrm{arcsinh}\:\frac{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }}{{y}}\:−\frac{{y}}{\mathrm{2}}\sqrt{\mathrm{3}\left({y}+\mathrm{3}\right)}−\frac{{y}^{\mathrm{2}} }{\mathrm{2}}\mathrm{arcsinh}\:\sqrt{\frac{\mathrm{3}}{{y}}} \\ $$$$\left(\mathrm{2}.\mathrm{1}\right)\:\:\int\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }{dy}= \\ $$$$\:\:\:\:\:\left[{u}=\mathrm{arcsin}\:\frac{{y}}{\mathrm{2}}\:\rightarrow\:{y}=\mathrm{2sin}\:{u}\:\wedge\:{dy}=\mathrm{2cos}\:{u}\:{du}\right] \\ $$$$=\int\mathrm{2cos}\:{u}\:\sqrt{\mathrm{4}−\mathrm{4sin}^{\mathrm{2}} \:{u}}{du}=\mathrm{4}\int\mathrm{cos}^{\mathrm{2}} \:{u}\:{du}= \\ $$$$=\mathrm{2}\int\mathrm{cos}\:\mathrm{2}{u}\:{du}+\mathrm{2}\int{du}=\mathrm{sin}\:\mathrm{2}{u}\:+\mathrm{2}{u}= \\ $$$$=\frac{{y}}{\mathrm{2}}\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }+\mathrm{2arcsin}\:\frac{{y}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}.\mathrm{2}\right)\:\:\int\frac{{y}^{\mathrm{2}} }{\mathrm{2}}\mathrm{arcsinh}\:\frac{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }}{{y}}\:{dy}= \\ $$$$\:\:\:\:\:\begin{bmatrix}{\int{f}'{g}={fg}−\int{fg}'\:\mathrm{with}:\:{f}'=\frac{{y}^{\mathrm{2}} }{\mathrm{2}}\:\rightarrow\:{f}=\frac{{y}^{\mathrm{3}} }{\mathrm{6}}}\\{{g}=\mathrm{arcsinh}\:\frac{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }}{{y}}\:\rightarrow\:{g}'=−\frac{\mathrm{2}}{{y}\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }}}\end{bmatrix} \\ $$$$=\frac{{y}^{\mathrm{3}} }{\mathrm{6}}\mathrm{arcsinh}\:\frac{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }}{{y}}\:+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{y}^{\mathrm{2}} }{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }}{dy}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{y}^{\mathrm{2}} }{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }}{dy}=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{y}^{\mathrm{2}} −\mathrm{4}+\mathrm{4}}{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }}{dy}= \\ $$$$\:\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{3}}\int\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }{dy}+\frac{\mathrm{4}}{\mathrm{3}}\int\frac{{dy}}{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }}= \\ $$$$\:\:\:\:\:\:\:\:\:\:=−\frac{{y}}{\mathrm{6}}\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arcsin}\:\frac{{y}}{\mathrm{2}} \\ $$$$=\frac{{y}^{\mathrm{3}} }{\mathrm{6}}\mathrm{arcsinh}\:\frac{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }}{{y}}\:−\frac{{y}}{\mathrm{6}}\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arcsin}\:\frac{{y}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}.\mathrm{3}\right)\:\:\int−\frac{{y}}{\mathrm{2}}\sqrt{\mathrm{3}\left({y}+\mathrm{3}\right)}{dy}=−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\int{y}\sqrt{{y}+\mathrm{3}}{dy}= \\ $$$$\:\:\:\:\:\left[{v}={y}+\mathrm{3}\:\rightarrow\:{dy}={dv}\right] \\ $$$$=−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\int\left({v}−\mathrm{3}\right)\sqrt{{v}}{dv}=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\int{v}^{\frac{\mathrm{1}}{\mathrm{2}}} {dv}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\int{v}^{\frac{\mathrm{3}}{\mathrm{2}}} {dv}= \\ $$$$=\sqrt{\mathrm{3}}{v}^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\sqrt{\mathrm{3}}}{\mathrm{5}}{v}^{\frac{\mathrm{5}}{\mathrm{2}}} =\sqrt{\mathrm{3}}\left({y}+\mathrm{3}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\sqrt{\mathrm{3}}}{\mathrm{5}}\left({y}+\mathrm{3}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{5}}\left(\mathrm{2}−{y}\right)\left({y}+\mathrm{3}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\left(\mathrm{2}.\mathrm{4}\right)\:\:\int−\frac{{y}^{\mathrm{2}} }{\mathrm{2}}\mathrm{arcsinh}\:\sqrt{\frac{\mathrm{3}}{{y}}}{dy}=−\frac{\mathrm{1}}{\mathrm{2}}\int{y}^{\mathrm{2}} \mathrm{arcsinh}\:\sqrt{\frac{\mathrm{3}}{{y}}}{dy}= \\ $$$$\:\:\:\:\:\left[{w}=\frac{{y}^{\mathrm{3}} }{\mathrm{3}}\:\rightarrow\:{dx}=\frac{{dw}}{{y}^{\mathrm{2}} }\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{arcsinh}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}}}{\sqrt[{\mathrm{6}}]{{w}}}\:{dw}= \\ $$$$\:\:\:\:\:\begin{bmatrix}{\int{f}'{g}={fg}−\int{fg}'\:\mathrm{with}:\:{f}'=\mathrm{1}\:\rightarrow\:{f}={w}}\\{{g}=\mathrm{arcsinh}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}}}{\sqrt[{\mathrm{6}}]{{w}}}\:\rightarrow\:{g}'=−\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}}}{\mathrm{6}{w}\sqrt{\sqrt[{\mathrm{3}}]{{w}}+\sqrt[{\mathrm{3}}]{\mathrm{9}}}}}\end{bmatrix} \\ $$$$=−\frac{{w}}{\mathrm{2}}\mathrm{arcsinh}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}}}{\sqrt[{\mathrm{6}}]{{w}}}\:−\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}}}{\mathrm{12}}\int\frac{{dw}}{\sqrt{\sqrt[{\mathrm{3}}]{{w}}+\sqrt[{\mathrm{3}}]{\mathrm{9}}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:−\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}}}{\mathrm{12}}\int\frac{{dw}}{\sqrt{\sqrt[{\mathrm{3}}]{{w}}+\sqrt[{\mathrm{3}}]{\mathrm{9}}}}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{z}=\sqrt[{\mathrm{3}}]{{w}}+\sqrt[{\mathrm{3}}]{\mathrm{9}}\:\rightarrow\:{dw}=\mathrm{3}\left({z}−\sqrt[{\mathrm{3}}]{\mathrm{9}}\right){dz}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:=−\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}}}{\mathrm{4}}\int{z}^{\frac{\mathrm{3}}{\mathrm{2}}} {dz}+\frac{\mathrm{3}}{\mathrm{2}}\int{z}^{\frac{\mathrm{1}}{\mathrm{2}}} {dz}−\frac{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{9}}}{\mathrm{4}}\int{z}^{−\frac{\mathrm{1}}{\mathrm{2}}} {dz}= \\ $$$$\:\:\:\:\:\:\:\:\:\:=−\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}}}{\mathrm{10}}{z}^{\frac{\mathrm{5}}{\mathrm{2}}} +{z}^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{9}}}{\mathrm{2}}{z}^{\frac{\mathrm{1}}{\mathrm{2}}} =\left(−\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}}}{\mathrm{10}}\sqrt[{\mathrm{3}}]{{w}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{5}}\sqrt[{\mathrm{3}}]{{w}}−\frac{\mathrm{4}\sqrt[{\mathrm{3}}]{\mathrm{9}}}{\mathrm{5}}\right)\sqrt{\sqrt[{\mathrm{3}}]{{w}}+\sqrt[{\mathrm{3}}]{\mathrm{9}}} \\ $$$$=−\frac{{w}}{\mathrm{2}}\mathrm{arcsinh}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}}}{\sqrt[{\mathrm{6}}]{{w}}}\:−\left(\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}}}{\mathrm{10}}\sqrt[{\mathrm{3}}]{{w}^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{5}}\sqrt[{\mathrm{3}}]{{w}}+\frac{\mathrm{4}\sqrt[{\mathrm{3}}]{\mathrm{9}}}{\mathrm{5}}\right)\sqrt{\sqrt[{\mathrm{3}}]{{w}}+\sqrt[{\mathrm{3}}]{\mathrm{9}}}= \\ $$$$=−\frac{{y}^{\mathrm{3}} }{\mathrm{6}}\mathrm{arcsinh}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{9}}}{{y}}\:−\frac{\mathrm{1}}{\mathrm{30}}\left({y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{24}\right)\sqrt{\mathrm{3}\left({y}+\mathrm{3}\right)} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\left(\underset{\sqrt{\mathrm{3}{y}}} {\overset{\sqrt{\mathrm{4}−{y}^{\mathrm{2}} }} {\int}}\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{dx}\right){dy}=\frac{\mathrm{4}\pi}{\mathrm{3}}−\frac{\mathrm{4}}{\mathrm{3}}\mathrm{arcsinh}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{9}}}{\mathrm{2}}\:−\frac{\mathrm{2}\sqrt{\mathrm{15}}}{\mathrm{3}}−\frac{\mathrm{6}}{\mathrm{5}}\approx−.\mathrm{805740} \\ $$
Commented by MJS last updated on 28/Nov/18

$$...\mathrm{please}\:\mathrm{someone}\:\mathrm{check}\:\mathrm{for}\:\mathrm{typos}.\:\mathrm{it}'\mathrm{s}\:\mathrm{3}\:\mathrm{a}.\mathrm{m}. \\ $$$$\mathrm{and}\:\mathrm{I}'\mathrm{m}\:\mathrm{really}\:\mathrm{tired}... \\ $$
Commented by maxmathsup by imad last updated on 28/Nov/18
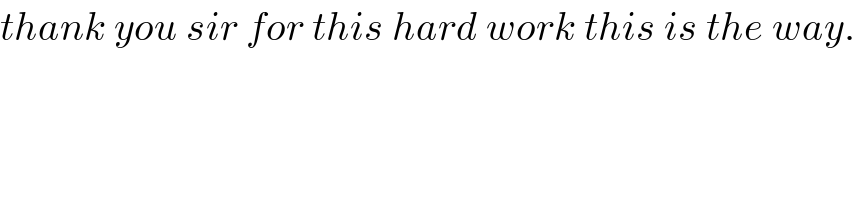
$${thank}\:{you}\:{sir}\:{for}\:{this}\:{hard}\:{work}\:{this}\:{is}\:{the}\:{way}. \\ $$
Commented by MJS last updated on 28/Nov/18

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$
Commented by Tawa1 last updated on 29/Nov/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
