Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 188753 by BaliramKumar last updated on 19/Mar/23

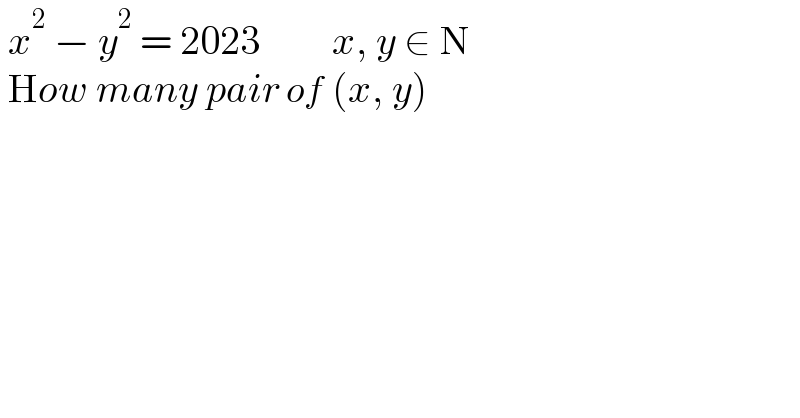
x^2 − y^2 = 2023 x, y ∈ N How many pair of (x, y)

$$\:{x}^{\mathrm{2}} \:−\:{y}^{\mathrm{2}} \:=\:\mathrm{2023}\:\:\:\:\:\:\:\:\:{x},\:{y}\:\in\:\mathrm{N} \\ $$$$\:\mathrm{H}{ow}\:{many}\:{pair}\:{of}\:\left({x},\:{y}\right) \\ $$

Answered by BaliramKumar last updated on 19/Mar/23

solution:− x^2 −y^2 =2023 d = 2023 d = 2023 = 7^1 ×17^2 total factor of 2023 = (1+1)(2+1) = 6 No. of pairs (x, y) = ⌊(6/2)⌋ = 3 {: ((2023 = 1×2023)),((2023 = 7×289)),((2023 = 17×119)) } 3 pair { (((1012, 1011))),(((148, 141))),(((68, 51))) :} x = ((2023+1)/2) = 1012, y = ((2023−1)/2) = 1011 x = ((289+7)/2) = 148, y = ((289−7)/2) = 141 x = ((119+17)/2) = 68, y = ((119−17)/2) = 51 Pair =⌊∣((No. of even factor−No. of odd factor)/2)∣⌋

$${solution}:− \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{2023}\: \\ $$$${d}\:=\:\mathrm{2023}\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$${d}\:=\:\mathrm{2023}\:=\:\mathrm{7}^{\mathrm{1}} ×\mathrm{17}^{\mathrm{2}} \\ $$$${total}\:{factor}\:{of}\:\mathrm{2023}\:=\:\left(\mathrm{1}+\mathrm{1}\right)\left(\mathrm{2}+\mathrm{1}\right)\:=\:\mathrm{6} \\ $$$${No}.\:{of}\:{pairs}\:\left({x},\:{y}\right)\:=\:\lfloor\frac{\mathrm{6}}{\mathrm{2}}\rfloor\:=\:\mathrm{3}\:\:\:\:\:\:\:\: \\ $$$$\left.\begin{matrix}{\mathrm{2023}\:=\:\mathrm{1}×\mathrm{2023}}\\{\mathrm{2023}\:=\:\mathrm{7}×\mathrm{289}}\\{\mathrm{2023}\:=\:\mathrm{17}×\mathrm{119}}\end{matrix}\right\}\:\mathrm{3}\:{pair}\:\begin{cases}{\left(\mathrm{1012},\:\mathrm{1011}\right)}\\{\left(\mathrm{148},\:\mathrm{141}\right)}\\{\left(\mathrm{68},\:\mathrm{51}\right)}\end{cases} \\ $$$${x}\:=\:\frac{\mathrm{2023}+\mathrm{1}}{\mathrm{2}}\:=\:\mathrm{1012},\:\:\:\:\:\:{y}\:=\:\frac{\mathrm{2023}−\mathrm{1}}{\mathrm{2}}\:=\:\mathrm{1011} \\ $$$${x}\:=\:\frac{\mathrm{289}+\mathrm{7}}{\mathrm{2}}\:=\:\mathrm{148},\:\:\:\:\:\:{y}\:=\:\frac{\mathrm{289}−\mathrm{7}}{\mathrm{2}}\:=\:\mathrm{141} \\ $$$${x}\:=\:\frac{\mathrm{119}+\mathrm{17}}{\mathrm{2}}\:=\:\mathrm{68},\:\:\:\:\:\:{y}\:=\:\frac{\mathrm{119}−\mathrm{17}}{\mathrm{2}}\:=\:\mathrm{51} \\ $$$$ \\ $$$${Pair}\:=\lfloor\mid\frac{{No}.\:{of}\:{even}\:{factor}−{No}.\:{of}\:{odd}\:{factor}}{\mathrm{2}}\mid\rfloor \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com