Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 129777 by stelor last updated on 18/Jan/21

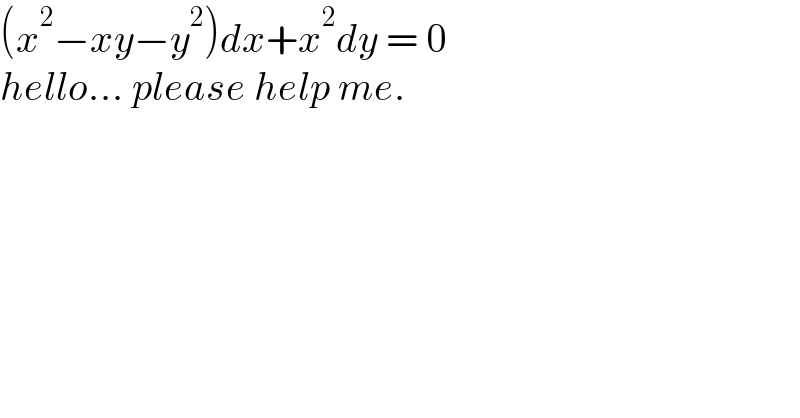
(x^2 −xy−y^2 )dx+x^2 dy = 0 hello... please help me.

$$\left({x}^{\mathrm{2}} −{xy}−{y}^{\mathrm{2}} \right){dx}+{x}^{\mathrm{2}} {dy}\:=\:\mathrm{0} \\ $$$${hello}...\:{please}\:{help}\:{me}. \\ $$

Answered by Ar Brandon last updated on 18/Jan/21

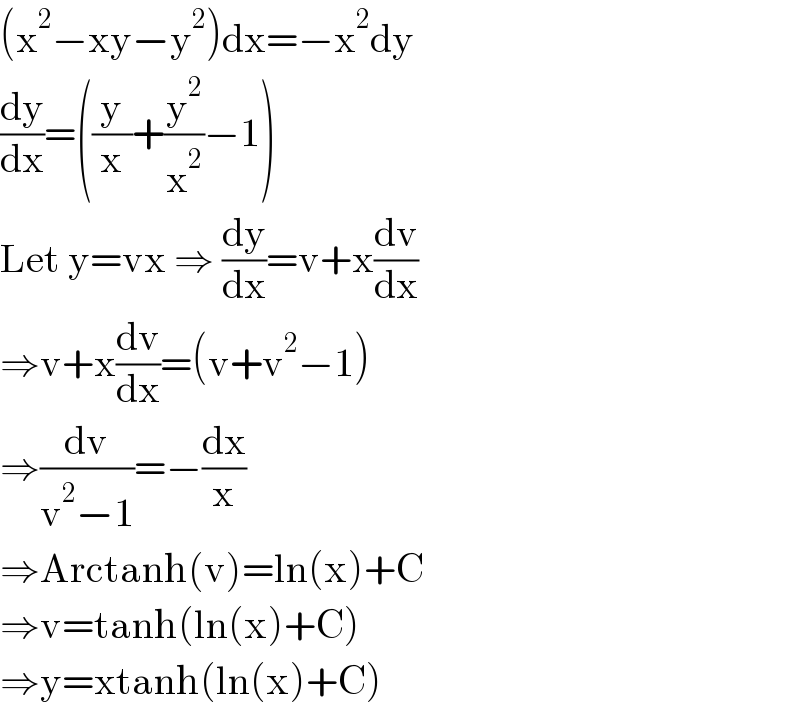
(x^2 −xy−y^2 )dx=−x^2 dy (dy/dx)=((y/x)+(y^2 /x^2 )−1) Let y=vx ⇒ (dy/dx)=v+x(dv/dx) ⇒v+x(dv/dx)=(v+v^2 −1) ⇒(dv/(v^2 −1))=−(dx/x) ⇒Arctanh(v)=ln(x)+C ⇒v=tanh(ln(x)+C) ⇒y=xtanh(ln(x)+C)

$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{xy}−\mathrm{y}^{\mathrm{2}} \right)\mathrm{dx}=−\mathrm{x}^{\mathrm{2}} \mathrm{dy} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\left(\frac{\mathrm{y}}{\mathrm{x}}+\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }−\mathrm{1}\right) \\ $$$$\mathrm{Let}\:\mathrm{y}=\mathrm{vx}\:\Rightarrow\:\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{v}+\mathrm{x}\frac{\mathrm{dv}}{\mathrm{dx}} \\ $$$$\Rightarrow\mathrm{v}+\mathrm{x}\frac{\mathrm{dv}}{\mathrm{dx}}=\left(\mathrm{v}+\mathrm{v}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\Rightarrow\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{1}}=−\frac{\mathrm{dx}}{\mathrm{x}} \\ $$$$\Rightarrow\mathrm{Arctanh}\left(\mathrm{v}\right)=\mathrm{ln}\left(\mathrm{x}\right)+\mathrm{C} \\ $$$$\Rightarrow\mathrm{v}=\mathrm{tanh}\left(\mathrm{ln}\left(\mathrm{x}\right)+\mathrm{C}\right) \\ $$$$\Rightarrow\mathrm{y}=\mathrm{xtanh}\left(\mathrm{ln}\left(\mathrm{x}\right)+\mathrm{C}\right) \\ $$

Commented by stelor last updated on 18/Jan/21

thank... cool .

$${thank}...\:{cool}\:\:\:. \\ $$

Answered by bramlexs22 last updated on 19/Jan/21

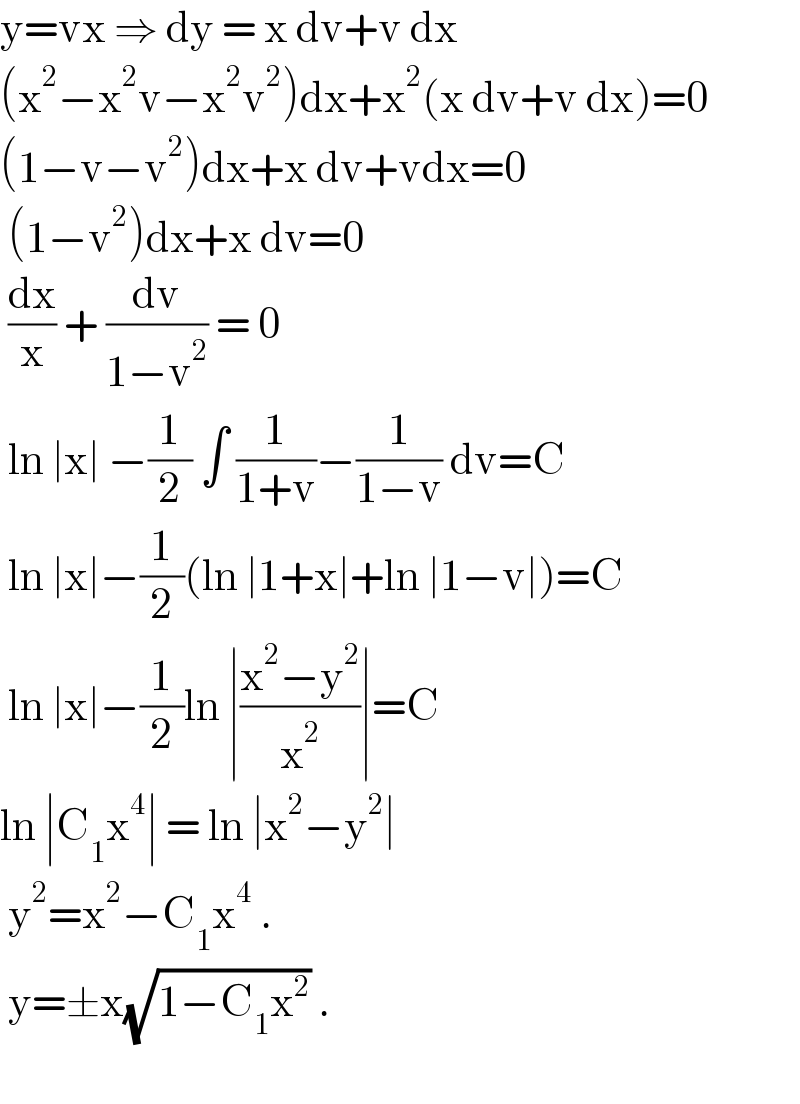
y=vx ⇒ dy = x dv+v dx (x^2 −x^2 v−x^2 v^2 )dx+x^2 (x dv+v dx)=0 (1−v−v^2 )dx+x dv+vdx=0 (1−v^2 )dx+x dv=0 (dx/x) + (dv/(1−v^2 )) = 0 ln ∣x∣ −(1/2) ∫ (1/(1+v))−(1/(1−v)) dv=C ln ∣x∣−(1/2)(ln ∣1+x∣+ln ∣1−v∣)=C ln ∣x∣−(1/2)ln ∣((x^2 −y^2 )/x^2 )∣=C ln ∣C_1 x^4 ∣ = ln ∣x^2 −y^2 ∣ y^2 =x^2 −C_1 x^4 . y=±x(√(1−C_1 x^2 )) .

$$\mathrm{y}=\mathrm{vx}\:\Rightarrow\:\mathrm{dy}\:=\:\mathrm{x}\:\mathrm{dv}+\mathrm{v}\:\mathrm{dx} \\ $$$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} \mathrm{v}−\mathrm{x}^{\mathrm{2}} \mathrm{v}^{\mathrm{2}} \right)\mathrm{dx}+\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}\:\mathrm{dv}+\mathrm{v}\:\mathrm{dx}\right)=\mathrm{0} \\ $$$$\left(\mathrm{1}−\mathrm{v}−\mathrm{v}^{\mathrm{2}} \right)\mathrm{dx}+\mathrm{x}\:\mathrm{dv}+\mathrm{vdx}=\mathrm{0} \\ $$$$\:\left(\mathrm{1}−\mathrm{v}^{\mathrm{2}} \right)\mathrm{dx}+\mathrm{x}\:\mathrm{dv}=\mathrm{0} \\ $$$$\:\frac{\mathrm{dx}}{\mathrm{x}}\:+\:\frac{\mathrm{dv}}{\mathrm{1}−\mathrm{v}^{\mathrm{2}} }\:=\:\mathrm{0} \\ $$$$\:\mathrm{ln}\:\mid\mathrm{x}\mid\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{v}}−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{v}}\:\mathrm{dv}=\mathrm{C} \\ $$$$\:\mathrm{ln}\:\mid\mathrm{x}\mid−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ln}\:\mid\mathrm{1}+\mathrm{x}\mid+\mathrm{ln}\:\mid\mathrm{1}−\mathrm{v}\mid\right)=\mathrm{C} \\ $$$$\:\mathrm{ln}\:\mid\mathrm{x}\mid−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\mid=\mathrm{C} \\ $$$$\mathrm{ln}\:\mid\mathrm{C}_{\mathrm{1}} \mathrm{x}^{\mathrm{4}} \mid\:=\:\mathrm{ln}\:\mid\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \mid\: \\ $$$$\:\mathrm{y}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} −\mathrm{C}_{\mathrm{1}} \mathrm{x}^{\mathrm{4}} \:. \\ $$$$\:\mathrm{y}=\pm\mathrm{x}\sqrt{\mathrm{1}−\mathrm{C}_{\mathrm{1}} \mathrm{x}^{\mathrm{2}} }\:. \\ $$$$\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com