
Question Number 209694 by Frix last updated on 18/Jul/24
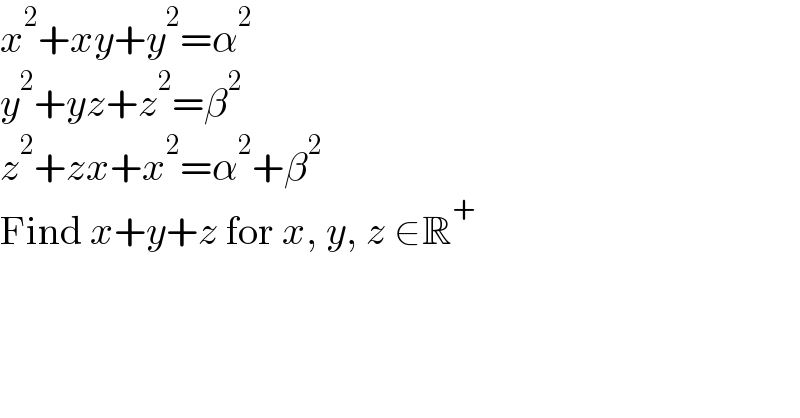
$${x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} =\alpha^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} +{yz}+{z}^{\mathrm{2}} =\beta^{\mathrm{2}} \\ $$$${z}^{\mathrm{2}} +{zx}+{x}^{\mathrm{2}} =\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \\ $$$$\mathrm{Find}\:{x}+{y}+{z}\:\mathrm{for}\:{x},\:{y},\:{z}\:\in\mathbb{R}^{+} \\ $$
Answered by mr W last updated on 18/Jul/24
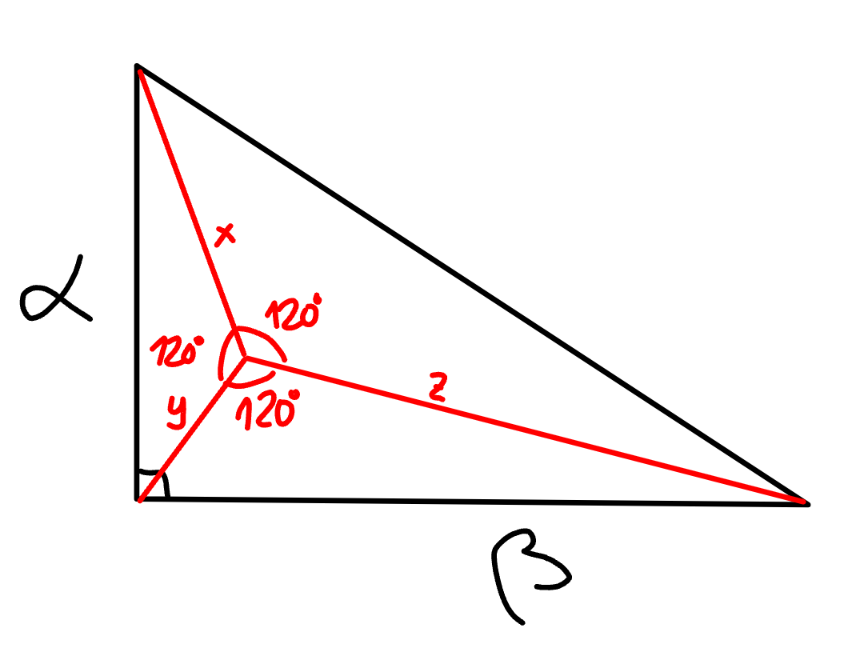
Commented by mr W last updated on 18/Jul/24
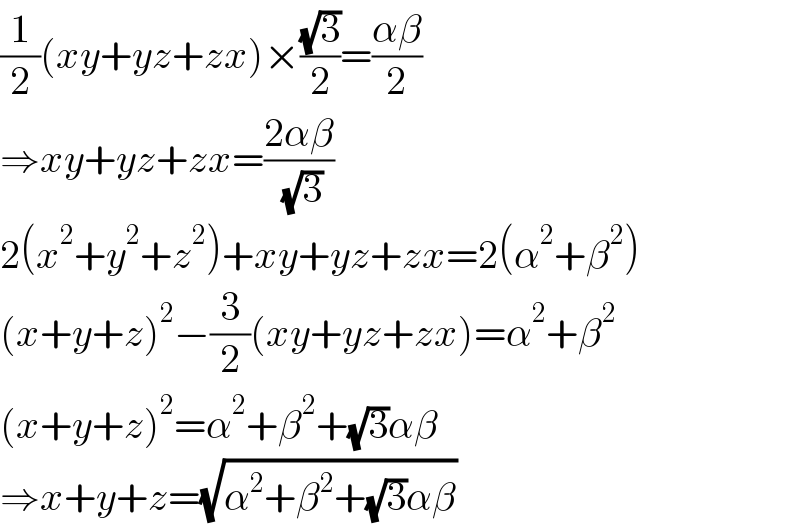
$$\frac{\mathrm{1}}{\mathrm{2}}\left({xy}+{yz}+{zx}\right)×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\alpha\beta}{\mathrm{2}} \\ $$$$\Rightarrow{xy}+{yz}+{zx}=\frac{\mathrm{2}\alpha\beta}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{2}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)+{xy}+{yz}+{zx}=\mathrm{2}\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right) \\ $$$$\left({x}+{y}+{z}\right)^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}\left({xy}+{yz}+{zx}\right)=\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \\ $$$$\left({x}+{y}+{z}\right)^{\mathrm{2}} =\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\sqrt{\mathrm{3}}\alpha\beta \\ $$$$\Rightarrow{x}+{y}+{z}=\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\sqrt{\mathrm{3}}\alpha\beta} \\ $$
Commented by Frix last updated on 18/Jul/24
��
