
Previous in Differential Equation Next in Differential Equation
Question Number 100684 by bemath last updated on 28/Jun/20
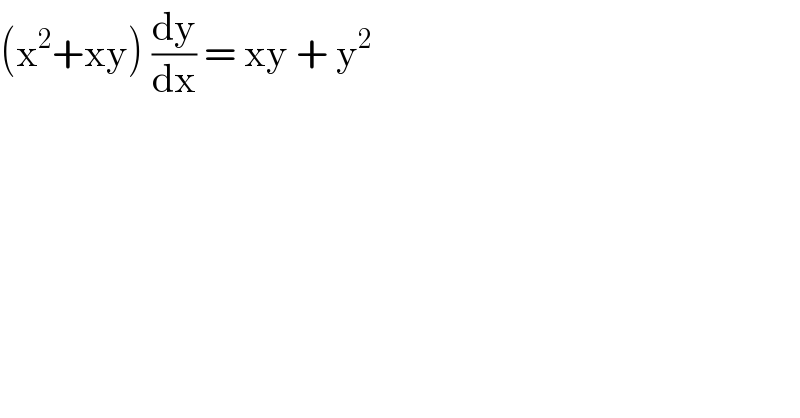
$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{xy}\right)\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{xy}\:+\:\mathrm{y}^{\mathrm{2}} \\ $$
Answered by bobhans last updated on 28/Jun/20
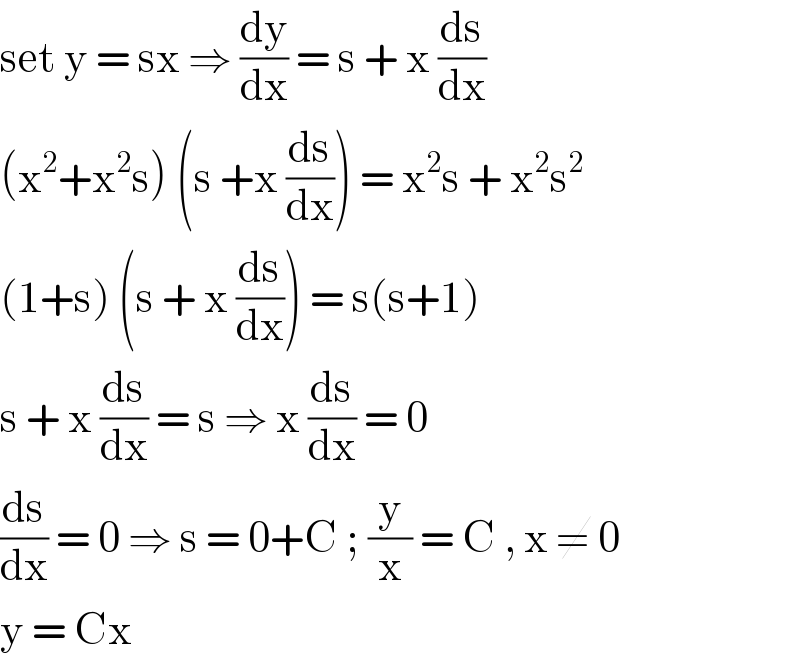
$$\mathrm{set}\:\mathrm{y}\:=\:\mathrm{sx}\:\Rightarrow\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{s}\:+\:\mathrm{x}\:\frac{\mathrm{ds}}{\mathrm{dx}} \\ $$$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \mathrm{s}\right)\:\left(\mathrm{s}\:+\mathrm{x}\:\frac{\mathrm{ds}}{\mathrm{dx}}\right)\:=\:\mathrm{x}^{\mathrm{2}} \mathrm{s}\:+\:\mathrm{x}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+\mathrm{s}\right)\:\left(\mathrm{s}\:+\:\mathrm{x}\:\frac{\mathrm{ds}}{\mathrm{dx}}\right)\:=\:\mathrm{s}\left(\mathrm{s}+\mathrm{1}\right) \\ $$$$\mathrm{s}\:+\:\mathrm{x}\:\frac{\mathrm{ds}}{\mathrm{dx}}\:=\:\mathrm{s}\:\Rightarrow\:\mathrm{x}\:\frac{\mathrm{ds}}{\mathrm{dx}}\:=\:\mathrm{0}\: \\ $$$$\frac{\mathrm{ds}}{\mathrm{dx}}\:=\:\mathrm{0}\:\Rightarrow\:\mathrm{s}\:=\:\mathrm{0}+\mathrm{C}\:;\:\frac{\mathrm{y}}{\mathrm{x}}\:=\:\mathrm{C}\:,\:\mathrm{x}\:\neq\:\mathrm{0}\: \\ $$$$\mathrm{y}\:=\:\mathrm{Cx}\: \\ $$
