Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 43391 by gunawan last updated on 10/Sep/18

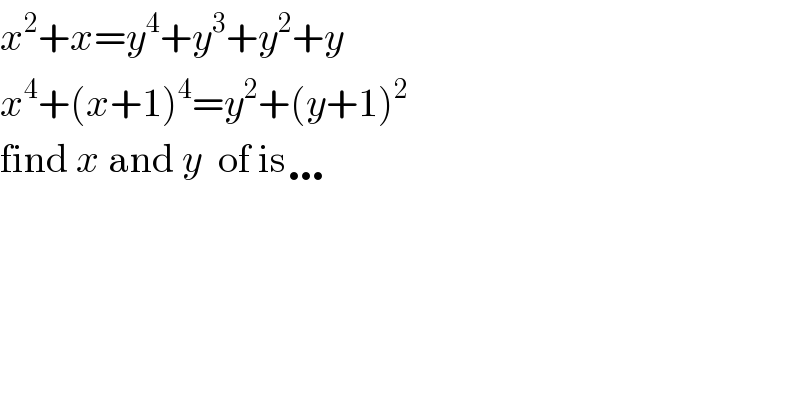
x^2 +x=y^4 +y^3 +y^2 +y x^4 +(x+1)^4 =y^2 +(y+1)^2 find x and y of is…

$${x}^{\mathrm{2}} +{x}={y}^{\mathrm{4}} +{y}^{\mathrm{3}} +{y}^{\mathrm{2}} +{y} \\ $$$${x}^{\mathrm{4}} +\left({x}+\mathrm{1}\right)^{\mathrm{4}} ={y}^{\mathrm{2}} +\left({y}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{find}\:{x}\:\mathrm{and}\:{y}\:\:\mathrm{of}\:\mathrm{is}\ldots \\ $$$$ \\ $$

Answered by ajfour last updated on 10/Sep/18

eq.(2) ⇒ 2x^4 +4x^3 +6x^2 +4x=2y^2 +2y ⇒ x^4 +2x^3 +3x^2 +2x=y(y+1) ⇒ x(x+1)(x^2 +1)+x(x+1)^2 =y(y+1) ....(i) eq.(1) ⇒ x(x+1)=y(y+1)(y^2 +1) ....(ii) if (x,y) ≠ (0,0), (−1,0), (0,−1) and (−1,−1) then (ii) ÷(i): x^2 +1 +x+1 = (1/(y^2 +1)) ⇒ x(x+1)+2 = (1/(y^2 +1)) substituting in (ii): (1/(y^2 +1))−2 = y(y+1)(y^2 +1) ⇒ [y(y+1)+2](y^2 +1)^2 = 1 ⇒ (y^2 +y+2)(y^4 +2y^2 +1)=1 ⇒ y^6 +y^5 +4y^4 +2y^3 +5y^2 +y+1=0 No real solutions to the above eq. Hence (x,y) ∈ [ (0,0), (0,−1), (−1,0), (−1,−1) ] .

$${eq}.\left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\mathrm{2}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{4}{x}=\mathrm{2}{y}^{\mathrm{2}} +\mathrm{2}{y} \\ $$$$\Rightarrow\:{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}={y}\left({y}+\mathrm{1}\right) \\ $$$$\Rightarrow\:\:{x}\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)+{x}\left({x}+\mathrm{1}\right)^{\mathrm{2}} ={y}\left({y}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:....\left({i}\right) \\ $$$${eq}.\left(\mathrm{1}\right)\:\Rightarrow \\ $$$${x}\left({x}+\mathrm{1}\right)={y}\left({y}+\mathrm{1}\right)\left({y}^{\mathrm{2}} +\mathrm{1}\right)\:\:\:\:....\left({ii}\right) \\ $$$${if}\:\:\left({x},{y}\right)\:\neq\:\left(\mathrm{0},\mathrm{0}\right),\:\left(−\mathrm{1},\mathrm{0}\right),\:\left(\mathrm{0},−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{and}\:\:\left(−\mathrm{1},−\mathrm{1}\right)\:\:{then} \\ $$$$\:\left({ii}\right)\:\boldsymbol{\div}\left({i}\right):\:\:\:\: \\ $$$${x}^{\mathrm{2}} +\mathrm{1}\:+{x}+\mathrm{1}\:=\:\frac{\mathrm{1}}{{y}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow\:\:{x}\left({x}+\mathrm{1}\right)+\mathrm{2}\:=\:\frac{\mathrm{1}}{{y}^{\mathrm{2}} +\mathrm{1}} \\ $$$${substituting}\:{in}\:\left({ii}\right): \\ $$$$\frac{\mathrm{1}}{{y}^{\mathrm{2}} +\mathrm{1}}−\mathrm{2}\:=\:{y}\left({y}+\mathrm{1}\right)\left({y}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\Rightarrow\:\:\left[{y}\left({y}+\mathrm{1}\right)+\mathrm{2}\right]\left({y}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} =\:\mathrm{1} \\ $$$$\Rightarrow\:\:\left({y}^{\mathrm{2}} +{y}+\mathrm{2}\right)\left({y}^{\mathrm{4}} +\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{1} \\ $$$$\Rightarrow\:\:{y}^{\mathrm{6}} +{y}^{\mathrm{5}} +\mathrm{4}{y}^{\mathrm{4}} +\mathrm{2}{y}^{\mathrm{3}} +\mathrm{5}{y}^{\mathrm{2}} +{y}+\mathrm{1}=\mathrm{0} \\ $$$${No}\:{real}\:{solutions}\:{to}\:{the}\:{above}\:{eq}. \\ $$$${Hence}\:\:\:\left({x},{y}\right)\:\in\:\left[\:\left(\mathrm{0},\mathrm{0}\right),\:\left(\mathrm{0},−\mathrm{1}\right),\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(−\mathrm{1},\mathrm{0}\right),\:\left(−\mathrm{1},−\mathrm{1}\right)\:\right]\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com