
Question Number 138673 by KwesiDerek last updated on 16/Apr/21

$$\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\boldsymbol{\mathrm{x}}=\mathrm{72} \\ $$$$\boldsymbol{\mathrm{y}}^{\mathrm{2}} −\boldsymbol{\mathrm{y}}=\mathrm{30} \\ $$$$\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}=\mathrm{4} \\ $$$$\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{y}}=? \\ $$
Commented by Rasheed.Sindhi last updated on 16/Apr/21
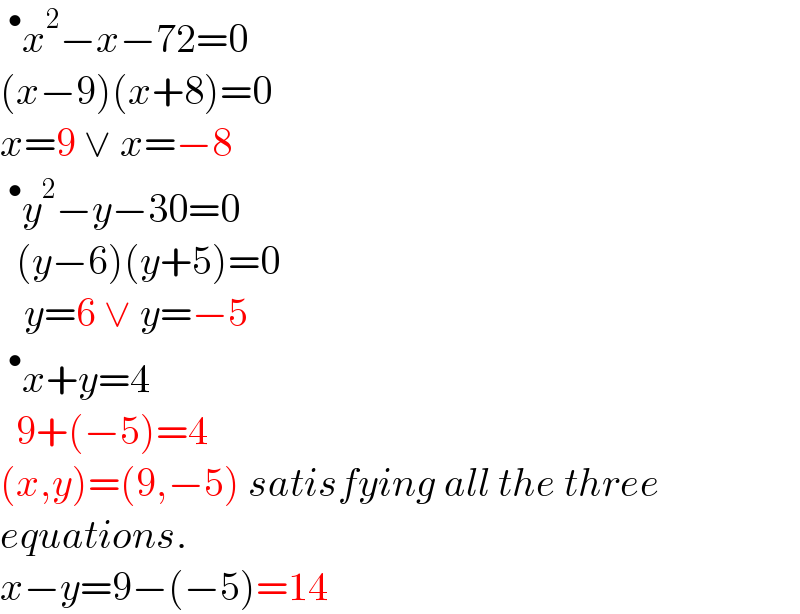
$$\:^{\bullet} {x}^{\mathrm{2}} −{x}−\mathrm{72}=\mathrm{0} \\ $$$$\left({x}−\mathrm{9}\right)\left({x}+\mathrm{8}\right)=\mathrm{0} \\ $$$${x}=\mathrm{9}\:\vee\:{x}=−\mathrm{8} \\ $$$$\:^{\bullet} {y}^{\mathrm{2}} −{y}−\mathrm{30}=\mathrm{0} \\ $$$$\:\:\left({y}−\mathrm{6}\right)\left({y}+\mathrm{5}\right)=\mathrm{0} \\ $$$$\:\:\:{y}=\mathrm{6}\:\vee\:{y}=−\mathrm{5} \\ $$$$\:^{\bullet} {x}+{y}=\mathrm{4} \\ $$$$\:\:\mathrm{9}+\left(−\mathrm{5}\right)=\mathrm{4} \\ $$$$\left({x},{y}\right)=\left(\mathrm{9},−\mathrm{5}\right)\:{satisfying}\:{all}\:{the}\:{three} \\ $$$${equations}. \\ $$$${x}−{y}=\mathrm{9}−\left(−\mathrm{5}\right)=\mathrm{14} \\ $$
Commented by Rasheed.Sindhi last updated on 16/Apr/21

$$\mathcal{S}{o}\:{I}\:{think}\:{nimnim}\:{is}\:{right}\:{here}. \\ $$
Commented by MJS_new last updated on 17/Apr/21
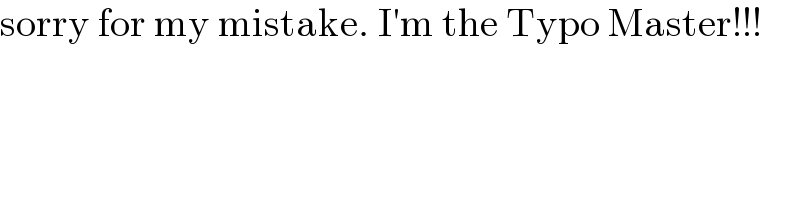
$$\mathrm{sorry}\:\mathrm{for}\:\mathrm{my}\:\mathrm{mistake}.\:\mathrm{I}'\mathrm{m}\:\mathrm{the}\:\mathrm{Typo}\:\mathrm{Master}!!! \\ $$
Answered by MJS_new last updated on 16/Apr/21

$${x}=−\mathrm{9}\vee{x}=\mathrm{8} \\ $$$${y}=−\mathrm{5}\vee{y}=\mathrm{6} \\ $$$$\Rightarrow\:{x}+{y}\neq\mathrm{4} \\ $$
Commented by Rasheed.Sindhi last updated on 17/Apr/21
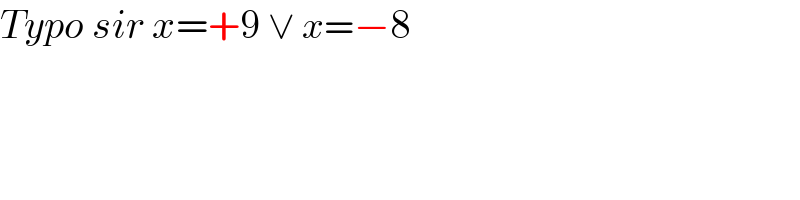
$${Typo}\:{sir}\:{x}=+\mathrm{9}\:\vee\:{x}=−\mathrm{8} \\ $$
Answered by nimnim last updated on 16/Apr/21

$${x}^{\mathrm{2}} −{x}=\mathrm{72}......\left({i}\right) \\ $$$${y}^{\mathrm{2}} −{y}=\mathrm{30}.......\left({ii}\right) \\ $$$${x}+{y}=\mathrm{4}..........\left({iii}\right) \\ $$$$\left({i}\right)+\left({ii}\right)\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{x}−{y}=\mathrm{102} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{xy}−\left({x}+{y}\right)=\mathrm{102} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\left(\mathrm{4}\right)^{\mathrm{2}} −\mathrm{2}{xy}−\mathrm{4}=\mathrm{102}\:\:\:\:\left\{{using}\:\left({iii}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{xy}=−\mathrm{45} \\ $$$$\left({iii}\right)\rightarrow\left({x}+{y}\right)^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} \\ $$$$\:\:\:\Rightarrow\left({x}−{y}\right)^{\mathrm{2}} +\mathrm{4}{xy}=\mathrm{16} \\ $$$$\:\:\:\Rightarrow\left({x}−{y}\right)^{\mathrm{2}} +\mathrm{4}\left(−\mathrm{45}\right)=\mathrm{16} \\ $$$$\:\:\:\Rightarrow\left({x}−{y}\right)^{\mathrm{2}} =\mathrm{16}+\mathrm{180} \\ $$$$\:\:\:\Rightarrow\left({x}−{y}\right)=\pm\sqrt{\mathrm{196}}=\pm\mathrm{14} \\ $$$$\:\:\:\Rightarrow\left({x}−{y}\right)=\mathrm{14}\:{or}\:\left({x}−{y}\right)=−\mathrm{14}\:\left({neglected}\right) \\ $$$$\therefore\:\left({x}−{y}\right)=\mathrm{14}\bigstar \\ $$
Commented by MJS_new last updated on 16/Apr/21
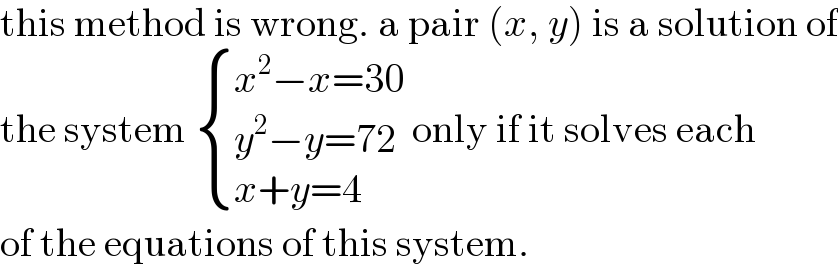
$$\mathrm{this}\:\mathrm{method}\:\mathrm{is}\:\mathrm{wrong}.\:\mathrm{a}\:\mathrm{pair}\:\left({x},\:{y}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{system}\:\begin{cases}{{x}^{\mathrm{2}} −{x}=\mathrm{30}}\\{{y}^{\mathrm{2}} −{y}=\mathrm{72}}\\{{x}+{y}=\mathrm{4}}\end{cases}\:\mathrm{only}\:\mathrm{if}\:\mathrm{it}\:\mathrm{solves}\:\mathrm{each} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{equations}\:\mathrm{of}\:\mathrm{this}\:\mathrm{system}. \\ $$
Commented by nimnim last updated on 16/Apr/21

$${I}\:{think}\:{x}=\mathrm{9}\:{and}\:{y}=−\mathrm{5} \\ $$
Commented by MJS_new last updated on 16/Apr/21
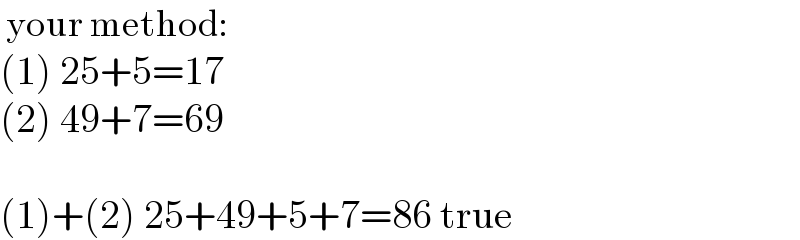
$$\:\mathrm{your}\:\mathrm{method}: \\ $$$$\left(\mathrm{1}\right)\:\mathrm{25}+\mathrm{5}=\mathrm{17} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{49}+\mathrm{7}=\mathrm{69} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\:\mathrm{25}+\mathrm{49}+\mathrm{5}+\mathrm{7}=\mathrm{86}\:\mathrm{true} \\ $$
Commented by MJS_new last updated on 16/Apr/21

$$\mathrm{if}\:{x}=\mathrm{9}\:\mathrm{the}\:\mathrm{first}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{wrong} \\ $$$$\mathrm{if}\:{y}=−\mathrm{5}\:\mathrm{the}\:\mathrm{second}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{wrong} \\ $$
Commented by nimnim last updated on 16/Apr/21

$${If}\:{x}=\mathrm{9},\:\mathrm{1}{st}\:{equation}=\mathrm{9}^{\mathrm{2}} −\mathrm{9}=\mathrm{81}−\mathrm{9}=\mathrm{72}\:{true} \\ $$$${If}\:{y}=−\mathrm{5},\:\mathrm{2}{nd}\:{equation}=\left(−\mathrm{5}\right)^{\mathrm{2}} −\left(−\mathrm{5}\right)=\mathrm{25}+\mathrm{5}=\mathrm{30}\:{true} \\ $$$$\mathrm{3}{rd}\:{equation}=\mathrm{9}+\left(−\mathrm{5}\right)=\mathrm{4}\:{true} \\ $$$$ \\ $$$${But}\:{if}\:{you}\:{say}\:{so},\:{it}\:{might}\:{be}\:{wrong}.\:{I}\:{am}\: \\ $$$${just}\:{a}\:{beginner},\:{reading}\:{in}\:\mathrm{8}\:{standard}.\:{I}\:{dont} \\ $$$${know}\:{much}\:{about}\:{maths}\:{like}\:{you}\:{do}. \\ $$$${Thanks}\:{for}\:{your}\:{help},\:{Sir}. \\ $$$$\:\: \\ $$
Answered by ajfour last updated on 16/Apr/21
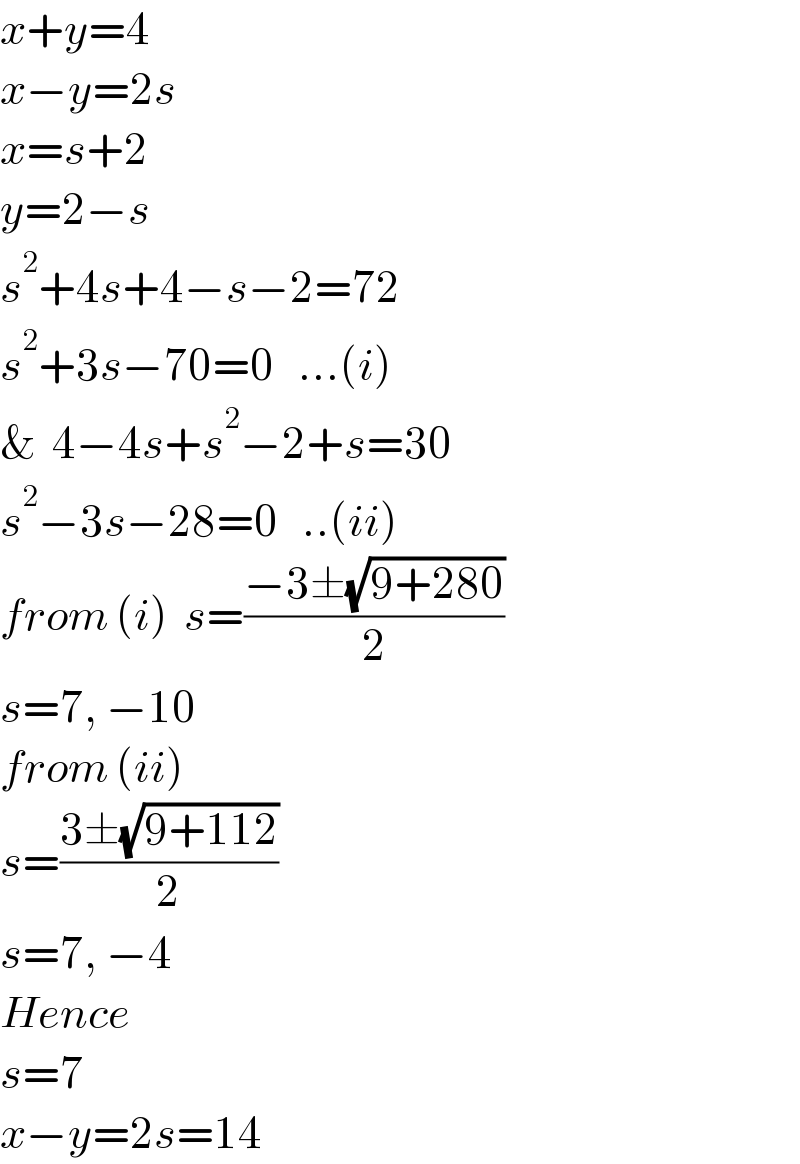
$${x}+{y}=\mathrm{4} \\ $$$${x}−{y}=\mathrm{2}{s} \\ $$$${x}={s}+\mathrm{2} \\ $$$${y}=\mathrm{2}−{s} \\ $$$${s}^{\mathrm{2}} +\mathrm{4}{s}+\mathrm{4}−{s}−\mathrm{2}=\mathrm{72} \\ $$$${s}^{\mathrm{2}} +\mathrm{3}{s}−\mathrm{70}=\mathrm{0}\:\:\:...\left({i}\right) \\ $$$$\&\:\:\mathrm{4}−\mathrm{4}{s}+{s}^{\mathrm{2}} −\mathrm{2}+{s}=\mathrm{30} \\ $$$${s}^{\mathrm{2}} −\mathrm{3}{s}−\mathrm{28}=\mathrm{0}\:\:\:..\left({ii}\right) \\ $$$${from}\:\left({i}\right)\:\:{s}=\frac{−\mathrm{3}\pm\sqrt{\mathrm{9}+\mathrm{280}}}{\mathrm{2}} \\ $$$${s}=\mathrm{7},\:−\mathrm{10} \\ $$$${from}\:\left({ii}\right) \\ $$$${s}=\frac{\mathrm{3}\pm\sqrt{\mathrm{9}+\mathrm{112}}}{\mathrm{2}} \\ $$$${s}=\mathrm{7},\:−\mathrm{4} \\ $$$${Hence} \\ $$$${s}=\mathrm{7} \\ $$$${x}−{y}=\mathrm{2}{s}=\mathrm{14} \\ $$
Answered by Rasheed.Sindhi last updated on 16/Apr/21
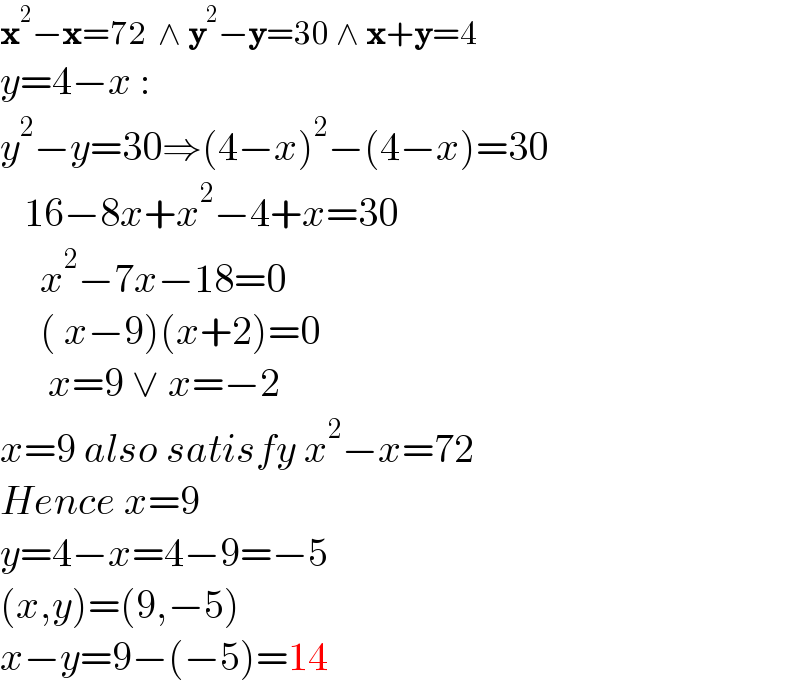
$$\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\boldsymbol{\mathrm{x}}=\mathrm{72}\:\:\wedge\:\boldsymbol{\mathrm{y}}^{\mathrm{2}} −\boldsymbol{\mathrm{y}}=\mathrm{30}\:\wedge\:\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}=\mathrm{4} \\ $$$${y}=\mathrm{4}−{x}\:: \\ $$$${y}^{\mathrm{2}} −{y}=\mathrm{30}\Rightarrow\left(\mathrm{4}−{x}\right)^{\mathrm{2}} −\left(\mathrm{4}−{x}\right)=\mathrm{30} \\ $$$$\:\:\:\mathrm{16}−\mathrm{8}{x}+{x}^{\mathrm{2}} −\mathrm{4}+{x}=\mathrm{30} \\ $$$$\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{18}=\mathrm{0} \\ $$$$\:\:\:\:\:\left(\:{x}−\mathrm{9}\right)\left({x}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:{x}=\mathrm{9}\:\vee\:{x}=−\mathrm{2}\: \\ $$$${x}=\mathrm{9}\:{also}\:{satisfy}\:{x}^{\mathrm{2}} −{x}=\mathrm{72} \\ $$$${Hence}\:{x}=\mathrm{9} \\ $$$${y}=\mathrm{4}−{x}=\mathrm{4}−\mathrm{9}=−\mathrm{5} \\ $$$$\left({x},{y}\right)=\left(\mathrm{9},−\mathrm{5}\right) \\ $$$${x}−{y}=\mathrm{9}−\left(−\mathrm{5}\right)=\mathrm{14} \\ $$
