Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 214499 by hardmath last updated on 10/Dec/24

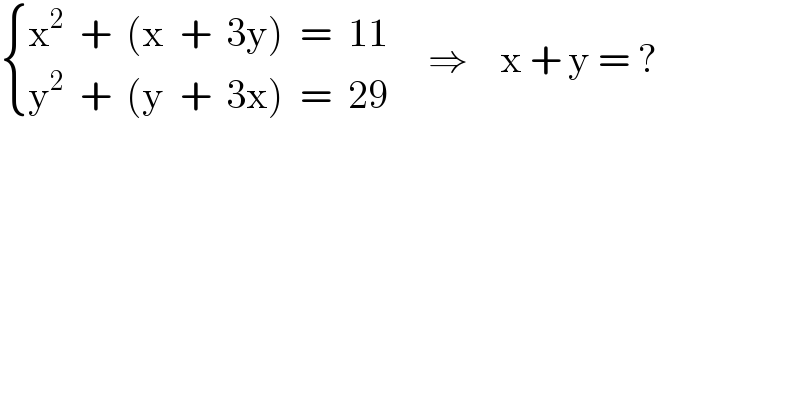
{ ((x^2 + (x + 3y) = 11)),((y^2 + (y + 3x) = 29)) :} ⇒ x + y = ?

$$\begin{cases}{\mathrm{x}^{\mathrm{2}} \:\:+\:\:\left(\mathrm{x}\:\:+\:\:\mathrm{3y}\right)\:\:=\:\:\mathrm{11}}\\{\mathrm{y}^{\mathrm{2}} \:\:+\:\:\left(\mathrm{y}\:\:+\:\:\mathrm{3x}\right)\:\:=\:\:\mathrm{29}}\end{cases}\:\:\:\:\:\Rightarrow\:\:\:\:\mathrm{x}\:+\:\mathrm{y}\:=\:? \\ $$

Commented by Frix last updated on 10/Dec/24

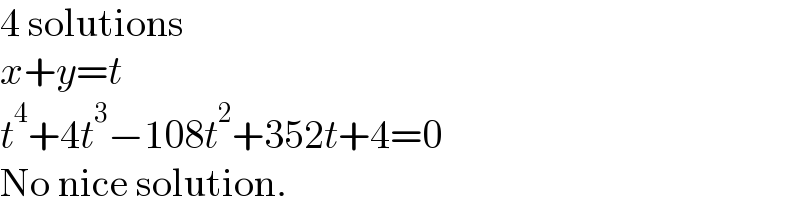
4 solutions x+y=t t^4 +4t^3 −108t^2 +352t+4=0 No nice solution.

$$\mathrm{4}\:\mathrm{solutions} \\ $$$${x}+{y}={t} \\ $$$${t}^{\mathrm{4}} +\mathrm{4}{t}^{\mathrm{3}} −\mathrm{108}{t}^{\mathrm{2}} +\mathrm{352}{t}+\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{No}\:\mathrm{nice}\:\mathrm{solution}. \\ $$

Answered by A5T last updated on 10/Dec/24

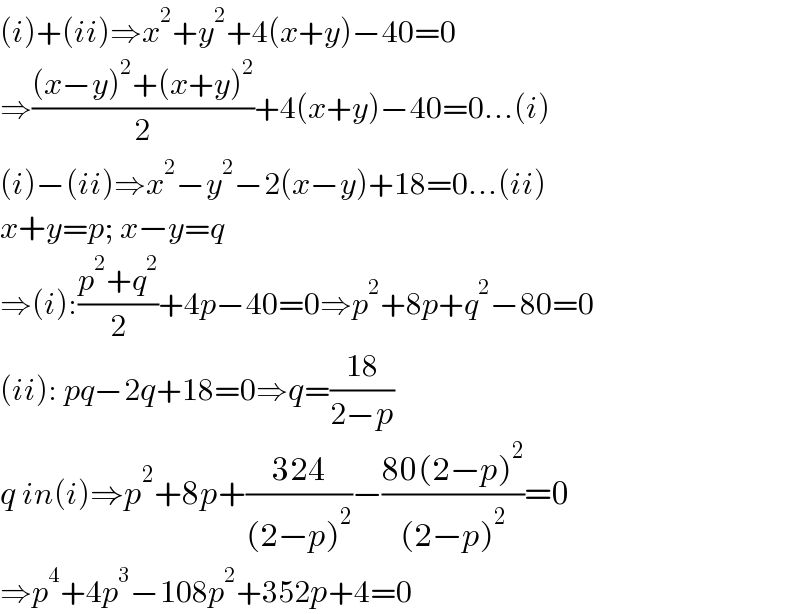
(i)+(ii)⇒x^2 +y^2 +4(x+y)−40=0 ⇒(((x−y)^2 +(x+y)^2 )/2)+4(x+y)−40=0...(i) (i)−(ii)⇒x^2 −y^2 −2(x−y)+18=0...(ii) x+y=p; x−y=q ⇒(i):((p^2 +q^2 )/2)+4p−40=0⇒p^2 +8p+q^2 −80=0 (ii): pq−2q+18=0⇒q=((18)/(2−p)) q in(i)⇒p^2 +8p+((324)/((2−p)^2 ))−((80(2−p)^2 )/((2−p)^2 ))=0 ⇒p^4 +4p^3 −108p^2 +352p+4=0

$$\left({i}\right)+\left({ii}\right)\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{4}\left({x}+{y}\right)−\mathrm{40}=\mathrm{0} \\ $$$$\Rightarrow\frac{\left({x}−{y}\right)^{\mathrm{2}} +\left({x}+{y}\right)^{\mathrm{2}} }{\mathrm{2}}+\mathrm{4}\left({x}+{y}\right)−\mathrm{40}=\mathrm{0}...\left({i}\right) \\ $$$$\left({i}\right)−\left({ii}\right)\Rightarrow{x}^{\mathrm{2}} −{y}^{\mathrm{2}} −\mathrm{2}\left({x}−{y}\right)+\mathrm{18}=\mathrm{0}...\left({ii}\right) \\ $$$${x}+{y}={p};\:{x}−{y}={q} \\ $$$$\Rightarrow\left({i}\right):\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{4}{p}−\mathrm{40}=\mathrm{0}\Rightarrow{p}^{\mathrm{2}} +\mathrm{8}{p}+{q}^{\mathrm{2}} −\mathrm{80}=\mathrm{0} \\ $$$$\left({ii}\right):\:{pq}−\mathrm{2}{q}+\mathrm{18}=\mathrm{0}\Rightarrow{q}=\frac{\mathrm{18}}{\mathrm{2}−{p}} \\ $$$${q}\:{in}\left({i}\right)\Rightarrow{p}^{\mathrm{2}} +\mathrm{8}{p}+\frac{\mathrm{324}}{\left(\mathrm{2}−{p}\right)^{\mathrm{2}} }−\frac{\mathrm{80}\left(\mathrm{2}−{p}\right)^{\mathrm{2}} }{\left(\mathrm{2}−{p}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow{p}^{\mathrm{4}} +\mathrm{4}{p}^{\mathrm{3}} −\mathrm{108}{p}^{\mathrm{2}} +\mathrm{352}{p}+\mathrm{4}=\mathrm{0} \\ $$

Commented by Rasheed.Sindhi last updated on 10/Dec/24

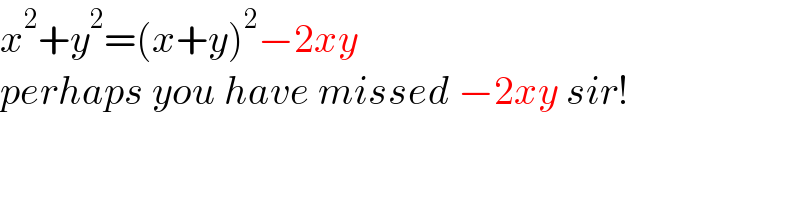
x^2 +y^2 =(x+y)^2 −2xy perhaps you have missed −2xy sir!

$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{xy} \\ $$$${perhaps}\:{you}\:{have}\:{missed}\:−\mathrm{2}{xy}\:{sir}! \\ $$

Commented by A5T last updated on 10/Dec/24

Took another path, thanks.

$${Took}\:{another}\:{path},\:{thanks}. \\ $$

Answered by Rasheed.Sindhi last updated on 11/Dec/24

{ ((x^2 + (x + 3y) = 11)),((y^2 + (y + 3x) = 29)) :} ⇒ x + y = ? Adding: x^2 +y^2 +(x+y)+3(x+y)=40 (x+y)^2 −2xy+4(x+y)=40 but xy=(1/4){(x+y)^2 −(x−y)^2 } (x+y)^2 −2[(1/4){(x+y)^2 −(x−y)^2 }]+4(x+y)=40 let x+y=a,x−y=b a^2 −(1/2){a^2 −b^2 }+4a=40 a^2 +b^2 +8a=80......(i) Subtracting: x^2 −y^2 +(x−y)−3(x−y)=−18 (x−y)(x+y)−2(x−y)=−18 (x−y)(x+y−2)=−18 b(a−2)=−18.........(ii) b=((18)/(2−a)) putting this in (i) a^2 +(((18)/(2−a)))^2 +8a=80 a^2 (2−a)^2 +324+8a(2−a)^2 =80(2−a)^2 a^2 (a^2 −4a+4)+324+8a(a^2 −4a+4)=80a^2 −320a+320 a^2 (a^2 −4a+4)+324+8a(a^2 −4a+4)=80a^2 −320a+320 a^4 −4a^3 +4a^2 +8a^3 −32a^2 +32a+324−80a^2 +320a−320=0 a^4 +4a^3 −108a^2 +352a+4 ....

$$\begin{cases}{\mathrm{x}^{\mathrm{2}} \:\:+\:\:\left(\mathrm{x}\:\:+\:\:\mathrm{3y}\right)\:\:=\:\:\mathrm{11}}\\{\mathrm{y}^{\mathrm{2}} \:\:+\:\:\left(\mathrm{y}\:\:+\:\:\mathrm{3x}\right)\:\:=\:\:\mathrm{29}}\end{cases}\:\:\:\:\:\Rightarrow\:\:\:\:\mathrm{x}\:+\:\mathrm{y}\:=\:? \\ $$$$\mathrm{Adding}: \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{3}\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{40} \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\mathrm{2xy}+\mathrm{4}\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{40} \\ $$$$\mathrm{but}\:\mathrm{xy}=\frac{\mathrm{1}}{\mathrm{4}}\left\{\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} \right\} \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{4}}\left\{\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{2}} \right\}\right]+\mathrm{4}\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{40} \\ $$$$\mathrm{let}\:\mathrm{x}+\mathrm{y}=\mathrm{a},\mathrm{x}−\mathrm{y}=\mathrm{b} \\ $$$$\mathrm{a}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right\}+\mathrm{4a}=\mathrm{40} \\ $$$$\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{8a}=\mathrm{80}......\left(\mathrm{i}\right) \\ $$$$\mathrm{Subtracting}: \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} +\left(\mathrm{x}−\mathrm{y}\right)−\mathrm{3}\left(\mathrm{x}−\mathrm{y}\right)=−\mathrm{18} \\ $$$$\left(\mathrm{x}−\mathrm{y}\right)\left(\mathrm{x}+\mathrm{y}\right)−\mathrm{2}\left(\mathrm{x}−\mathrm{y}\right)=−\mathrm{18} \\ $$$$\left(\mathrm{x}−\mathrm{y}\right)\left(\mathrm{x}+\mathrm{y}−\mathrm{2}\right)=−\mathrm{18} \\ $$$$\mathrm{b}\left(\mathrm{a}−\mathrm{2}\right)=−\mathrm{18}.........\left(\mathrm{ii}\right) \\ $$$$\mathrm{b}=\frac{\mathrm{18}}{\mathrm{2}−\mathrm{a}} \\ $$$$\mathrm{putting}\:\mathrm{this}\:\mathrm{in}\:\left(\mathrm{i}\right) \\ $$$$\mathrm{a}^{\mathrm{2}} +\left(\frac{\mathrm{18}}{\mathrm{2}−\mathrm{a}}\right)^{\mathrm{2}} +\mathrm{8a}=\mathrm{80} \\ $$$$\mathrm{a}^{\mathrm{2}} \left(\mathrm{2}−\mathrm{a}\right)^{\mathrm{2}} +\mathrm{324}+\mathrm{8a}\left(\mathrm{2}−{a}\right)^{\mathrm{2}} =\mathrm{80}\left(\mathrm{2}−\mathrm{a}\right)^{\mathrm{2}} \\ $$$$\mathrm{a}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} −\mathrm{4a}+\mathrm{4}\right)+\mathrm{324}+\mathrm{8a}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{4a}+\mathrm{4}\right)=\mathrm{80a}^{\mathrm{2}} −\mathrm{320a}+\mathrm{320} \\ $$$$\mathrm{a}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} −\mathrm{4a}+\mathrm{4}\right)+\mathrm{324}+\mathrm{8a}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{4a}+\mathrm{4}\right)=\mathrm{80a}^{\mathrm{2}} −\mathrm{320a}+\mathrm{320} \\ $$$$\mathrm{a}^{\mathrm{4}} −\mathrm{4a}^{\mathrm{3}} +\mathrm{4a}^{\mathrm{2}} +\mathrm{8a}^{\mathrm{3}} −\mathrm{32a}^{\mathrm{2}} +\mathrm{32a}+\mathrm{324}−\mathrm{80a}^{\mathrm{2}} +\mathrm{320a}−\mathrm{320}=\mathrm{0} \\ $$$$\mathrm{a}^{\mathrm{4}} +\mathrm{4a}^{\mathrm{3}} −\mathrm{108a}^{\mathrm{2}} +\mathrm{352a}+\mathrm{4} \\ $$$$.... \\ $$

Commented by A5T last updated on 10/Dec/24

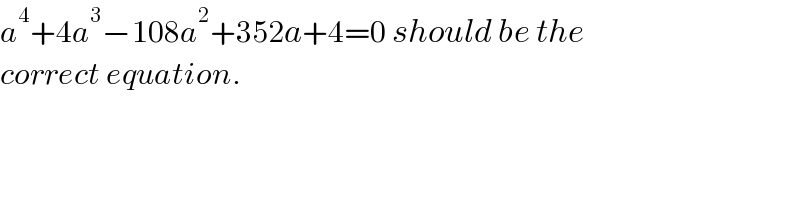
a^4 +4a^3 −108a^2 +352a+4=0 should be the correct equation.

$${a}^{\mathrm{4}} +\mathrm{4}{a}^{\mathrm{3}} −\mathrm{108}{a}^{\mathrm{2}} +\mathrm{352}{a}+\mathrm{4}=\mathrm{0}\:{should}\:{be}\:{the}\: \\ $$$${correct}\:{equation}. \\ $$

Answered by ajfour last updated on 11/Dec/24

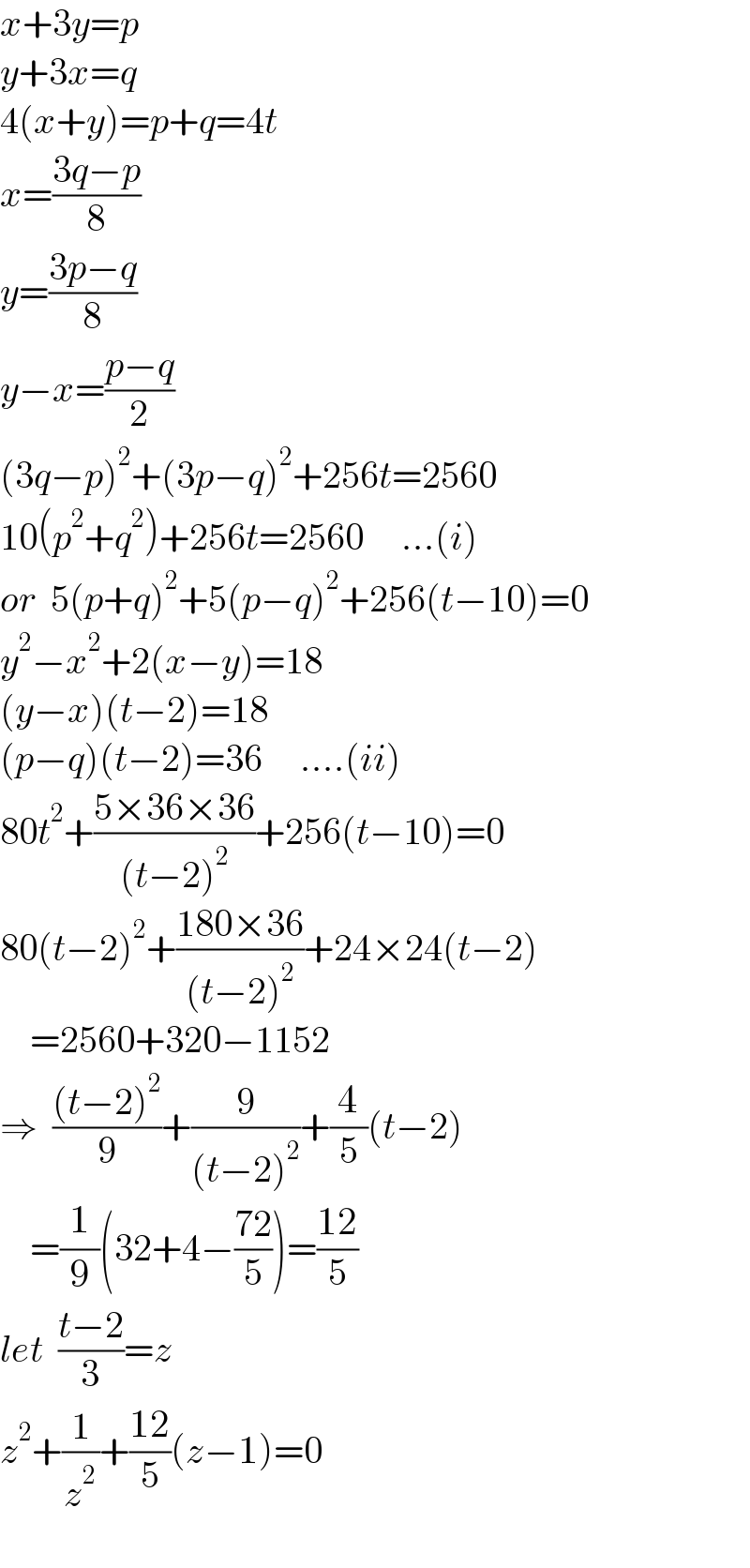
x+3y=p y+3x=q 4(x+y)=p+q=4t x=((3q−p)/8) y=((3p−q)/8) y−x=((p−q)/2) (3q−p)^2 +(3p−q)^2 +256t=2560 10(p^2 +q^2 )+256t=2560 ...(i) or 5(p+q)^2 +5(p−q)^2 +256(t−10)=0 y^2 −x^2 +2(x−y)=18 (y−x)(t−2)=18 (p−q)(t−2)=36 ....(ii) 80t^2 +((5×36×36)/((t−2)^2 ))+256(t−10)=0 80(t−2)^2 +((180×36)/((t−2)^2 ))+24×24(t−2) =2560+320−1152 ⇒ (((t−2)^2 )/9)+(9/((t−2)^2 ))+(4/5)(t−2) =(1/9)(32+4−((72)/5))=((12)/5) let ((t−2)/3)=z z^2 +(1/z^2 )+((12)/5)(z−1)=0

$${x}+\mathrm{3}{y}={p} \\ $$$${y}+\mathrm{3}{x}={q} \\ $$$$\mathrm{4}\left({x}+{y}\right)={p}+{q}=\mathrm{4}{t} \\ $$$${x}=\frac{\mathrm{3}{q}−{p}}{\mathrm{8}} \\ $$$${y}=\frac{\mathrm{3}{p}−{q}}{\mathrm{8}} \\ $$$${y}−{x}=\frac{{p}−{q}}{\mathrm{2}} \\ $$$$\left(\mathrm{3}{q}−{p}\right)^{\mathrm{2}} +\left(\mathrm{3}{p}−{q}\right)^{\mathrm{2}} +\mathrm{256}{t}=\mathrm{2560} \\ $$$$\mathrm{10}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)+\mathrm{256}{t}=\mathrm{2560}\:\:\:\:\:...\left({i}\right) \\ $$$${or}\:\:\mathrm{5}\left({p}+{q}\right)^{\mathrm{2}} +\mathrm{5}\left({p}−{q}\right)^{\mathrm{2}} +\mathrm{256}\left({t}−\mathrm{10}\right)=\mathrm{0} \\ $$$${y}^{\mathrm{2}} −{x}^{\mathrm{2}} +\mathrm{2}\left({x}−{y}\right)=\mathrm{18} \\ $$$$\left({y}−{x}\right)\left({t}−\mathrm{2}\right)=\mathrm{18} \\ $$$$\left({p}−{q}\right)\left({t}−\mathrm{2}\right)=\mathrm{36}\:\:\:\:\:....\left({ii}\right) \\ $$$$\mathrm{80}{t}^{\mathrm{2}} +\frac{\mathrm{5}×\mathrm{36}×\mathrm{36}}{\left({t}−\mathrm{2}\right)^{\mathrm{2}} }+\mathrm{256}\left({t}−\mathrm{10}\right)=\mathrm{0} \\ $$$$\mathrm{80}\left({t}−\mathrm{2}\right)^{\mathrm{2}} +\frac{\mathrm{180}×\mathrm{36}}{\left({t}−\mathrm{2}\right)^{\mathrm{2}} }+\mathrm{24}×\mathrm{24}\left({t}−\mathrm{2}\right) \\ $$$$\:\:\:\:=\mathrm{2560}+\mathrm{320}−\mathrm{1152} \\ $$$$\Rightarrow\:\:\frac{\left({t}−\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{9}}+\frac{\mathrm{9}}{\left({t}−\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{5}}\left({t}−\mathrm{2}\right) \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{32}+\mathrm{4}−\frac{\mathrm{72}}{\mathrm{5}}\right)=\frac{\mathrm{12}}{\mathrm{5}} \\ $$$${let}\:\:\frac{{t}−\mathrm{2}}{\mathrm{3}}={z} \\ $$$${z}^{\mathrm{2}} +\frac{\mathrm{1}}{{z}^{\mathrm{2}} }+\frac{\mathrm{12}}{\mathrm{5}}\left({z}−\mathrm{1}\right)=\mathrm{0} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com