
Question Number 187091 by Humble last updated on 13/Feb/23
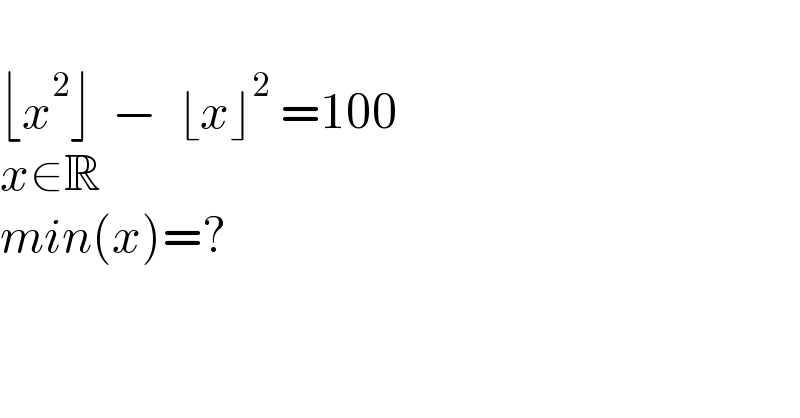
$$ \\ $$$$\lfloor{x}^{\mathrm{2}} \rfloor\:\:−\:\:\lfloor{x}\rfloor^{\mathrm{2}} \:=\mathrm{100} \\ $$$${x}\in\mathbb{R} \\ $$$${min}\left({x}\right)=? \\ $$
Answered by MJS_new last updated on 13/Feb/23
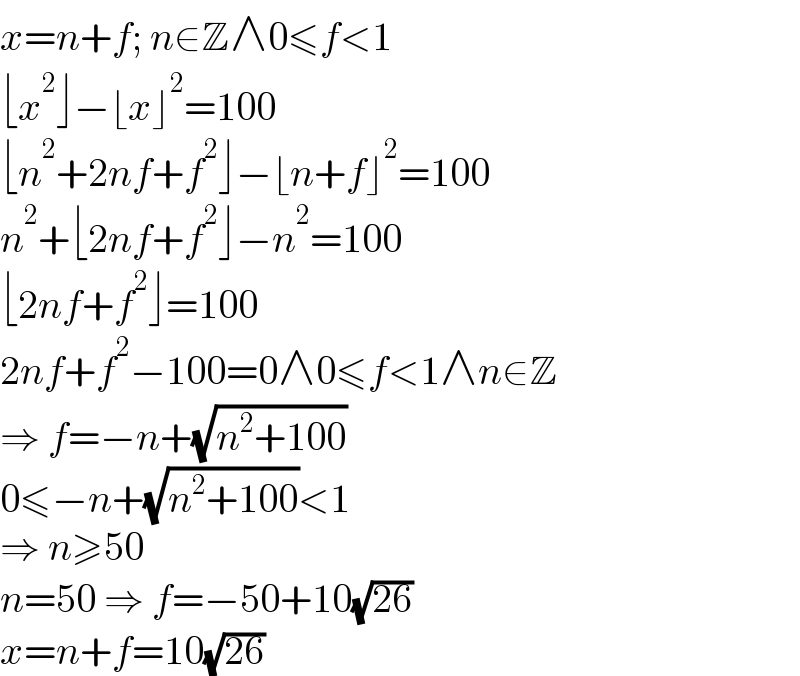
$${x}={n}+{f};\:{n}\in\mathbb{Z}\wedge\mathrm{0}\leqslant{f}<\mathrm{1} \\ $$$$\lfloor{x}^{\mathrm{2}} \rfloor−\lfloor{x}\rfloor^{\mathrm{2}} =\mathrm{100} \\ $$$$\lfloor{n}^{\mathrm{2}} +\mathrm{2}{nf}+{f}^{\mathrm{2}} \rfloor−\lfloor{n}+{f}\rfloor^{\mathrm{2}} =\mathrm{100} \\ $$$${n}^{\mathrm{2}} +\lfloor\mathrm{2}{nf}+{f}^{\mathrm{2}} \rfloor−{n}^{\mathrm{2}} =\mathrm{100} \\ $$$$\lfloor\mathrm{2}{nf}+{f}^{\mathrm{2}} \rfloor=\mathrm{100} \\ $$$$\mathrm{2}{nf}+{f}^{\mathrm{2}} −\mathrm{100}=\mathrm{0}\wedge\mathrm{0}\leqslant{f}<\mathrm{1}\wedge{n}\in\mathbb{Z} \\ $$$$\Rightarrow\:{f}=−{n}+\sqrt{{n}^{\mathrm{2}} +\mathrm{100}} \\ $$$$\mathrm{0}\leqslant−{n}+\sqrt{{n}^{\mathrm{2}} +\mathrm{100}}<\mathrm{1} \\ $$$$\Rightarrow\:{n}\geqslant\mathrm{50} \\ $$$${n}=\mathrm{50}\:\Rightarrow\:{f}=−\mathrm{50}+\mathrm{10}\sqrt{\mathrm{26}} \\ $$$${x}={n}+{f}=\mathrm{10}\sqrt{\mathrm{26}} \\ $$
Commented by Humble last updated on 13/Feb/23
$${thank}\:{you},\:{sir} \\ $$
Commented by MJS_new last updated on 13/Feb/23

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$
Answered by mr W last updated on 13/Feb/23
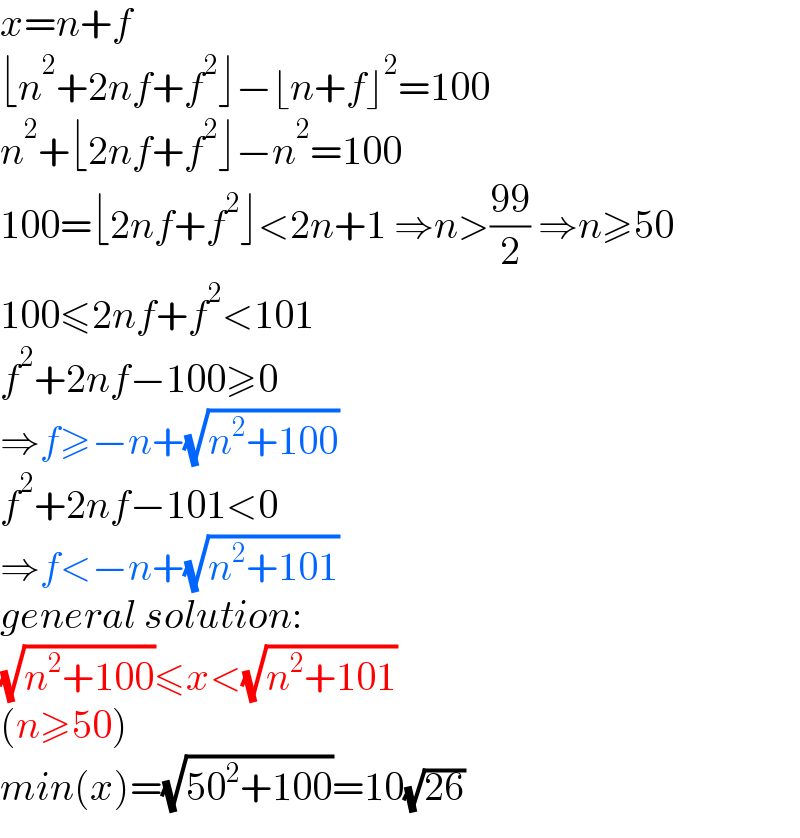
$${x}={n}+{f} \\ $$$$\lfloor{n}^{\mathrm{2}} +\mathrm{2}{nf}+{f}^{\mathrm{2}} \rfloor−\lfloor{n}+{f}\rfloor^{\mathrm{2}} =\mathrm{100} \\ $$$${n}^{\mathrm{2}} +\lfloor\mathrm{2}{nf}+{f}^{\mathrm{2}} \rfloor−{n}^{\mathrm{2}} =\mathrm{100} \\ $$$$\mathrm{100}=\lfloor\mathrm{2}{nf}+{f}^{\mathrm{2}} \rfloor<\mathrm{2}{n}+\mathrm{1}\:\Rightarrow{n}>\frac{\mathrm{99}}{\mathrm{2}}\:\Rightarrow{n}\geqslant\mathrm{50} \\ $$$$\mathrm{100}\leqslant\mathrm{2}{nf}+{f}^{\mathrm{2}} <\mathrm{101} \\ $$$${f}^{\mathrm{2}} +\mathrm{2}{nf}−\mathrm{100}\geqslant\mathrm{0} \\ $$$$\Rightarrow{f}\geqslant−{n}+\sqrt{{n}^{\mathrm{2}} +\mathrm{100}} \\ $$$${f}^{\mathrm{2}} +\mathrm{2}{nf}−\mathrm{101}<\mathrm{0} \\ $$$$\Rightarrow{f}<−{n}+\sqrt{{n}^{\mathrm{2}} +\mathrm{101}} \\ $$$${general}\:{solution}: \\ $$$$\sqrt{{n}^{\mathrm{2}} +\mathrm{100}}\leqslant{x}<\sqrt{{n}^{\mathrm{2}} +\mathrm{101}} \\ $$$$\left({n}\geqslant\mathrm{50}\right) \\ $$$${min}\left({x}\right)=\sqrt{\mathrm{50}^{\mathrm{2}} +\mathrm{100}}=\mathrm{10}\sqrt{\mathrm{26}} \\ $$
Commented by Humble last updated on 13/Feb/23

$${thank}\:{you},\:{Boss}. \\ $$
Commented by mr W last updated on 13/Feb/23

$${you}\:{too}! \\ $$
