
Question Number 195121 by mathlove last updated on 25/Jul/23
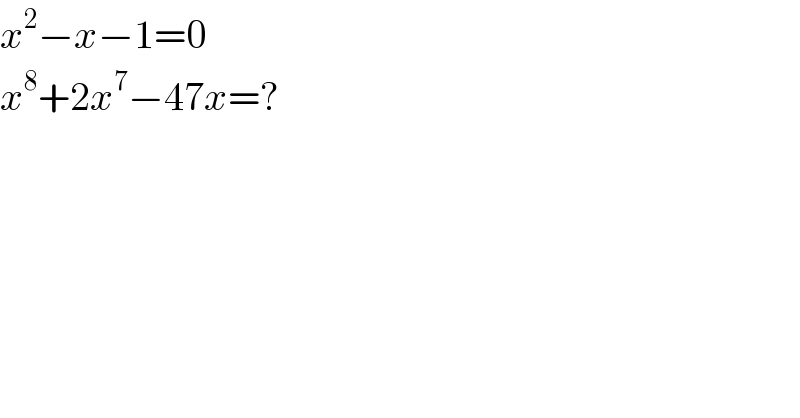
$${x}^{\mathrm{2}} −{x}−\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{8}} +\mathrm{2}{x}^{\mathrm{7}} −\mathrm{47}{x}=? \\ $$
Answered by qaz last updated on 25/Jul/23
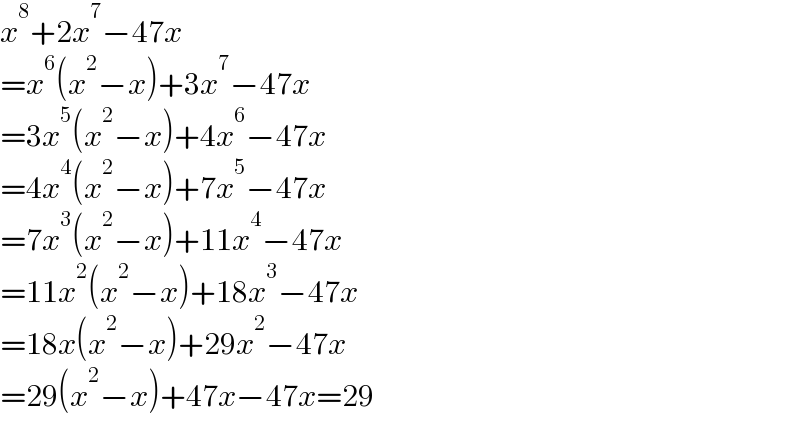
$${x}^{\mathrm{8}} +\mathrm{2}{x}^{\mathrm{7}} −\mathrm{47}{x} \\ $$$$={x}^{\mathrm{6}} \left({x}^{\mathrm{2}} −{x}\right)+\mathrm{3}{x}^{\mathrm{7}} −\mathrm{47}{x} \\ $$$$=\mathrm{3}{x}^{\mathrm{5}} \left({x}^{\mathrm{2}} −{x}\right)+\mathrm{4}{x}^{\mathrm{6}} −\mathrm{47}{x} \\ $$$$=\mathrm{4}{x}^{\mathrm{4}} \left({x}^{\mathrm{2}} −{x}\right)+\mathrm{7}{x}^{\mathrm{5}} −\mathrm{47}{x} \\ $$$$=\mathrm{7}{x}^{\mathrm{3}} \left({x}^{\mathrm{2}} −{x}\right)+\mathrm{11}{x}^{\mathrm{4}} −\mathrm{47}{x} \\ $$$$=\mathrm{11}{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −{x}\right)+\mathrm{18}{x}^{\mathrm{3}} −\mathrm{47}{x} \\ $$$$=\mathrm{18}{x}\left({x}^{\mathrm{2}} −{x}\right)+\mathrm{29}{x}^{\mathrm{2}} −\mathrm{47}{x} \\ $$$$=\mathrm{29}\left({x}^{\mathrm{2}} −{x}\right)+\mathrm{47}{x}−\mathrm{47}{x}=\mathrm{29} \\ $$
Answered by Rasheed.Sindhi last updated on 25/Jul/23
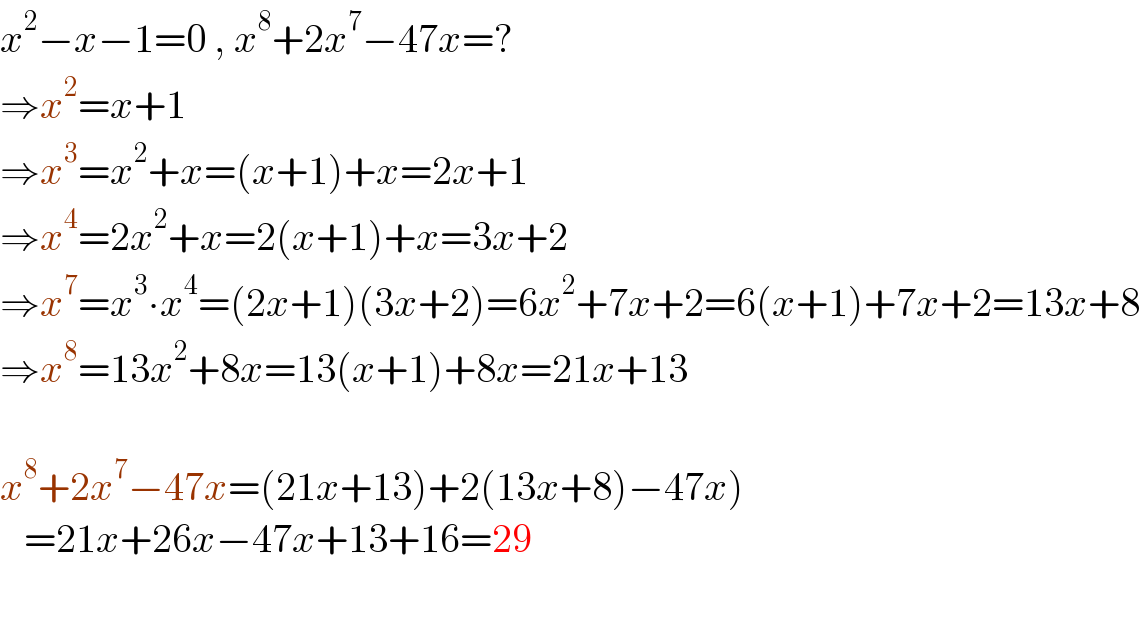
$${x}^{\mathrm{2}} −{x}−\mathrm{1}=\mathrm{0}\:,\:{x}^{\mathrm{8}} +\mathrm{2}{x}^{\mathrm{7}} −\mathrm{47}{x}=? \\ $$$$\Rightarrow{x}^{\mathrm{2}} ={x}+\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{3}} ={x}^{\mathrm{2}} +{x}=\left({x}+\mathrm{1}\right)+{x}=\mathrm{2}{x}+\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{4}} =\mathrm{2}{x}^{\mathrm{2}} +{x}=\mathrm{2}\left({x}+\mathrm{1}\right)+{x}=\mathrm{3}{x}+\mathrm{2} \\ $$$$\Rightarrow{x}^{\mathrm{7}} ={x}^{\mathrm{3}} \centerdot{x}^{\mathrm{4}} =\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{3}{x}+\mathrm{2}\right)=\mathrm{6}{x}^{\mathrm{2}} +\mathrm{7}{x}+\mathrm{2}=\mathrm{6}\left({x}+\mathrm{1}\right)+\mathrm{7}{x}+\mathrm{2}=\mathrm{13}{x}+\mathrm{8} \\ $$$$\Rightarrow{x}^{\mathrm{8}} =\mathrm{13}{x}^{\mathrm{2}} +\mathrm{8}{x}=\mathrm{13}\left({x}+\mathrm{1}\right)+\mathrm{8}{x}=\mathrm{21}{x}+\mathrm{13} \\ $$$$\: \\ $$$$\left.{x}^{\mathrm{8}} +\mathrm{2}{x}^{\mathrm{7}} −\mathrm{47}{x}=\left(\mathrm{21}{x}+\mathrm{13}\right)+\mathrm{2}\left(\mathrm{13}{x}+\mathrm{8}\right)−\mathrm{47}{x}\right) \\ $$$$\:\:\:=\mathrm{21}{x}+\mathrm{26}{x}−\mathrm{47}{x}+\mathrm{13}+\mathrm{16}=\mathrm{29} \\ $$$$\:\: \\ $$
