Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 218099 by Rasheed.Sindhi last updated on 29/Mar/25

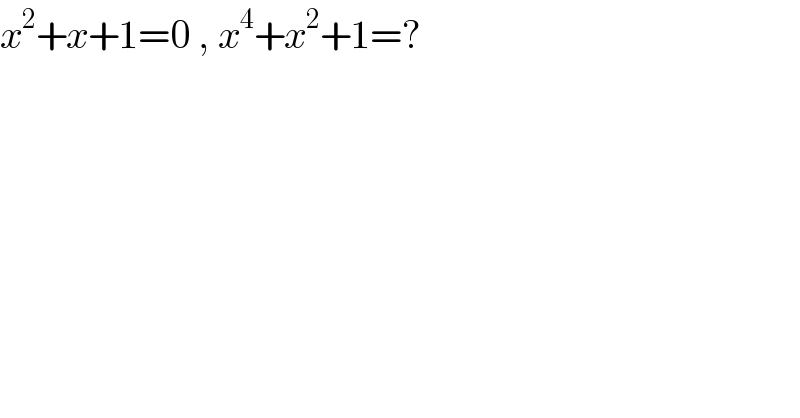
x^2 +x+1=0 , x^4 +x^2 +1=?

$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}\:,\:{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}=? \\ $$

Answered by Rasheed.Sindhi last updated on 29/Mar/25

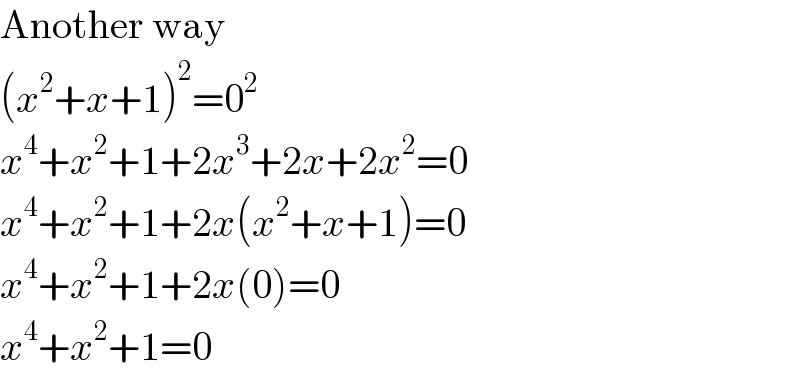
Another way (x^2 +x+1)^2 =0^2 x^4 +x^2 +1+2x^3 +2x+2x^2 =0 x^4 +x^2 +1+2x(x^2 +x+1)=0 x^4 +x^2 +1+2x(0)=0 x^4 +x^2 +1=0

$$\mathrm{Another}\:\mathrm{way} \\ $$$$\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0}^{\mathrm{2}} \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{x}^{\mathrm{3}} +\mathrm{2}{x}+\mathrm{2}{x}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{x}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{x}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$

Answered by profcedricjunior last updated on 29/Mar/25

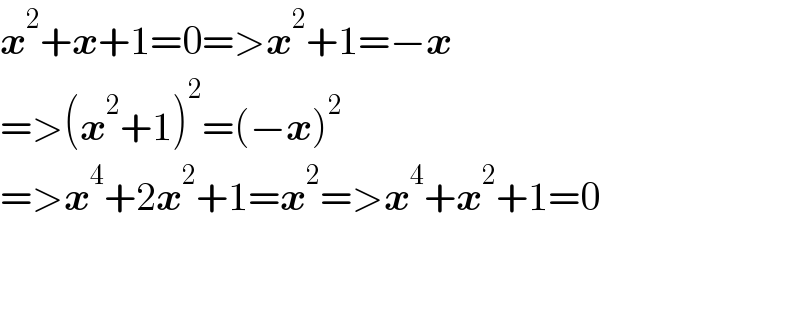
x^2 +x+1=0=>x^2 +1=−x =>(x^2 +1)^2 =(−x)^2 =>x^4 +2x^2 +1=x^2 =>x^4 +x^2 +1=0

$$\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{x}}+\mathrm{1}=\mathrm{0}=>\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}=−\boldsymbol{{x}} \\ $$$$=>\left(\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} =\left(−\boldsymbol{{x}}\right)^{\mathrm{2}} \\ $$$$=>\boldsymbol{{x}}^{\mathrm{4}} +\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}=\boldsymbol{{x}}^{\mathrm{2}} =>\boldsymbol{{x}}^{\mathrm{4}} +\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$

Answered by ArshadS last updated on 29/Mar/25

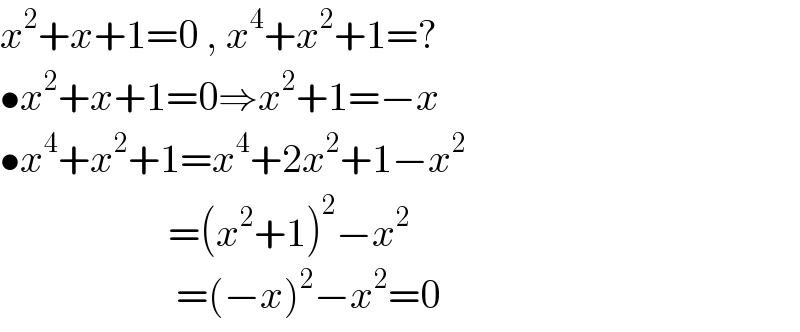
x^2 +x+1=0 , x^4 +x^2 +1=? •x^2 +x+1=0⇒x^2 +1=−x •x^4 +x^2 +1=x^4 +2x^2 +1−x^2 =(x^2 +1)^2 −x^2 =(−x)^2 −x^2 =0

$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}\:,\:{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}=? \\ $$$$\bullet{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}\Rightarrow{x}^{\mathrm{2}} +\mathrm{1}=−{x} \\ $$$$\bullet{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}={x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}−{x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(−{x}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} =\mathrm{0} \\ $$

Answered by ArshadS last updated on 30/Mar/25

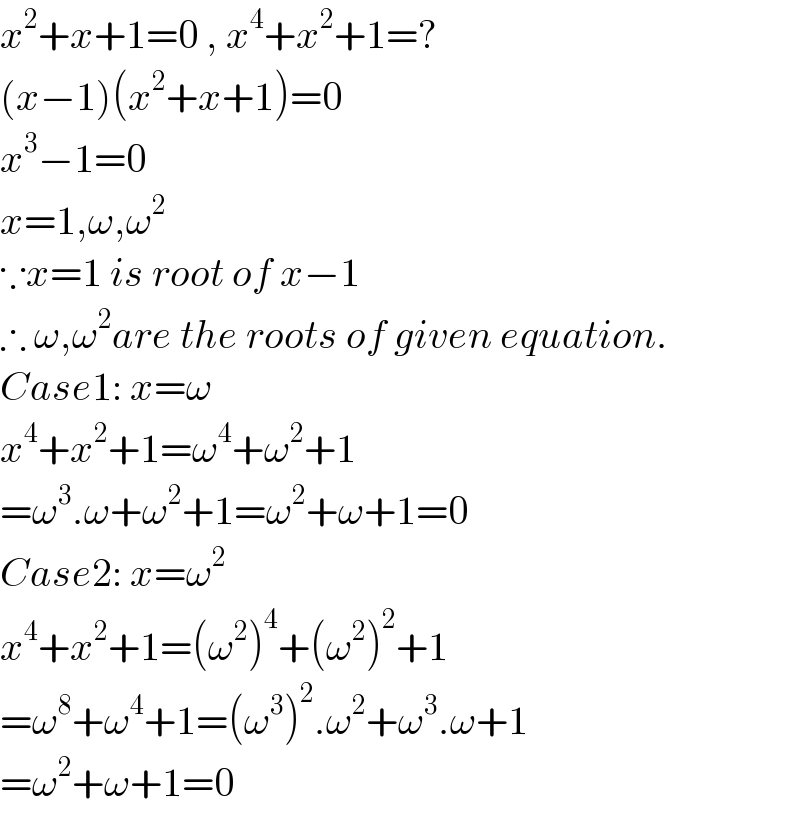
x^2 +x+1=0 , x^4 +x^2 +1=? (x−1)(x^2 +x+1)=0 x^3 −1=0 x=1,ω,ω^2 ∵x=1 is root of x−1 ∴ ω,ω^2 are the roots of given equation. Case1: x=ω x^4 +x^2 +1=ω^4 +ω^2 +1 =ω^3 .ω+ω^2 +1=ω^2 +ω+1=0 Case2: x=ω^2 x^4 +x^2 +1=(ω^2 )^4 +(ω^2 )^2 +1 =ω^8 +ω^4 +1=(ω^3 )^2 .ω^2 +ω^3 .ω+1 =ω^2 +ω+1=0

$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}\:,\:{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}=? \\ $$$$\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\mathrm{1}=\mathrm{0} \\ $$$${x}=\mathrm{1},\omega,\omega^{\mathrm{2}} \\ $$$$\because{x}=\mathrm{1}\:{is}\:{root}\:{of}\:{x}−\mathrm{1} \\ $$$$\therefore\:\omega,\omega^{\mathrm{2}} {are}\:{the}\:{roots}\:{of}\:{given}\:{equation}. \\ $$$${Case}\mathrm{1}:\:{x}=\omega \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}=\omega^{\mathrm{4}} +\omega^{\mathrm{2}} +\mathrm{1} \\ $$$$=\omega^{\mathrm{3}} .\omega+\omega^{\mathrm{2}} +\mathrm{1}=\omega^{\mathrm{2}} +\omega+\mathrm{1}=\mathrm{0} \\ $$$${Case}\mathrm{2}:\:{x}=\omega^{\mathrm{2}} \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}=\left(\omega^{\mathrm{2}} \right)^{\mathrm{4}} +\left(\omega^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{1} \\ $$$$=\omega^{\mathrm{8}} +\omega^{\mathrm{4}} +\mathrm{1}=\left(\omega^{\mathrm{3}} \right)^{\mathrm{2}} .\omega^{\mathrm{2}} +\omega^{\mathrm{3}} .\omega+\mathrm{1} \\ $$$$=\omega^{\mathrm{2}} +\omega+\mathrm{1}=\mathrm{0} \\ $$

Answered by MATHEMATICSAM last updated on 30/Mar/25

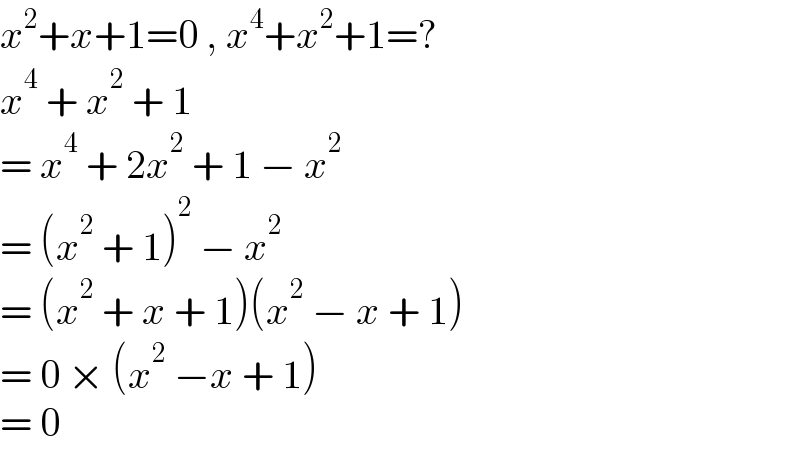
x^2 +x+1=0 , x^4 +x^2 +1=? x^4 + x^2 + 1 = x^4 + 2x^2 + 1 − x^2 = (x^2 + 1)^2 − x^2 = (x^2 + x + 1)(x^2 − x + 1) = 0 × (x^2 −x + 1) = 0

$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}\:,\:{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}=? \\ $$$${x}^{\mathrm{4}} \:+\:{x}^{\mathrm{2}} \:+\:\mathrm{1} \\ $$$$=\:{x}^{\mathrm{4}} \:+\:\mathrm{2}{x}^{\mathrm{2}} \:+\:\mathrm{1}\:−\:{x}^{\mathrm{2}} \\ $$$$=\:\left({x}^{\mathrm{2}} \:+\:\mathrm{1}\right)^{\mathrm{2}} \:−\:{x}^{\mathrm{2}} \\ $$$$=\:\left({x}^{\mathrm{2}} \:+\:{x}\:+\:\mathrm{1}\right)\left({x}^{\mathrm{2}} \:−\:{x}\:+\:\mathrm{1}\right) \\ $$$$=\:\mathrm{0}\:×\:\left({x}^{\mathrm{2}} \:−{x}\:+\:\mathrm{1}\right) \\ $$$$=\:\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com