
Question Number 199903 by frankpenredpen last updated on 11/Nov/23
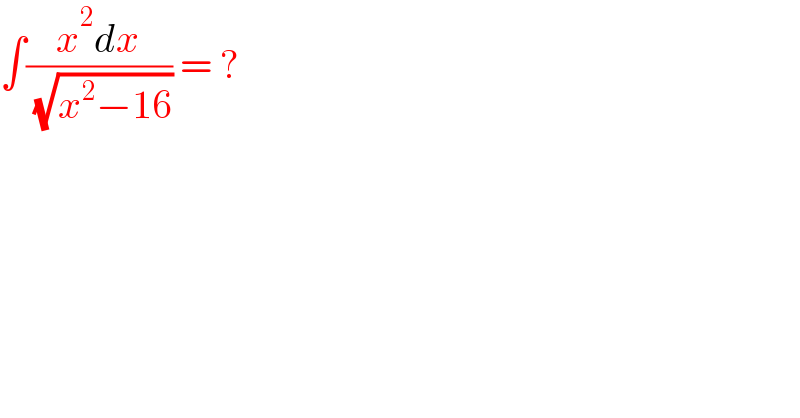
$$\int\frac{{x}^{\mathrm{2}} {dx}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{16}}}\:=\:? \\ $$
Commented by cortano12 last updated on 11/Nov/23

$$\mathrm{why}\:\partial\mathrm{x}\:? \\ $$
Answered by frankpenredpen last updated on 11/Nov/23
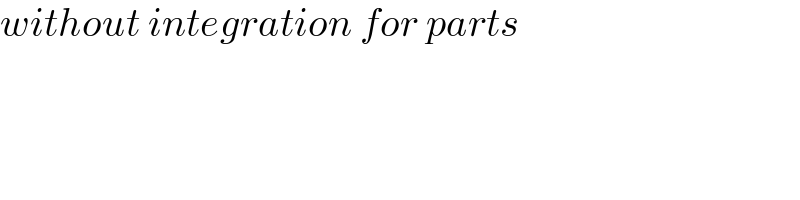
$${without}\:{integration}\:{for}\:{parts} \\ $$
Answered by Frix last updated on 11/Nov/23
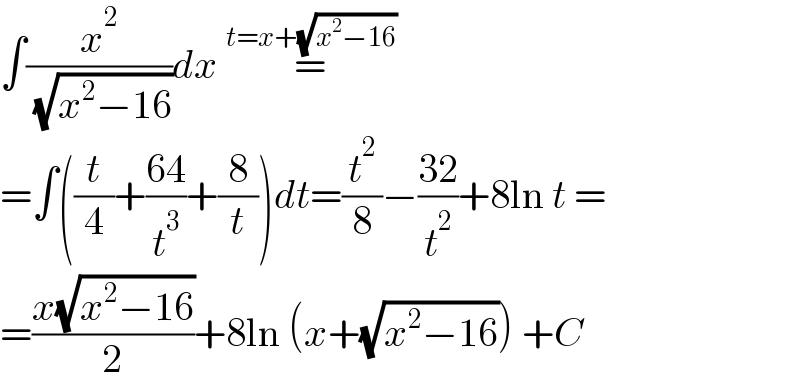
$$\int\frac{{x}^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{16}}}{dx}\:\overset{{t}={x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{16}}} {=} \\ $$$$=\int\left(\frac{{t}}{\mathrm{4}}+\frac{\mathrm{64}}{{t}^{\mathrm{3}} }+\frac{\mathrm{8}}{{t}}\right){dt}=\frac{{t}^{\mathrm{2}} }{\mathrm{8}}−\frac{\mathrm{32}}{{t}^{\mathrm{2}} }+\mathrm{8ln}\:{t}\:= \\ $$$$=\frac{{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{16}}}{\mathrm{2}}+\mathrm{8ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{16}}\right)\:+{C} \\ $$
