
Question Number 190730 by 073 last updated on 10/Apr/23
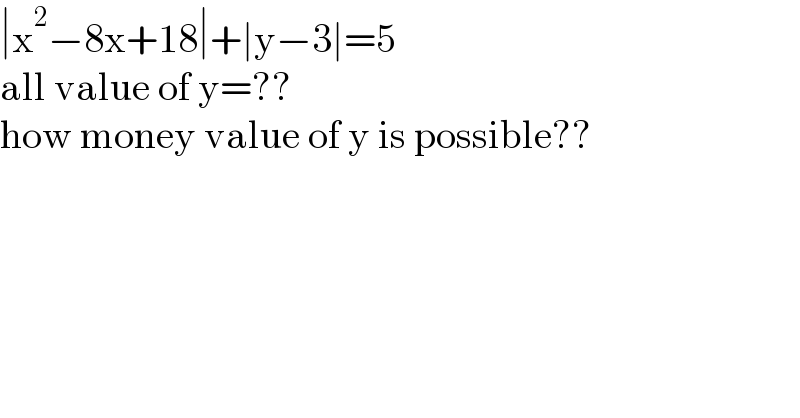
$$\mid\mathrm{x}^{\mathrm{2}} −\mathrm{8x}+\mathrm{18}\mid+\mid\mathrm{y}−\mathrm{3}\mid=\mathrm{5} \\ $$$$\mathrm{all}\:\mathrm{value}\:\mathrm{of}\:\mathrm{y}=?? \\ $$$$\mathrm{how}\:\mathrm{money}\:\mathrm{value}\:\mathrm{of}\:\mathrm{y}\:\mathrm{is}\:\mathrm{possible}?? \\ $$
Answered by Frix last updated on 10/Apr/23
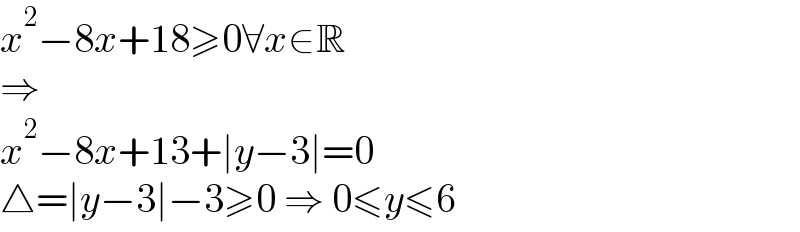
$${x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{18}\geqslant\mathrm{0}\forall{x}\in\mathbb{R} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{13}+\mid{y}−\mathrm{3}\mid=\mathrm{0} \\ $$$$\bigtriangleup=\mid{y}−\mathrm{3}\mid−\mathrm{3}\geqslant\mathrm{0}\:\Rightarrow\:\mathrm{0}\leqslant{y}\leqslant\mathrm{6} \\ $$
Commented by 073 last updated on 10/Apr/23

$$\mathrm{nice}\:\mathrm{solution} \\ $$
Answered by manxsol last updated on 10/Apr/23
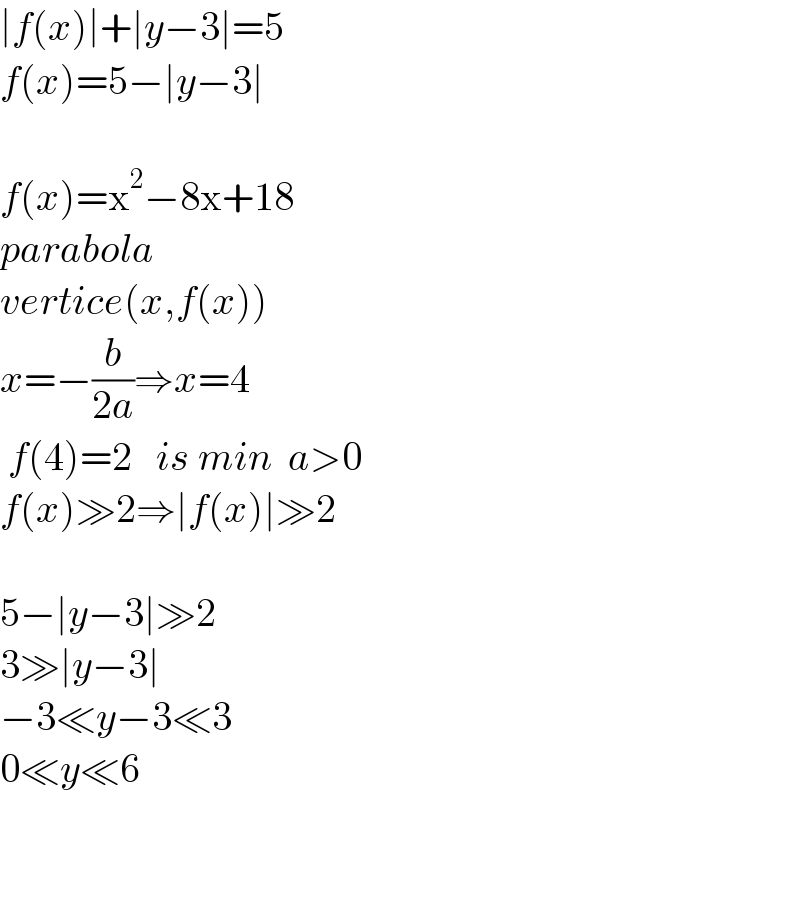
$$\mid{f}\left({x}\right)\mid+\mid{y}−\mathrm{3}\mid=\mathrm{5} \\ $$$${f}\left({x}\right)=\mathrm{5}−\mid{y}−\mathrm{3}\mid \\ $$$$ \\ $$$${f}\left({x}\right)=\mathrm{x}^{\mathrm{2}} −\mathrm{8x}+\mathrm{18} \\ $$$${parabola} \\ $$$${vertice}\left({x},{f}\left({x}\right)\right) \\ $$$${x}=−\frac{{b}}{\mathrm{2}{a}}\Rightarrow{x}=\mathrm{4}\:\:\: \\ $$$$\:{f}\left(\mathrm{4}\right)=\mathrm{2}\:\:\:{is}\:{min}\:\:{a}>\mathrm{0} \\ $$$${f}\left({x}\right)\gg\mathrm{2}\Rightarrow\mid{f}\left({x}\right)\mid\gg\mathrm{2} \\ $$$$ \\ $$$$\mathrm{5}−\mid{y}−\mathrm{3}\mid\gg\mathrm{2} \\ $$$$\mathrm{3}\gg\mid{y}−\mathrm{3}\mid \\ $$$$−\mathrm{3}\ll{y}−\mathrm{3}\ll\mathrm{3} \\ $$$$\mathrm{0}\ll{y}\ll\mathrm{6} \\ $$$$ \\ $$$$ \\ $$
Commented by 073 last updated on 10/Apr/23

$$\mathrm{nice}\:\mathrm{solution} \\ $$
Answered by mr W last updated on 10/Apr/23
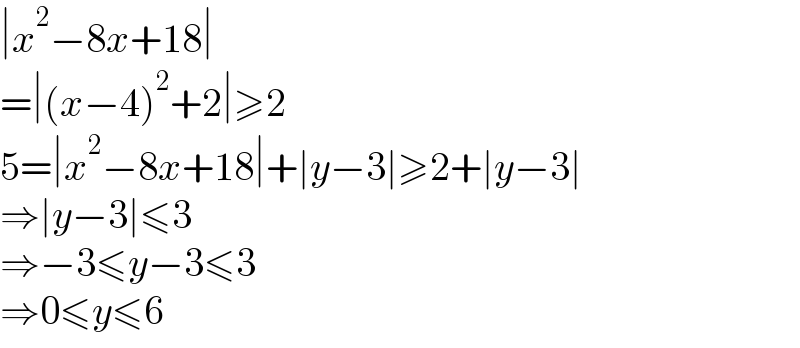
$$\mid{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{18}\mid \\ $$$$=\mid\left({x}−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{2}\mid\geqslant\mathrm{2} \\ $$$$\mathrm{5}=\mid{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{18}\mid+\mid{y}−\mathrm{3}\mid\geqslant\mathrm{2}+\mid{y}−\mathrm{3}\mid \\ $$$$\Rightarrow\mid{y}−\mathrm{3}\mid\leqslant\mathrm{3} \\ $$$$\Rightarrow−\mathrm{3}\leqslant{y}−\mathrm{3}\leqslant\mathrm{3} \\ $$$$\Rightarrow\mathrm{0}\leqslant{y}\leqslant\mathrm{6} \\ $$
Commented by manxsol last updated on 11/Apr/23
$${Win}\:\:{Sir}\:{W}.\:{Very}\:{simple} \\ $$$$\:{solution} \\ $$
