Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 62251 by hovea cw last updated on 18/Jun/19

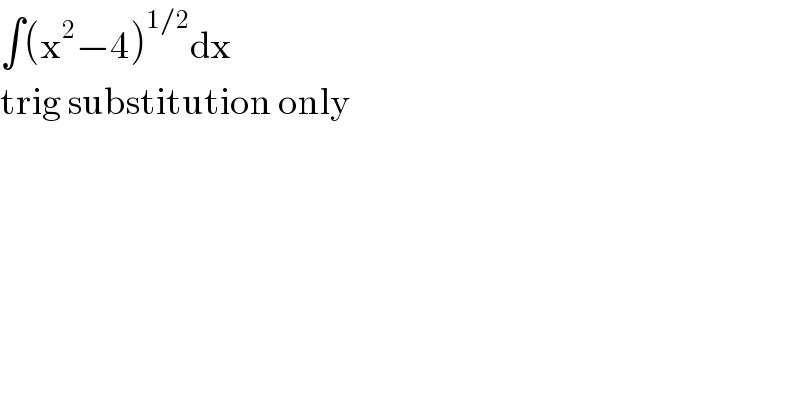
∫(x^2 −4)^(1/2) dx trig substitution only

$$\int\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{1}/\mathrm{2}} \mathrm{dx} \\ $$$$\mathrm{trig}\:\mathrm{substitution}\:\mathrm{only} \\ $$

Commented by maxmathsup by imad last updated on 18/Jun/19

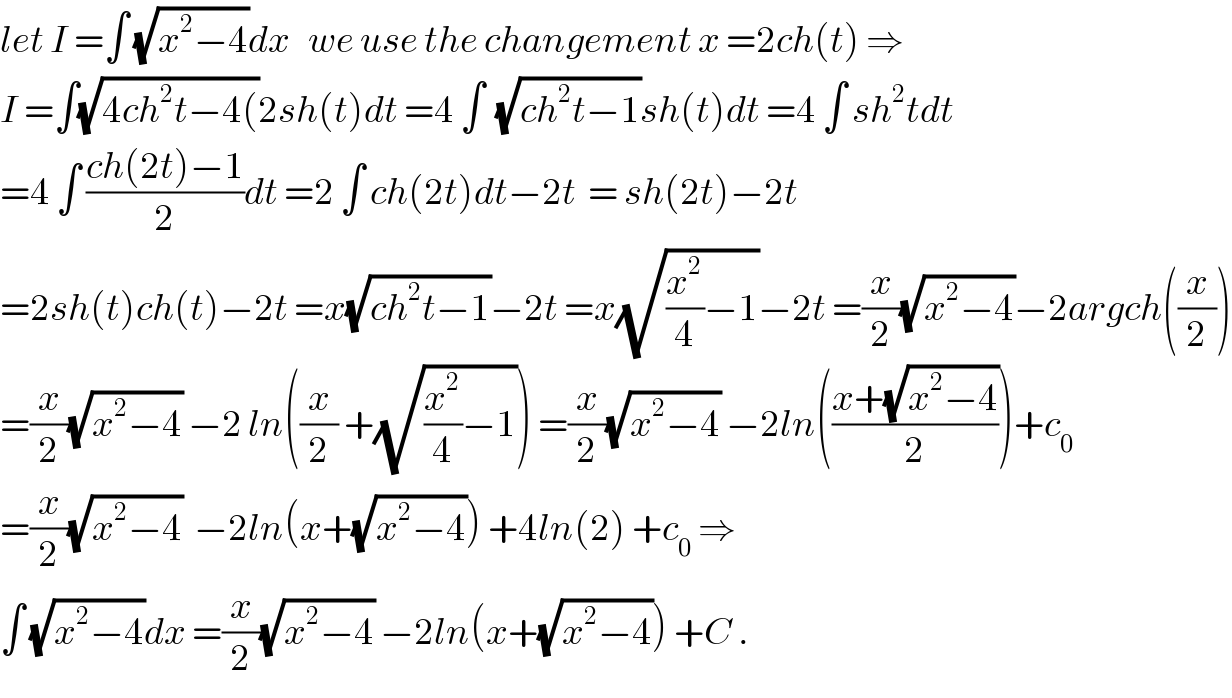
let I =∫ (√(x^2 −4))dx we use the changement x =2ch(t) ⇒ I =∫(√(4ch^2 t−4())2sh(t)dt =4 ∫ (√(ch^2 t−1))sh(t)dt =4 ∫ sh^2 tdt =4 ∫ ((ch(2t)−1)/2)dt =2 ∫ ch(2t)dt−2t = sh(2t)−2t =2sh(t)ch(t)−2t =x(√(ch^2 t−1))−2t =x(√((x^2 /4)−1))−2t =(x/2)(√(x^2 −4))−2argch((x/2)) =(x/2)(√(x^2 −4)) −2 ln((x/2) +(√((x^2 /4)−1))) =(x/2)(√(x^2 −4)) −2ln(((x+(√(x^2 −4)))/2))+c_0 =(x/2)(√(x^2 −4)) −2ln(x+(√(x^2 −4))) +4ln(2) +c_0 ⇒ ∫ (√(x^2 −4))dx =(x/2)(√(x^2 −4)) −2ln(x+(√(x^2 −4))) +C .

$${let}\:{I}\:=\int\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}{dx}\:\:\:{we}\:{use}\:{the}\:{changement}\:{x}\:=\mathrm{2}{ch}\left({t}\right)\:\Rightarrow \\ $$$${I}\:=\int\sqrt{\mathrm{4}{ch}^{\mathrm{2}} {t}−\mathrm{4}\left(\right.}\mathrm{2}{sh}\left({t}\right){dt}\:=\mathrm{4}\:\int\:\:\sqrt{{ch}^{\mathrm{2}} {t}−\mathrm{1}}{sh}\left({t}\right){dt}\:=\mathrm{4}\:\int\:{sh}^{\mathrm{2}} {tdt} \\ $$$$=\mathrm{4}\:\int\:\frac{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}}{\mathrm{2}}{dt}\:=\mathrm{2}\:\int\:{ch}\left(\mathrm{2}{t}\right){dt}−\mathrm{2}{t}\:\:=\:{sh}\left(\mathrm{2}{t}\right)−\mathrm{2}{t} \\ $$$$=\mathrm{2}{sh}\left({t}\right){ch}\left({t}\right)−\mathrm{2}{t}\:={x}\sqrt{{ch}^{\mathrm{2}} {t}−\mathrm{1}}−\mathrm{2}{t}\:={x}\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{1}}−\mathrm{2}{t}\:=\frac{{x}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}−\mathrm{2}{argch}\left(\frac{{x}}{\mathrm{2}}\right) \\ $$$$=\frac{{x}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}\:−\mathrm{2}\:{ln}\left(\frac{{x}}{\mathrm{2}}\:+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{1}}\right)\:=\frac{{x}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}\:−\mathrm{2}{ln}\left(\frac{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\right)+{c}_{\mathrm{0}} \\ $$$$=\frac{{x}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}\:\:−\mathrm{2}{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}\right)\:+\mathrm{4}{ln}\left(\mathrm{2}\right)\:+{c}_{\mathrm{0}} \:\Rightarrow \\ $$$$\int\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}{dx}\:=\frac{{x}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}\:−\mathrm{2}{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}\right)\:+{C}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com