
Question Number 121590 by pooooop last updated on 09/Nov/20

$$\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{{x}}=\mathrm{8}\sqrt{\mathrm{6}} \\ $$$$\mathrm{2}\boldsymbol{{x}}−\frac{\mathrm{12}}{\boldsymbol{{x}}}=? \\ $$
Answered by mathmax by abdo last updated on 09/Nov/20
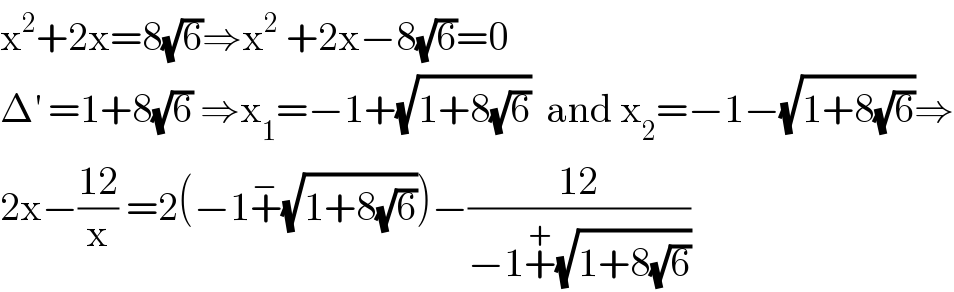
$$\mathrm{x}^{\mathrm{2}} +\mathrm{2x}=\mathrm{8}\sqrt{\mathrm{6}}\Rightarrow\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}−\mathrm{8}\sqrt{\mathrm{6}}=\mathrm{0} \\ $$$$\Delta^{'} \:=\mathrm{1}+\mathrm{8}\sqrt{\mathrm{6}}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =−\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{8}\sqrt{\mathrm{6}}}\:\:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =−\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{8}\sqrt{\mathrm{6}}}\Rightarrow \\ $$$$\mathrm{2x}−\frac{\mathrm{12}}{\mathrm{x}}\:=\mathrm{2}\left(−\mathrm{1}\overset{−} {+}\sqrt{\mathrm{1}+\mathrm{8}\sqrt{\mathrm{6}}}\right)−\frac{\mathrm{12}}{−\mathrm{1}\overset{+} {+}\sqrt{\mathrm{1}+\mathrm{8}\sqrt{\mathrm{6}}}} \\ $$
