Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 211675 by MrGaster last updated on 16/Sep/24

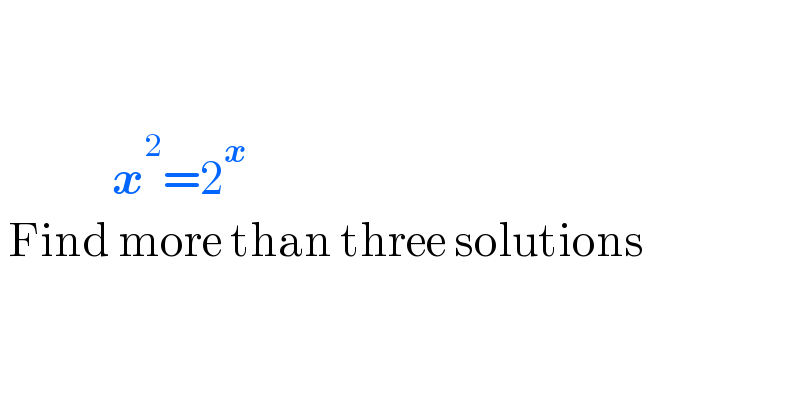
x^2 =2^x Find more than three solutions

$$ \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{x}}^{\mathrm{2}} =\mathrm{2}^{\boldsymbol{{x}}} \\ $$$$\:\mathrm{Find}\:\mathrm{more}\:\mathrm{than}\:\mathrm{three}\:\mathrm{solutions} \\ $$$$ \\ $$

Commented by mr W last updated on 16/Sep/24

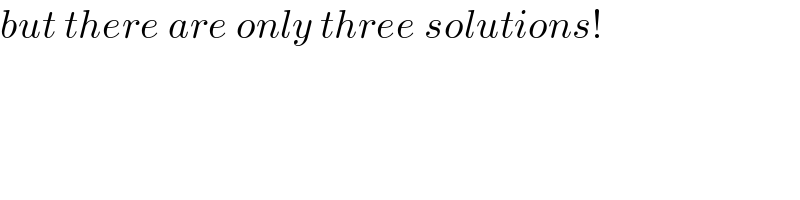
but there are only three solutions!

$${but}\:{there}\:{are}\:{only}\:{three}\:{solutions}! \\ $$

Answered by mr W last updated on 16/Sep/24

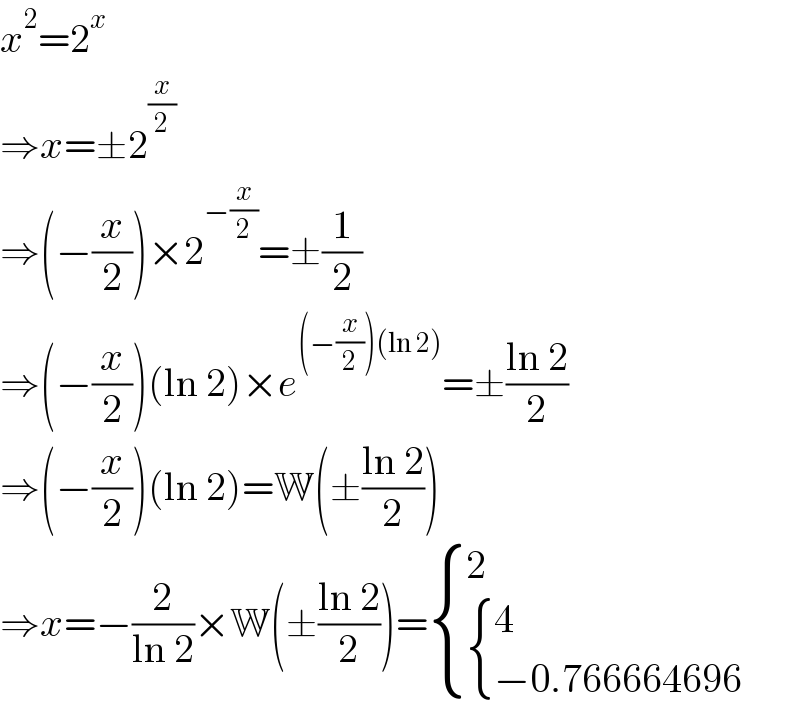
x^2 =2^x ⇒x=±2^(x/2) ⇒(−(x/2))×2^(−(x/2)) =±(1/2) ⇒(−(x/2))(ln 2)×e^((−(x/2))(ln 2)) =±((ln 2)/2) ⇒(−(x/2))(ln 2)=W(±((ln 2)/2)) ⇒x=−(2/(ln 2))×W(±((ln 2)/2))= { (2),( { (4),((−0.766664696)) :}) :}

$${x}^{\mathrm{2}} =\mathrm{2}^{{x}} \\ $$$$\Rightarrow{x}=\pm\mathrm{2}^{\frac{{x}}{\mathrm{2}}} \\ $$$$\Rightarrow\left(−\frac{{x}}{\mathrm{2}}\right)×\mathrm{2}^{−\frac{{x}}{\mathrm{2}}} =\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\left(−\frac{{x}}{\mathrm{2}}\right)\left(\mathrm{ln}\:\mathrm{2}\right)×{e}^{\left(−\frac{{x}}{\mathrm{2}}\right)\left(\mathrm{ln}\:\mathrm{2}\right)} =\pm\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}} \\ $$$$\Rightarrow\left(−\frac{{x}}{\mathrm{2}}\right)\left(\mathrm{ln}\:\mathrm{2}\right)=\mathbb{W}\left(\pm\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{x}=−\frac{\mathrm{2}}{\mathrm{ln}\:\mathrm{2}}×\mathbb{W}\left(\pm\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)=\begin{cases}{\mathrm{2}}\\{\begin{cases}{\mathrm{4}}\\{−\mathrm{0}.\mathrm{766664696}}\end{cases}}\end{cases} \\ $$

Answered by Frix last updated on 16/Sep/24

x^2 =2^x 2ln x =xln 2 −((ln x)/x)=−((ln 2)/2) x=e^(−t) e^t t+((ln 2)/2)=0 t=a+bi (e^a (acos b −bsin b)+((ln 2)/2))+e^a (asin b +bcos b)i=0 { ((e^a (acos b −bsin b)+((ln 2)/2)=0)),((e^a (asin b +bcos b)=0 ⇒ a=−bcot b)) :} ⇒ ((2b)/(sin b))−e^(bcot b) ln 2 =0 [approximate] t=−b(cot b −i) x=e^(bcot b) (cos b −i sin b) 2 solutions ∉R: b≈±7.45408757255 x≈9.09072986075±21.5079503505i

$${x}^{\mathrm{2}} =\mathrm{2}^{{x}} \\ $$$$\mathrm{2ln}\:{x}\:={x}\mathrm{ln}\:\mathrm{2} \\ $$$$−\frac{\mathrm{ln}\:{x}}{{x}}=−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}} \\ $$$${x}=\mathrm{e}^{−{t}} \\ $$$$\mathrm{e}^{{t}} {t}+\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}=\mathrm{0} \\ $$$${t}={a}+{b}\mathrm{i} \\ $$$$\left(\mathrm{e}^{{a}} \left({a}\mathrm{cos}\:{b}\:−{b}\mathrm{sin}\:{b}\right)+\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)+\mathrm{e}^{{a}} \left({a}\mathrm{sin}\:{b}\:+{b}\mathrm{cos}\:{b}\right)\mathrm{i}=\mathrm{0} \\ $$$$\begin{cases}{\mathrm{e}^{{a}} \left({a}\mathrm{cos}\:{b}\:−{b}\mathrm{sin}\:{b}\right)+\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}=\mathrm{0}}\\{\mathrm{e}^{{a}} \left({a}\mathrm{sin}\:{b}\:+{b}\mathrm{cos}\:{b}\right)=\mathrm{0}\:\Rightarrow\:{a}=−{b}\mathrm{cot}\:{b}}\end{cases} \\ $$$$\Rightarrow \\ $$$$\frac{\mathrm{2}{b}}{\mathrm{sin}\:{b}}−\mathrm{e}^{{b}\mathrm{cot}\:{b}} \:\mathrm{ln}\:\mathrm{2}\:=\mathrm{0}\:\left[\mathrm{approximate}\right] \\ $$$${t}=−{b}\left(\mathrm{cot}\:{b}\:−\mathrm{i}\right) \\ $$$${x}=\mathrm{e}^{{b}\mathrm{cot}\:{b}} \left(\mathrm{cos}\:{b}\:−\mathrm{i}\:\mathrm{sin}\:{b}\right) \\ $$$$ \\ $$$$\mathrm{2}\:\mathrm{solutions}\:\notin\mathbb{R}: \\ $$$${b}\approx\pm\mathrm{7}.\mathrm{45408757255} \\ $$$${x}\approx\mathrm{9}.\mathrm{09072986075}\pm\mathrm{21}.\mathrm{5079503505i} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com