Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 193182 by York12 last updated on 06/Jun/23

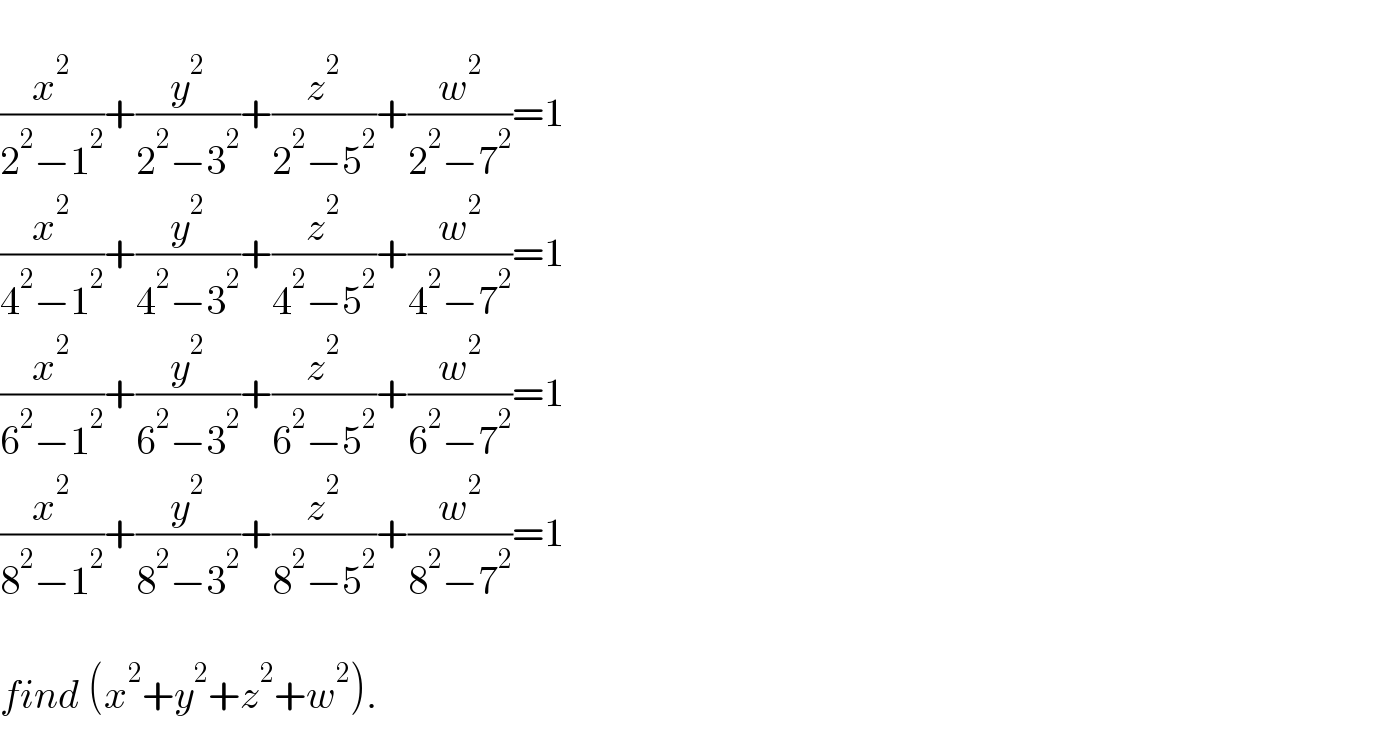
(x^2 /(2^2 −1^2 ))+(y^2 /(2^2 −3^2 ))+(z^2 /(2^2 −5^2 ))+(w^2 /(2^2 −7^2 ))=1 (x^2 /(4^2 −1^2 ))+(y^2 /(4^2 −3^2 ))+(z^2 /(4^2 −5^2 ))+(w^2 /(4^2 −7^2 ))=1 (x^2 /(6^2 −1^2 ))+(y^2 /(6^2 −3^2 ))+(z^2 /(6^2 −5^2 ))+(w^2 /(6^2 −7^2 ))=1 (x^2 /(8^2 −1^2 ))+(y^2 /(8^2 −3^2 ))+(z^2 /(8^2 −5^2 ))+(w^2 /(8^2 −7^2 ))=1 find (x^2 +y^2 +z^2 +w^2 ).

$$ \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }+\frac{{z}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }+\frac{{w}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{4}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{\mathrm{4}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }+\frac{{z}^{\mathrm{2}} }{\mathrm{4}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }+\frac{{w}^{\mathrm{2}} }{\mathrm{4}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{6}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{\mathrm{6}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }+\frac{{z}^{\mathrm{2}} }{\mathrm{6}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }+\frac{{w}^{\mathrm{2}} }{\mathrm{6}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{8}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{\mathrm{8}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }+\frac{{z}^{\mathrm{2}} }{\mathrm{8}^{\mathrm{2}} −\mathrm{5}^{\mathrm{2}} }+\frac{{w}^{\mathrm{2}} }{\mathrm{8}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} }=\mathrm{1}\: \\ $$$$ \\ $$$${find}\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} +{w}^{\mathrm{2}} \right). \\ $$

Answered by York12 last updated on 06/Jun/23

Let s takes the values (4 , 16 , 36 , 64) ∴ (x^2 /(s−1))+(y^2 /(s−9))+(z^2 /(s−25))+(w^2 /(s−49))=1 ⇒ x^2 (s−9)(s−25)(s−49) + y^2 (s−1)(s−25)(s−49)+z^2 (s−1)(s−9)(s−49)+w^2 (s−1)(s−9)(s−25)=(s−1)(s−9)(s−25)(s−49) ⇒x^2 (s−9)(s−25)(s−49) + y^2 (s−1)(s−25)(s−49)+z^2 (s−1)(s−9)(s−49)+w^2 (s−1)(s−9)(s−25)−(s−1)(s−9)(s−25)(s−49)=0 let the previous expression be a quartic polynomial in s with leading coefficient of (−1) and we know the values of s for which that holds s ∈ { 4 , 16 , 36 , 64 } Then : x^2 (s−9)(s−25)(s−49) + y^2 (s−1)(s−25)(s−49)+z^2 (s−1)(s−9)(s−49)+w^2 (s−1)(s−9)(s−25)−(s−1)(s−9)(s−25)(s−49)= −(s−4)(s−16)(s−36)(s−64) = f(s) f(1)= −(3×15×35×63)=−x^2 (8×24×48) ⇒x^2 =((3×15×35×63)/(8×24×48)) .......(i) f(9)=(5×7×27×55)=y^2 (8×16×40) ⇒ y^2 =(((5×7×27×55))/((8×16×40))) .......(ii) f(25)=−(21×9×11×39)=−z^2 (24×16×24) ⇒ z^2 =(((21×9×11×39))/((24×16×24)))......(iii) f(49)=(45×33×13×15)=w^2 (48×40×24) ⇒w^2 =(((45×33×13×15))/((48×40×24))) .......(iv) (i)+(ii)+(iii)+(iv)= 36 ★

$$ \\ $$$$\boldsymbol{{Let}}\:\boldsymbol{{s}}\:\boldsymbol{{takes}}\:\boldsymbol{{the}}\:\boldsymbol{{values}}\:\left(\mathrm{4}\:,\:\mathrm{16}\:,\:\mathrm{36}\:,\:\mathrm{64}\right) \\ $$$$\therefore\:\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\boldsymbol{{s}}−\mathrm{1}}+\frac{\boldsymbol{{y}}^{\mathrm{2}} }{\boldsymbol{{s}}−\mathrm{9}}+\frac{\boldsymbol{{z}}^{\mathrm{2}} }{\boldsymbol{{s}}−\mathrm{25}}+\frac{\boldsymbol{{w}}^{\mathrm{2}} }{\boldsymbol{{s}}−\mathrm{49}}=\mathrm{1} \\ $$$$\Rightarrow\:\boldsymbol{{x}}^{\mathrm{2}} \left(\boldsymbol{{s}}−\mathrm{9}\right)\left(\boldsymbol{{s}}−\mathrm{25}\right)\left(\boldsymbol{{s}}−\mathrm{49}\right)\:+\:\boldsymbol{{y}}^{\mathrm{2}} \left(\boldsymbol{{s}}−\mathrm{1}\right)\left(\boldsymbol{{s}}−\mathrm{25}\right)\left(\boldsymbol{{s}}−\mathrm{49}\right)+\boldsymbol{{z}}^{\mathrm{2}} \left(\boldsymbol{{s}}−\mathrm{1}\right)\left(\boldsymbol{{s}}−\mathrm{9}\right)\left(\boldsymbol{{s}}−\mathrm{49}\right)+\boldsymbol{{w}}^{\mathrm{2}} \left(\boldsymbol{{s}}−\mathrm{1}\right)\left(\boldsymbol{{s}}−\mathrm{9}\right)\left(\boldsymbol{{s}}−\mathrm{25}\right)=\left(\boldsymbol{{s}}−\mathrm{1}\right)\left(\boldsymbol{{s}}−\mathrm{9}\right)\left(\boldsymbol{{s}}−\mathrm{25}\right)\left(\boldsymbol{{s}}−\mathrm{49}\right) \\ $$$$\Rightarrow\boldsymbol{{x}}^{\mathrm{2}} \left(\boldsymbol{{s}}−\mathrm{9}\right)\left(\boldsymbol{{s}}−\mathrm{25}\right)\left(\boldsymbol{{s}}−\mathrm{49}\right)\:+\:\boldsymbol{{y}}^{\mathrm{2}} \left(\boldsymbol{{s}}−\mathrm{1}\right)\left(\boldsymbol{{s}}−\mathrm{25}\right)\left(\boldsymbol{{s}}−\mathrm{49}\right)+\boldsymbol{{z}}^{\mathrm{2}} \left(\boldsymbol{{s}}−\mathrm{1}\right)\left(\boldsymbol{{s}}−\mathrm{9}\right)\left(\boldsymbol{{s}}−\mathrm{49}\right)+\boldsymbol{{w}}^{\mathrm{2}} \left(\boldsymbol{{s}}−\mathrm{1}\right)\left(\boldsymbol{{s}}−\mathrm{9}\right)\left(\boldsymbol{{s}}−\mathrm{25}\right)−\left(\boldsymbol{{s}}−\mathrm{1}\right)\left(\boldsymbol{{s}}−\mathrm{9}\right)\left(\boldsymbol{{s}}−\mathrm{25}\right)\left(\boldsymbol{{s}}−\mathrm{49}\right)=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{let}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{previous}}\:\boldsymbol{\mathrm{expression}}\:\boldsymbol{\mathrm{be}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{quartic}} \\ $$$$\boldsymbol{{polynomial}}\:\boldsymbol{{in}}\:\boldsymbol{{s}}\:\boldsymbol{{with}}\:\boldsymbol{{leading}}\:\boldsymbol{{coefficient}}\:\boldsymbol{{of}}\:\left(−\mathrm{1}\right) \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{we}}\:\boldsymbol{{know}}\:\boldsymbol{{the}}\:\boldsymbol{{values}}\:\boldsymbol{{of}}\:\boldsymbol{{s}}\:\boldsymbol{{for}}\:\boldsymbol{{which}}\:\boldsymbol{{that}} \\ $$$$\boldsymbol{{holds}}\:\boldsymbol{{s}}\:\in\:\left\{\:\mathrm{4}\:,\:\mathrm{16}\:,\:\mathrm{36}\:,\:\mathrm{64}\:\right\}\: \\ $$$$\:\boldsymbol{{Then}}\::\: \\ $$$$\boldsymbol{{x}}^{\mathrm{2}} \left(\boldsymbol{{s}}−\mathrm{9}\right)\left(\boldsymbol{{s}}−\mathrm{25}\right)\left(\boldsymbol{{s}}−\mathrm{49}\right)\:+\:\boldsymbol{{y}}^{\mathrm{2}} \left(\boldsymbol{{s}}−\mathrm{1}\right)\left(\boldsymbol{{s}}−\mathrm{25}\right)\left(\boldsymbol{{s}}−\mathrm{49}\right)+\boldsymbol{{z}}^{\mathrm{2}} \left(\boldsymbol{{s}}−\mathrm{1}\right)\left(\boldsymbol{{s}}−\mathrm{9}\right)\left(\boldsymbol{{s}}−\mathrm{49}\right)+\boldsymbol{{w}}^{\mathrm{2}} \left(\boldsymbol{{s}}−\mathrm{1}\right)\left(\boldsymbol{{s}}−\mathrm{9}\right)\left(\boldsymbol{{s}}−\mathrm{25}\right)−\left(\boldsymbol{{s}}−\mathrm{1}\right)\left(\boldsymbol{{s}}−\mathrm{9}\right)\left(\boldsymbol{{s}}−\mathrm{25}\right)\left(\boldsymbol{{s}}−\mathrm{49}\right)= \\ $$$$−\left(\boldsymbol{{s}}−\mathrm{4}\right)\left(\boldsymbol{{s}}−\mathrm{16}\right)\left(\boldsymbol{{s}}−\mathrm{36}\right)\left(\boldsymbol{{s}}−\mathrm{64}\right)\:=\:\boldsymbol{{f}}\left(\boldsymbol{{s}}\right) \\ $$$$\boldsymbol{{f}}\left(\mathrm{1}\right)=\:−\left(\mathrm{3}×\mathrm{15}×\mathrm{35}×\mathrm{63}\right)=−\boldsymbol{{x}}^{\mathrm{2}} \left(\mathrm{8}×\mathrm{24}×\mathrm{48}\right) \\ $$$$\Rightarrow\boldsymbol{{x}}^{\mathrm{2}} =\frac{\mathrm{3}×\mathrm{15}×\mathrm{35}×\mathrm{63}}{\mathrm{8}×\mathrm{24}×\mathrm{48}}\:.......\left(\boldsymbol{{i}}\right) \\ $$$$\boldsymbol{{f}}\left(\mathrm{9}\right)=\left(\mathrm{5}×\mathrm{7}×\mathrm{27}×\mathrm{55}\right)=\boldsymbol{{y}}^{\mathrm{2}} \left(\mathrm{8}×\mathrm{16}×\mathrm{40}\right)\: \\ $$$$\Rightarrow\:\boldsymbol{{y}}^{\mathrm{2}} =\frac{\left(\mathrm{5}×\mathrm{7}×\mathrm{27}×\mathrm{55}\right)}{\left(\mathrm{8}×\mathrm{16}×\mathrm{40}\right)}\:.......\left(\boldsymbol{{ii}}\right) \\ $$$$\boldsymbol{{f}}\left(\mathrm{25}\right)=−\left(\mathrm{21}×\mathrm{9}×\mathrm{11}×\mathrm{39}\right)=−\boldsymbol{{z}}^{\mathrm{2}} \left(\mathrm{24}×\mathrm{16}×\mathrm{24}\right) \\ $$$$\Rightarrow\:\boldsymbol{{z}}^{\mathrm{2}} =\frac{\left(\mathrm{21}×\mathrm{9}×\mathrm{11}×\mathrm{39}\right)}{\left(\mathrm{24}×\mathrm{16}×\mathrm{24}\right)}......\left(\boldsymbol{{iii}}\right) \\ $$$$\boldsymbol{{f}}\left(\mathrm{49}\right)=\left(\mathrm{45}×\mathrm{33}×\mathrm{13}×\mathrm{15}\right)=\boldsymbol{{w}}^{\mathrm{2}} \left(\mathrm{48}×\mathrm{40}×\mathrm{24}\right) \\ $$$$\Rightarrow\boldsymbol{{w}}^{\mathrm{2}} =\frac{\left(\mathrm{45}×\mathrm{33}×\mathrm{13}×\mathrm{15}\right)}{\left(\mathrm{48}×\mathrm{40}×\mathrm{24}\right)}\:.......\left(\boldsymbol{{iv}}\right) \\ $$$$\left(\boldsymbol{{i}}\right)+\left(\boldsymbol{{ii}}\right)+\left(\boldsymbol{{iii}}\right)+\left(\boldsymbol{{iv}}\right)=\:\mathrm{36}\:\bigstar \\ $$

Commented by manxsol last updated on 06/Jun/23

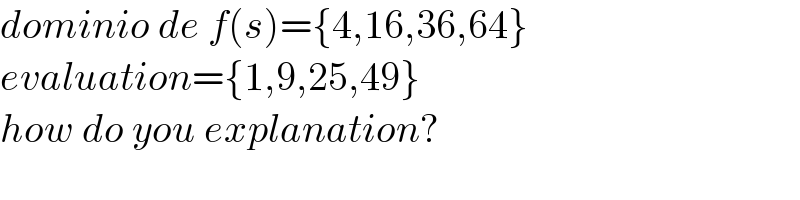
dominio de f(s)={4,16,36,64} evaluation={1,9,25,49} how do you explanation?

$${dominio}\:{de}\:{f}\left({s}\right)=\left\{\mathrm{4},\mathrm{16},\mathrm{36},\mathrm{64}\right\} \\ $$$${evaluation}=\left\{\mathrm{1},\mathrm{9},\mathrm{25},\mathrm{49}\right\}\: \\ $$$${how}\:{do}\:{you}\:{explanation}? \\ $$

Commented by York12 last updated on 07/Jun/23

{4,16,36,64} that is the solution set for which f(s)=0 {1,9,25,49} those are just values I have plugged them into the function to eliminate x^2 , y^2 , z^2 , w^2 so that I can obtain their values

$$\left\{\mathrm{4},\mathrm{16},\mathrm{36},\mathrm{64}\right\}\:{that}\:{is}\:{the}\:{solution}\:{set}\: \\ $$$${for}\:{which}\:{f}\left({s}\right)=\mathrm{0} \\ $$$$\left\{\mathrm{1},\mathrm{9},\mathrm{25},\mathrm{49}\right\}\:{those}\:{are}\:{just}\:{values}\:{I}\:{have}\: \\ $$$${plugged}\:{them}\:{into}\:{the}\:{function}\:{to}\: \\ $$$${eliminate}\:{x}^{\mathrm{2}} \:,\:{y}^{\mathrm{2}} \:,\:{z}^{\mathrm{2}} \:,\:{w}^{\mathrm{2}} \\ $$$${so}\:{that}\:{I}\:{can}\:{obtain}\:{their}\:{values} \\ $$$$ \\ $$$$ \\ $$

Commented by manxsol last updated on 07/Jun/23

thank for explanation.

$${thank}\:{for}\:{explanation}. \\ $$

Commented by York12 last updated on 07/Jun/23

you are welcome

$${you}\:{are}\:{welcome} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com