
Question Number 211152 by Spillover last updated on 29/Aug/24
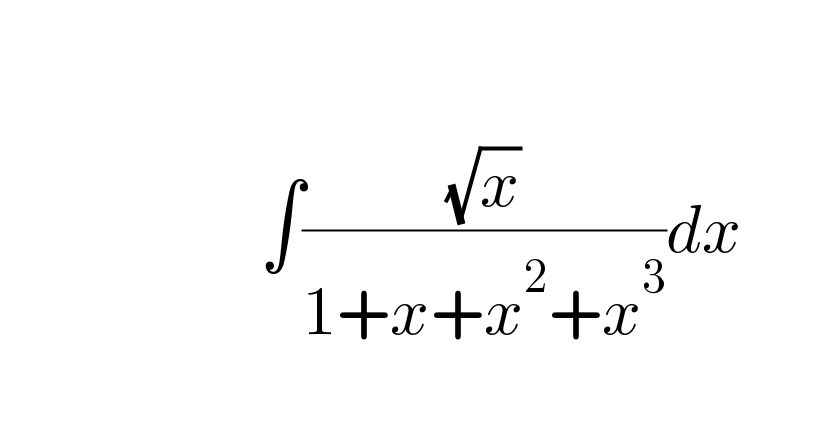
$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int\frac{\sqrt{{x}}}{\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }{dx} \\ $$$$ \\ $$
Answered by Ghisom last updated on 22/Sep/24
![∫((√x)/(1+x+x^2 +x^3 ))dx= [t=((√(2x))/(x−1))] =−((√2)/2)∫(t^2 /((t^2 +1)(2t^2 +1)))dt= =((√2)/2)∫((1/(2t^2 +1))−(1/(t^2 +1)))dt= =(1/2)arctan (√2)t −((√2)/2)arctan t = =(1/2)arctan ((2(√x))/(x−1)) −((√2)/2)arctan ((√(2x))/(x−1)) +C](Q211833.png)
$$\int\frac{\sqrt{{x}}}{\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{\mathrm{2}{x}}}{{x}−\mathrm{1}}\right] \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}\right)}{dt}= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}\right){dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\:\sqrt{\mathrm{2}}{t}\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{arctan}\:{t}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\:\frac{\mathrm{2}\sqrt{{x}}}{{x}−\mathrm{1}}\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{2}{x}}}{{x}−\mathrm{1}}\:+{C} \\ $$
