
Question Number 191451 by mathlove last updated on 24/Apr/23
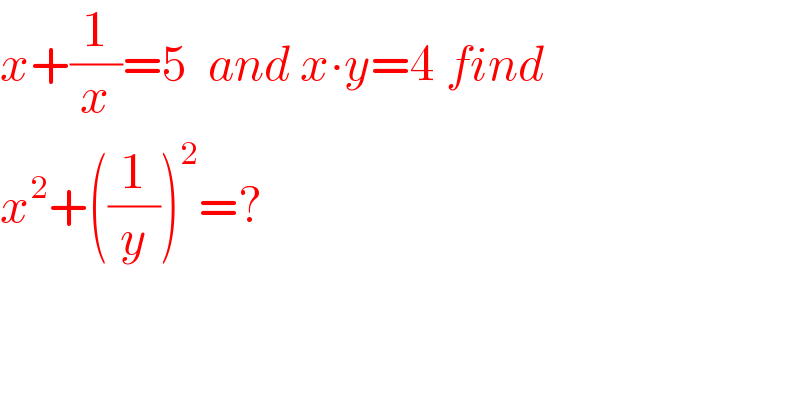
$${x}+\frac{\mathrm{1}}{{x}}=\mathrm{5}\:\:{and}\:{x}\centerdot{y}=\mathrm{4}\:{find} \\ $$$${x}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} =? \\ $$
Answered by mr W last updated on 24/Apr/23
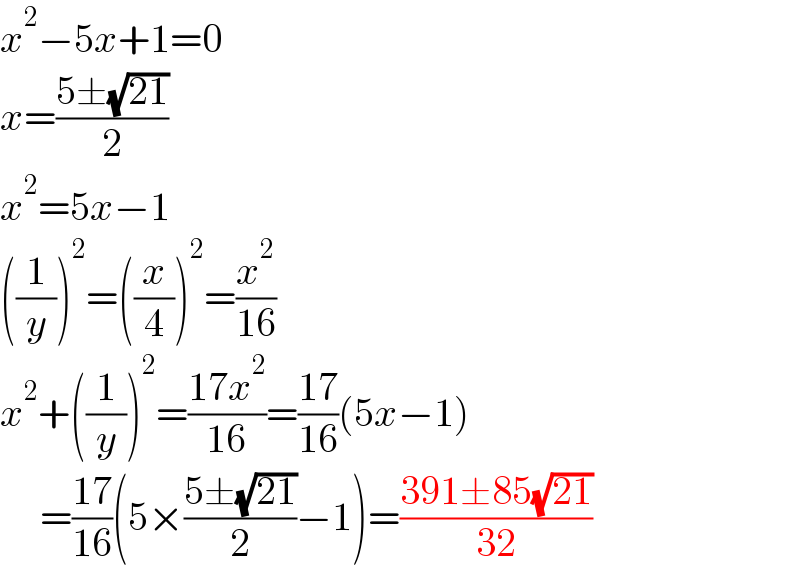
$${x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{5}\pm\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} =\mathrm{5}{x}−\mathrm{1} \\ $$$$\left(\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} =\left(\frac{{x}}{\mathrm{4}}\right)^{\mathrm{2}} =\frac{{x}^{\mathrm{2}} }{\mathrm{16}} \\ $$$${x}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} =\frac{\mathrm{17}{x}^{\mathrm{2}} }{\mathrm{16}}=\frac{\mathrm{17}}{\mathrm{16}}\left(\mathrm{5}{x}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:=\frac{\mathrm{17}}{\mathrm{16}}\left(\mathrm{5}×\frac{\mathrm{5}\pm\sqrt{\mathrm{21}}}{\mathrm{2}}−\mathrm{1}\right)=\frac{\mathrm{391}\pm\mathrm{85}\sqrt{\mathrm{21}}}{\mathrm{32}} \\ $$
Commented by mehdee42 last updated on 24/Apr/23

$${sir}\:{W} \\ $$$${please}\:{guide}\:{me}\:{how}\:{can}\:{i}\:{submit}\:\:{a}\:{question}\:{in}\:{the}\:{group}? \\ $$
Commented by Tinku Tara last updated on 24/Apr/23
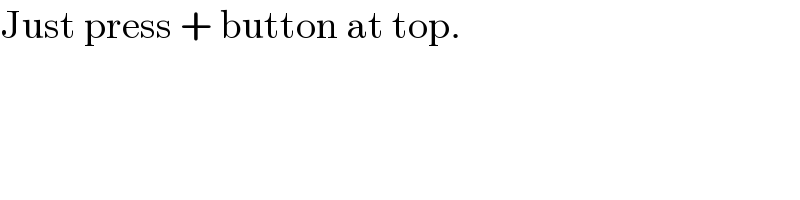
$$\mathrm{Just}\:\mathrm{press}\:+\:\mathrm{button}\:\mathrm{at}\:\mathrm{top}. \\ $$
Commented by mr W last updated on 24/Apr/23

$${to}\:{compose}\:{a}\:{new}\:{question}\:{just}\:{press} \\ $$$$``+''\:{button}\:{at}\:{the}\:{top}; \\ $$$${to}\:{post}\:{an}\:{image}\:{as}\:{a}\:{question}\:{just} \\ $$$${press}\:``{image}''\:{button}\:{at}\:{the}\:{top}. \\ $$
Commented by mr W last updated on 24/Apr/23
Commented by mehdee42 last updated on 24/Apr/23
$${thank}\:{you}\:{very}\:{much}\:{for}\:{your}\:{kidness} \\ $$
Commented by mathlove last updated on 25/Apr/23

$${thanks} \\ $$
