
Question Number 123920 by john_santu last updated on 29/Nov/20
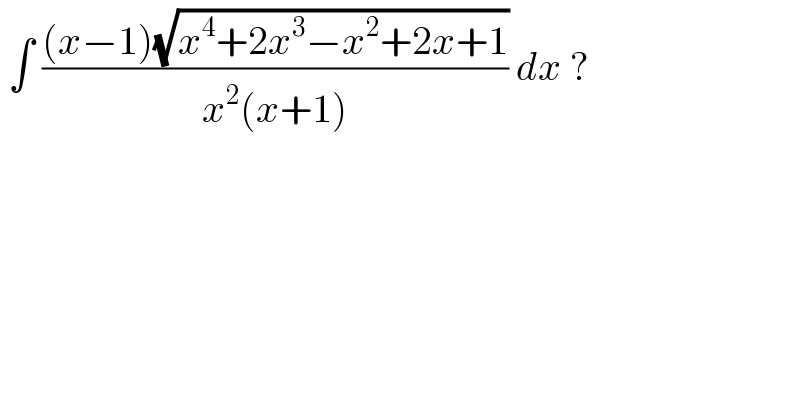
$$\:\int\:\frac{\left({x}−\mathrm{1}\right)\sqrt{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}\:{dx}\:? \\ $$
Answered by liberty last updated on 29/Nov/20
![(•) ((x−1)/(x^2 (x+1))) = ((x^2 −1)/(x^2 (x+1)^2 )) =(1−(1/x^2 ))((1/(x^2 (x+(1/x)+2)))) (••) x^4 +2x^3 −x^2 +2x+1=x^2 (x^2 +(1/x^2 )+2(x+(1/x))−1) = x^2 ((x+(1/x))^2 +2(x+(1/x))−3)=x^2 ((x+(1/x)+1)^2 −4) letting 2sec v = x+(1/x)+1 T=∫ ((√(4sec^2 v−4))/(2sec v+1)) (2sec v tan v )dv T=∫ ((4tan^2 v sec v )/(2sec v +1)) dv = ∫(2sec^2 v−sec v)dv−∫((3sec v dv)/(2sec v +1)) T= 2tan v −ℓn ∣sec v + tan v∣ −∫ ((3(2−cos v))/(4−cos^2 v)) dv let L=∫ ((6−3cos v)/(4−cos^2 v)) dv = ∫ ((6sec^2 v)/(4sec^2 v−1))dv−∫((3cos v)/(3+sin^2 v)) dv L=∫ ((6du)/(4u^2 +3)) [ u = tan v ] −∫((3dj)/(3+j^2 )) [ j = sin v ] L= (√3) tan^(−1) (((2u)/( (√3))))−(√3) tan^(−1) ((j/( (√3)))) L= (√3) tan^(−1) (((2tan v)/( (√3))))−(√3) tan^(−1) (((sin v)/( (√3)))) Thus T = 2tan v −ℓn∣sec v + tan v ∣− (√3) {tan^(−1) (((2tan v)/( (√3))))−tan^(−1) (((sin v)/( (√3))))}+ c where v = sec^(−1) (((x^2 +x+1)/(2x))) .](Q123923.png)
$$\left(\bullet\right)\:\frac{{x}−\mathrm{1}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}\:=\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:=\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left({x}+\frac{\mathrm{1}}{{x}}+\mathrm{2}\right)}\right) \\ $$$$\left(\bullet\bullet\right)\:{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}={x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{2}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{1}\right) \\ $$$$\:\:\:=\:{x}^{\mathrm{2}} \left(\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{3}\right)={x}^{\mathrm{2}} \left(\left({x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\right) \\ $$$${letting}\:\mathrm{2sec}\:{v}\:=\:{x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}\: \\ $$$${T}=\int\:\frac{\sqrt{\mathrm{4sec}\:^{\mathrm{2}} {v}−\mathrm{4}}}{\mathrm{2sec}\:{v}+\mathrm{1}}\:\left(\mathrm{2sec}\:{v}\:\mathrm{tan}\:{v}\:\right){dv} \\ $$$${T}=\int\:\frac{\mathrm{4tan}\:^{\mathrm{2}} {v}\:\mathrm{sec}\:{v}\:}{\mathrm{2sec}\:{v}\:+\mathrm{1}}\:{dv}\:=\:\int\left(\mathrm{2sec}\:^{\mathrm{2}} {v}−\mathrm{sec}\:{v}\right){dv}−\int\frac{\mathrm{3sec}\:{v}\:{dv}}{\mathrm{2sec}\:{v}\:+\mathrm{1}} \\ $$$${T}=\:\mathrm{2tan}\:{v}\:−\ell{n}\:\mid\mathrm{sec}\:{v}\:+\:\mathrm{tan}\:{v}\mid\:−\int\:\frac{\mathrm{3}\left(\mathrm{2}−\mathrm{cos}\:{v}\right)}{\mathrm{4}−\mathrm{cos}\:^{\mathrm{2}} {v}}\:{dv} \\ $$$${let}\:{L}=\int\:\frac{\mathrm{6}−\mathrm{3cos}\:{v}}{\mathrm{4}−\mathrm{cos}\:^{\mathrm{2}} {v}}\:{dv}\:=\:\int\:\frac{\mathrm{6sec}\:^{\mathrm{2}} {v}}{\mathrm{4sec}\:^{\mathrm{2}} {v}−\mathrm{1}}{dv}−\int\frac{\mathrm{3cos}\:{v}}{\mathrm{3}+\mathrm{sin}\:^{\mathrm{2}} {v}}\:{dv} \\ $$$${L}=\int\:\frac{\mathrm{6}{du}}{\mathrm{4}{u}^{\mathrm{2}} +\mathrm{3}}\:\left[\:{u}\:=\:\mathrm{tan}\:{v}\:\right]\:−\int\frac{\mathrm{3}{dj}}{\mathrm{3}+{j}^{\mathrm{2}} }\:\left[\:{j}\:=\:\mathrm{sin}\:{v}\:\right] \\ $$$${L}=\:\sqrt{\mathrm{3}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{u}}{\:\sqrt{\mathrm{3}}}\right)−\sqrt{\mathrm{3}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}}{\:\sqrt{\mathrm{3}}}\right)\: \\ $$$${L}=\:\sqrt{\mathrm{3}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2tan}\:{v}}{\:\sqrt{\mathrm{3}}}\right)−\sqrt{\mathrm{3}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:{v}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$${Thus}\:{T}\:=\:\mathrm{2tan}\:{v}\:−\ell{n}\mid\mathrm{sec}\:{v}\:+\:\mathrm{tan}\:{v}\:\mid− \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{\mathrm{3}}\:\left\{\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2tan}\:{v}}{\:\sqrt{\mathrm{3}}}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:{v}}{\:\sqrt{\mathrm{3}}}\right)\right\}+\:{c} \\ $$$${where}\:{v}\:=\:\mathrm{sec}^{−\mathrm{1}} \left(\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{\mathrm{2}{x}}\right)\:. \\ $$
Answered by MJS_new last updated on 29/Nov/20
![∫(((x−1)(√(x^4 +2x^3 −x^2 +2x+1)))/(x^2 (x+1)))dx= =∫(((x−1)(√((x^2 −x+1)(x^2 +3x+1))))/(x^2 (x+1)))dx= [t=((√(x^2 −x+1))/( (√(x^2 +3x+1)))) → dx=(((x^2 +3x+1)^(3/2) (√(x^2 −x+1)))/(2(x^2 −1)))dt] =32∫(t^2 /(t^6 +t^4 −5t^2 +3))dt= =32∫(t^2 /((t−1)^2 (t+1)^2 (t^2 +3)))dt= =2∫(dt/((t−1)^2 ))+2∫(dt/((t+1)^2 ))−6∫(dt/(t^2 +3))+∫(dt/(t−1))−∫(dt/(t+1))= =−(2/(t−1))−(2/(t+1))−2(√3)arctan (((√3)t)/3) +ln (t−1) −ln (t+1) = =−((4t)/(t^2 −1))−2(√3)arctan (((√3)t)/3) +ln ((t−1)/(t+1)) = =((√((x^2 −x+1)(x^2 +3x+1)))/x)−2(√3)arctan ((√(3(x^2 −x+1)))/(3(√(x^2 +3x+1)))) +ln ∣((x^2 +x+1−(√((x^2 −x+1)(x^2 +3x+1))))/(2x))∣ +C](Q123935.png)
$$\int\frac{\left({x}−\mathrm{1}\right)\sqrt{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}{dx}= \\ $$$$=\int\frac{\left({x}−\mathrm{1}\right)\sqrt{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right)}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}}}\:\rightarrow\:{dx}=\frac{\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} \sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{1}\right)}{dt}\right] \\ $$$$=\mathrm{32}\int\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{6}} +{t}^{\mathrm{4}} −\mathrm{5}{t}^{\mathrm{2}} +\mathrm{3}}{dt}= \\ $$$$=\mathrm{32}\int\frac{{t}^{\mathrm{2}} }{\left({t}−\mathrm{1}\right)^{\mathrm{2}} \left({t}+\mathrm{1}\right)^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{3}\right)}{dt}= \\ $$$$=\mathrm{2}\int\frac{{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }+\mathrm{2}\int\frac{{dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{6}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{3}}+\int\frac{{dt}}{{t}−\mathrm{1}}−\int\frac{{dt}}{{t}+\mathrm{1}}= \\ $$$$=−\frac{\mathrm{2}}{{t}−\mathrm{1}}−\frac{\mathrm{2}}{{t}+\mathrm{1}}−\mathrm{2}\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}{t}}{\mathrm{3}}\:+\mathrm{ln}\:\left({t}−\mathrm{1}\right)\:−\mathrm{ln}\:\left({t}+\mathrm{1}\right)\:= \\ $$$$=−\frac{\mathrm{4}{t}}{{t}^{\mathrm{2}} −\mathrm{1}}−\mathrm{2}\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}{t}}{\mathrm{3}}\:+\mathrm{ln}\:\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\:= \\ $$$$=\frac{\sqrt{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right)}}{{x}}−\mathrm{2}\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}}{\mathrm{3}\sqrt{{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}}}\:+\mathrm{ln}\:\mid\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}−\sqrt{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right)}}{\mathrm{2}{x}}\mid\:+{C} \\ $$
Commented by liberty last updated on 29/Nov/20

$${waw}\:{great} \\ $$
