Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 218103 by ArshadS last updated on 29/Mar/25

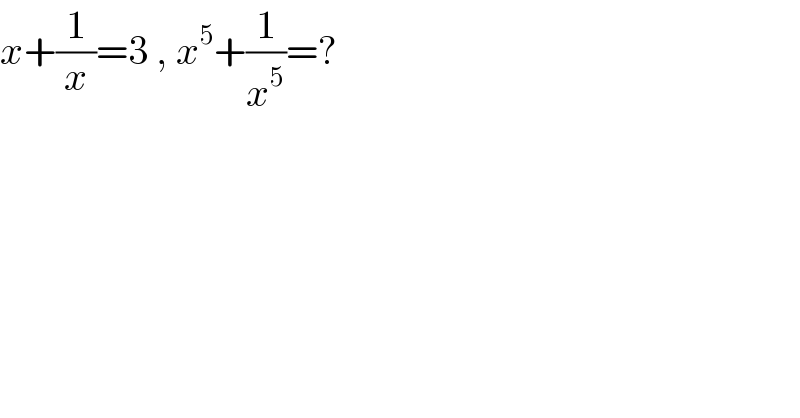
x+(1/x)=3 , x^5 +(1/x^5 )=?

$${x}+\frac{\mathrm{1}}{{x}}=\mathrm{3}\:,\:{x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }=? \\ $$

Answered by Rasheed.Sindhi last updated on 29/Mar/25

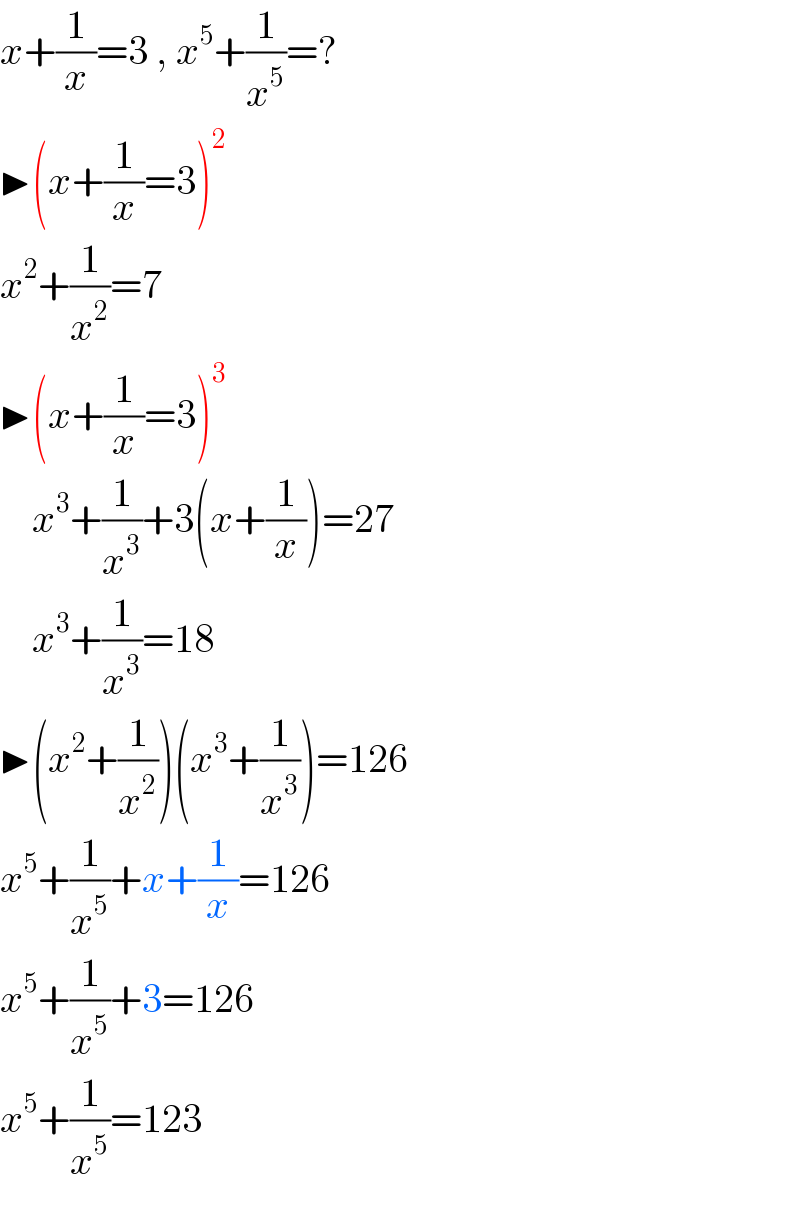
x+(1/x)=3 , x^5 +(1/x^5 )=? ▶(x+(1/x)=3)^2 x^2 +(1/x^2 )=7 ▶(x+(1/x)=3)^3 x^3 +(1/x^3 )+3(x+(1/x))=27 x^3 +(1/x^3 )=18 ▶(x^2 +(1/x^2 ))(x^3 +(1/x^3 ))=126 x^5 +(1/x^5 )+x+(1/x)=126 x^5 +(1/x^5 )+3=126 x^5 +(1/x^5 )=123

$${x}+\frac{\mathrm{1}}{{x}}=\mathrm{3}\:,\:{x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }=? \\ $$$$\blacktriangleright\left({x}+\frac{\mathrm{1}}{{x}}=\mathrm{3}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{7} \\ $$$$\blacktriangleright\left({x}+\frac{\mathrm{1}}{{x}}=\mathrm{3}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }+\mathrm{3}\left({x}+\frac{\mathrm{1}}{{x}}\right)=\mathrm{27} \\ $$$$\:\:\:\:{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\mathrm{18} \\ $$$$\blacktriangleright\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\left({x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)=\mathrm{126} \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }+{x}+\frac{\mathrm{1}}{{x}}=\mathrm{126} \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }+\mathrm{3}=\mathrm{126} \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }=\mathrm{123} \\ $$

Answered by Rasheed.Sindhi last updated on 29/Mar/25

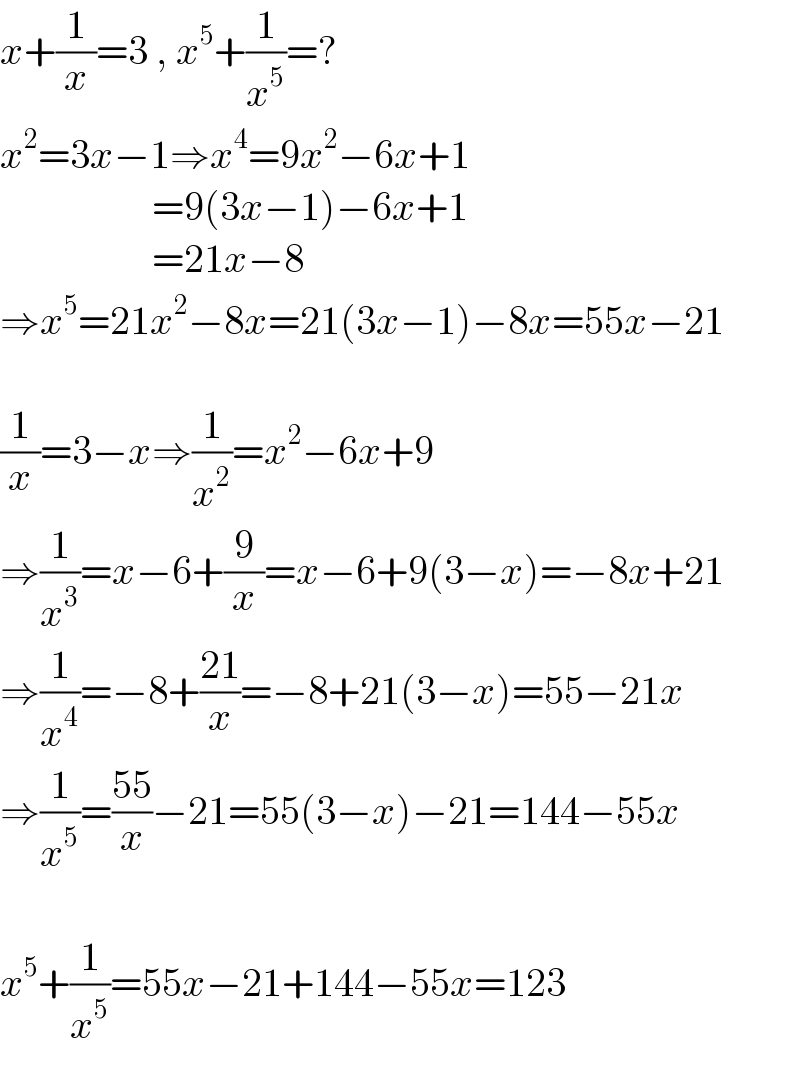
x+(1/x)=3 , x^5 +(1/x^5 )=? x^2 =3x−1⇒x^4 =9x^2 −6x+1 =9(3x−1)−6x+1 =21x−8 ⇒x^5 =21x^2 −8x=21(3x−1)−8x=55x−21 (1/x)=3−x⇒(1/x^2 )=x^2 −6x+9 ⇒(1/x^3 )=x−6+(9/x)=x−6+9(3−x)=−8x+21 ⇒(1/x^4 )=−8+((21)/x)=−8+21(3−x)=55−21x ⇒(1/x^5 )=((55)/x)−21=55(3−x)−21=144−55x x^5 +(1/x^5 )=55x−21+144−55x=123

$${x}+\frac{\mathrm{1}}{{x}}=\mathrm{3}\:,\:{x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }=? \\ $$$${x}^{\mathrm{2}} =\mathrm{3}{x}−\mathrm{1}\Rightarrow{x}^{\mathrm{4}} =\mathrm{9}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{9}\left(\mathrm{3}{x}−\mathrm{1}\right)−\mathrm{6}{x}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{21}{x}−\mathrm{8} \\ $$$$\Rightarrow{x}^{\mathrm{5}} =\mathrm{21}{x}^{\mathrm{2}} −\mathrm{8}{x}=\mathrm{21}\left(\mathrm{3}{x}−\mathrm{1}\right)−\mathrm{8}{x}=\mathrm{55}{x}−\mathrm{21} \\ $$$$\: \\ $$$$\frac{\mathrm{1}}{{x}}=\mathrm{3}−{x}\Rightarrow\frac{\mathrm{1}}{{x}^{\mathrm{2}} }={x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{9} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{x}^{\mathrm{3}} }={x}−\mathrm{6}+\frac{\mathrm{9}}{{x}}={x}−\mathrm{6}+\mathrm{9}\left(\mathrm{3}−{x}\right)=−\mathrm{8}{x}+\mathrm{21} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{x}^{\mathrm{4}} }=−\mathrm{8}+\frac{\mathrm{21}}{{x}}=−\mathrm{8}+\mathrm{21}\left(\mathrm{3}−{x}\right)=\mathrm{55}−\mathrm{21}{x} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{x}^{\mathrm{5}} }=\frac{\mathrm{55}}{{x}}−\mathrm{21}=\mathrm{55}\left(\mathrm{3}−{x}\right)−\mathrm{21}=\mathrm{144}−\mathrm{55}{x} \\ $$$$\: \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }=\mathrm{55}{x}−\mathrm{21}+\mathrm{144}−\mathrm{55}{x}=\mathrm{123} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com