
Question Number 85557 by naka3546 last updated on 23/Mar/20
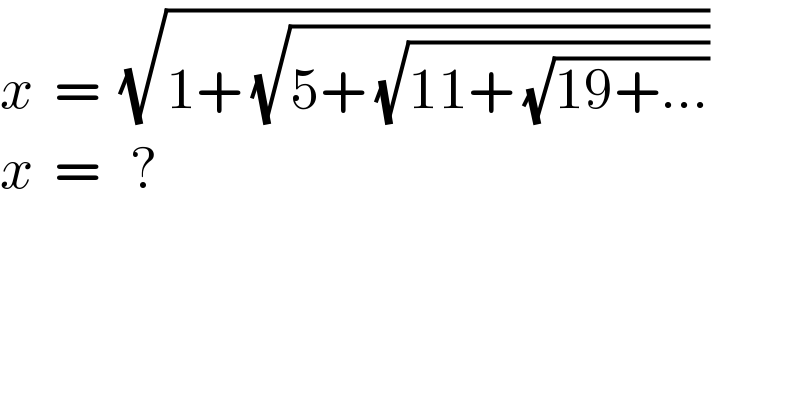
$${x}\:\:=\:\:\sqrt{\mathrm{1}+\:\sqrt{\mathrm{5}+\:\sqrt{\mathrm{11}+\:\sqrt{\mathrm{19}+...}}}} \\ $$$${x}\:\:=\:\:\:? \\ $$
Commented by MJS last updated on 23/Mar/20

$$\mathrm{2}? \\ $$
Commented by naka3546 last updated on 23/Mar/20

$${show}\:\:{your}\:\:{workings}\:,\:{please}\:. \\ $$
Commented by mr W last updated on 23/Mar/20
![n=(√n^2 )=(√([n^2 −(n+1)]+(n+1))) =(√([n^2 −(n+1)]+(√([(n+1)^2 −(n+2)]+(n+2))))) =(√([n^2 −(n+1)]+(√([(n+1)^2 −(n+2)]+(√([(n+2)^2 −(n+3)]+(n+3))))))) =(√([n^2 −(n+1)]+(√([(n+1)^2 −(n+2)]+(√([(n+2)^2 −(n+3)]+(√([(n+3)^2 −(n+4)]+(√(...)))))))))) ⇒n=(√([n^2 −(n+1)]+(√([(n+1)^2 −(n+2)]+(√([(n+2)^2 −(n+3)]+(√([(n+3)^2 −(n+4)]+(√(...)))))))))) let n=2: 2=(√(1+(√(5+(√(11+(√(19+(√(...))))))))))](Q85660.png)
$${n}=\sqrt{{n}^{\mathrm{2}} }=\sqrt{\left[{n}^{\mathrm{2}} −\left({n}+\mathrm{1}\right)\right]+\left({n}+\mathrm{1}\right)} \\ $$$$=\sqrt{\left[{n}^{\mathrm{2}} −\left({n}+\mathrm{1}\right)\right]+\sqrt{\left[\left({n}+\mathrm{1}\right)^{\mathrm{2}} −\left({n}+\mathrm{2}\right)\right]+\left({n}+\mathrm{2}\right)}} \\ $$$$=\sqrt{\left[{n}^{\mathrm{2}} −\left({n}+\mathrm{1}\right)\right]+\sqrt{\left[\left({n}+\mathrm{1}\right)^{\mathrm{2}} −\left({n}+\mathrm{2}\right)\right]+\sqrt{\left[\left({n}+\mathrm{2}\right)^{\mathrm{2}} −\left({n}+\mathrm{3}\right)\right]+\left({n}+\mathrm{3}\right)}}} \\ $$$$=\sqrt{\left[{n}^{\mathrm{2}} −\left({n}+\mathrm{1}\right)\right]+\sqrt{\left[\left({n}+\mathrm{1}\right)^{\mathrm{2}} −\left({n}+\mathrm{2}\right)\right]+\sqrt{\left[\left({n}+\mathrm{2}\right)^{\mathrm{2}} −\left({n}+\mathrm{3}\right)\right]+\sqrt{\left[\left({n}+\mathrm{3}\right)^{\mathrm{2}} −\left({n}+\mathrm{4}\right)\right]+\sqrt{...}}}}} \\ $$$$ \\ $$$$\Rightarrow{n}=\sqrt{\left[{n}^{\mathrm{2}} −\left({n}+\mathrm{1}\right)\right]+\sqrt{\left[\left({n}+\mathrm{1}\right)^{\mathrm{2}} −\left({n}+\mathrm{2}\right)\right]+\sqrt{\left[\left({n}+\mathrm{2}\right)^{\mathrm{2}} −\left({n}+\mathrm{3}\right)\right]+\sqrt{\left[\left({n}+\mathrm{3}\right)^{\mathrm{2}} −\left({n}+\mathrm{4}\right)\right]+\sqrt{...}}}}} \\ $$$${let}\:{n}=\mathrm{2}: \\ $$$$\mathrm{2}=\sqrt{\mathrm{1}+\sqrt{\mathrm{5}+\sqrt{\mathrm{11}+\sqrt{\mathrm{19}+\sqrt{...}}}}} \\ $$
