Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 101747 by Dwaipayan Shikari last updated on 04/Jul/20

∫(x^((−1)/2) /(1+x^(1/3) ))dx

$$\int\frac{{x}^{\frac{−\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}+{x}^{\frac{\mathrm{1}}{\mathrm{3}}} }{dx} \\ $$

Answered by bemath last updated on 04/Jul/20

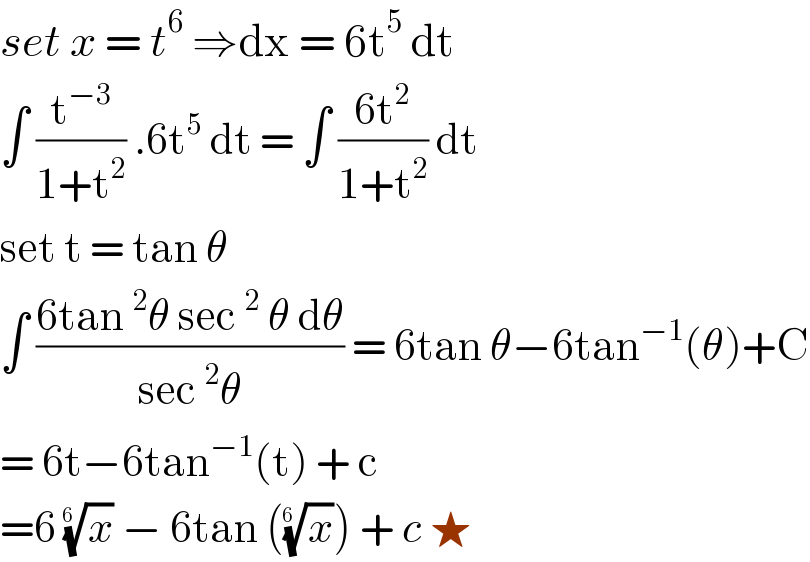
set x = t^6 ⇒dx = 6t^5 dt ∫ (t^(−3) /(1+t^2 )) .6t^5 dt = ∫ ((6t^2 )/(1+t^2 )) dt set t = tan θ ∫ ((6tan^2 θ sec^2 θ dθ)/(sec^2 θ)) = 6tan θ−6tan^(−1) (θ)+C = 6t−6tan^(−1) (t) + c =6 (x)^(1/(6 )) − 6tan ((x)^(1/(6 )) ) + c ★

$${set}\:{x}\:=\:{t}^{\mathrm{6}} \:\Rightarrow\mathrm{dx}\:=\:\mathrm{6t}^{\mathrm{5}} \:\mathrm{dt}\: \\ $$$$\int\:\frac{\mathrm{t}^{−\mathrm{3}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:.\mathrm{6t}^{\mathrm{5}} \:\mathrm{dt}\:=\:\int\:\frac{\mathrm{6t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:\mathrm{dt} \\ $$$$\mathrm{set}\:\mathrm{t}\:=\:\mathrm{tan}\:\theta \\ $$$$\int\:\frac{\mathrm{6tan}\:^{\mathrm{2}} \theta\:\mathrm{sec}\:^{\mathrm{2}} \:\theta\:\mathrm{d}\theta}{\mathrm{sec}\:^{\mathrm{2}} \theta}\:=\:\mathrm{6tan}\:\theta−\mathrm{6tan}^{−\mathrm{1}} \left(\theta\right)+\mathrm{C} \\ $$$$=\:\mathrm{6t}−\mathrm{6tan}^{−\mathrm{1}} \left(\mathrm{t}\right)\:+\:\mathrm{c} \\ $$$$=\mathrm{6}\:\sqrt[{\mathrm{6}\:}]{{x}}\:−\:\mathrm{6tan}\:\left(\sqrt[{\mathrm{6}\:}]{{x}}\right)\:+\:{c}\:\bigstar \\ $$

Commented by Dwaipayan Shikari last updated on 04/Jul/20

Great!

$$\boldsymbol{{Great}}! \\ $$

Commented by bemath last updated on 04/Jul/20

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com