
Question Number 195419 by CrispyXYZ last updated on 02/Aug/23
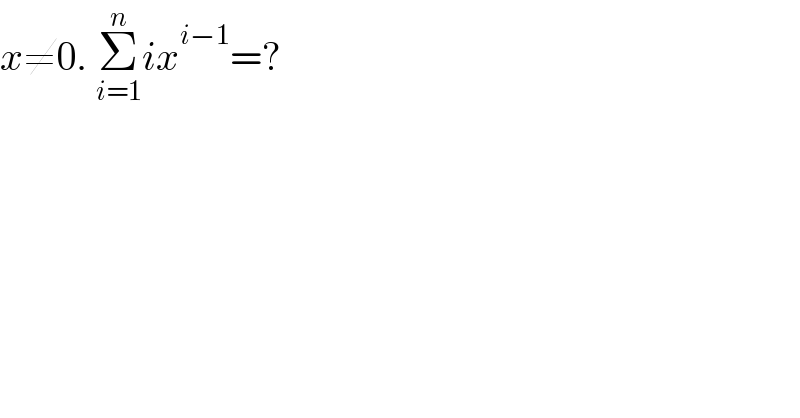
$${x}\neq\mathrm{0}.\:\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{ix}^{{i}−\mathrm{1}} =? \\ $$
Answered by MathedUp last updated on 02/Aug/23
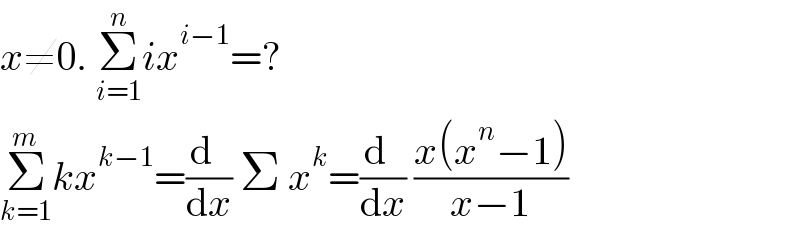
$${x}\neq\mathrm{0}.\:\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{ix}^{{i}−\mathrm{1}} =? \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}{kx}^{{k}−\mathrm{1}} =\frac{\mathrm{d}\:\:}{\mathrm{d}{x}}\:\Sigma\:{x}^{{k}} =\frac{\mathrm{d}\:\:}{\mathrm{d}{x}}\:\frac{{x}\left({x}^{{n}} −\mathrm{1}\right)}{{x}−\mathrm{1}} \\ $$
Commented by MathedUp last updated on 02/Aug/23
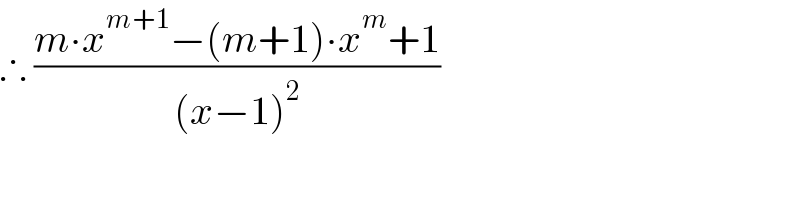
$$\therefore\:\frac{{m}\centerdot{x}^{{m}+\mathrm{1}} −\left({m}+\mathrm{1}\right)\centerdot{x}^{{m}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Commented by MathedUp last updated on 02/Aug/23
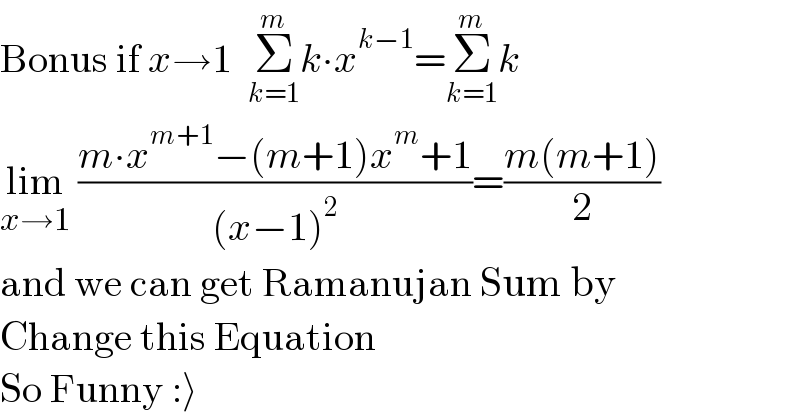
$$\mathrm{Bonus}\:\mathrm{if}\:{x}\rightarrow\mathrm{1}\:\:\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}{k}\centerdot{x}^{{k}−\mathrm{1}} =\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}{k} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{m}\centerdot{x}^{{m}+\mathrm{1}} −\left({m}+\mathrm{1}\right){x}^{{m}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }=\frac{{m}\left({m}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{we}\:\mathrm{can}\:\mathrm{get}\:\mathrm{Ramanujan}\:\mathrm{Sum}\:\mathrm{by} \\ $$$$\mathrm{Change}\:\mathrm{this}\:\mathrm{Equation} \\ $$$$\mathrm{So}\:\mathrm{Funny}\::\rangle \\ $$
