
Question Number 48956 by ggny last updated on 30/Nov/18
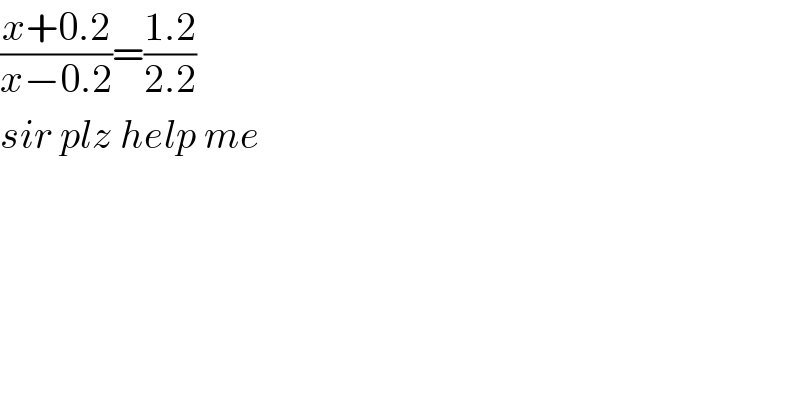
$$\frac{{x}+\mathrm{0}.\mathrm{2}}{{x}−\mathrm{0}.\mathrm{2}}=\frac{\mathrm{1}.\mathrm{2}}{\mathrm{2}.\mathrm{2}} \\ $$$${sir}\:{plz}\:{help}\:{me} \\ $$
Answered by kaivan.ahmadi last updated on 30/Nov/18
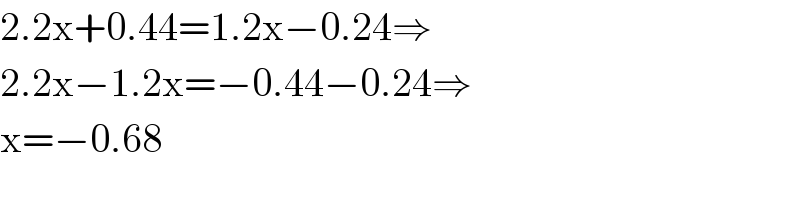
$$\mathrm{2}.\mathrm{2x}+\mathrm{0}.\mathrm{44}=\mathrm{1}.\mathrm{2x}−\mathrm{0}.\mathrm{24}\Rightarrow \\ $$$$\mathrm{2}.\mathrm{2x}−\mathrm{1}.\mathrm{2x}=−\mathrm{0}.\mathrm{44}−\mathrm{0}.\mathrm{24}\Rightarrow \\ $$$$\mathrm{x}=−\mathrm{0}.\mathrm{68} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 30/Nov/18

$$\mathrm{2}.\mathrm{2}{x}+\mathrm{0}.\mathrm{44}=\mathrm{1}.\mathrm{2}{x}−\mathrm{0}.\mathrm{24} \\ $$$$\mathrm{2}.\mathrm{2}{x}−\mathrm{1}.\mathrm{2}{x}=−\mathrm{0}.\mathrm{24}−\mathrm{0}.\mathrm{44} \\ $$$${x}=−\mathrm{0}.\mathrm{68} \\ $$
Answered by $@ty@m last updated on 01/Dec/18

$${It}'{s}\:{a}\:{good}\:{example}\:{to}\:{apply} \\ $$$${componendo}\:{and}\:{dividendo} \\ $$$$\frac{\left({x}+\mathrm{0}.\mathrm{2}\right)+\left({x}−\mathrm{0}.\mathrm{2}\right)}{\left({x}+\mathrm{0}.\mathrm{2}\right)−\left({x}−\mathrm{0}.\mathrm{2}\right)}=\frac{\mathrm{1}.\mathrm{2}+\mathrm{2}.\mathrm{2}}{\mathrm{1}.\mathrm{2}−\mathrm{2}.\mathrm{2}} \\ $$$$\frac{\mathrm{2}{x}}{\mathrm{0}.\mathrm{4}}=\frac{\mathrm{3}.\mathrm{4}}{−\mathrm{1}} \\ $$$${x}=−\mathrm{3}.\mathrm{4}×\mathrm{0}.\mathrm{2}=−\mathrm{0}.\mathrm{68} \\ $$
