
Question Number 66183 by 0ister D1Id0 last updated on 10/Aug/19
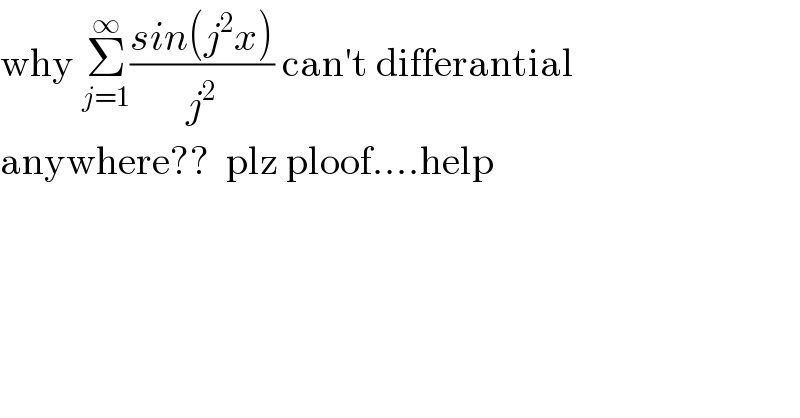
$$\mathrm{why}\:\underset{{j}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sin}\left({j}^{\mathrm{2}} {x}\right)}{{j}^{\mathrm{2}} }\:\mathrm{can}'\mathrm{t}\:\mathrm{differantial} \\ $$$$\mathrm{anywhere}??\:\:\mathrm{plz}\:\mathrm{ploof}....\mathrm{help} \\ $$
Commented by mathmax by abdo last updated on 10/Aug/19
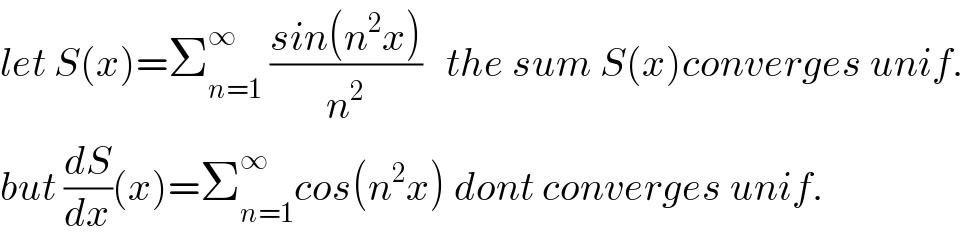
$${let}\:{S}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left({n}^{\mathrm{2}} {x}\right)}{{n}^{\mathrm{2}} }\:\:\:{the}\:{sum}\:{S}\left({x}\right){converges}\:{unif}. \\ $$$${but}\:\frac{{dS}}{{dx}}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} {cos}\left({n}^{\mathrm{2}} {x}\right)\:{dont}\:{converges}\:{unif}. \\ $$
