Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 214342 by issac last updated on 06/Dec/24

why differantiable f → f is continious but f is continous ↛ differantiable ??

$$\mathrm{why} \\ $$$$\mathrm{differantiable}\:{f}\:\rightarrow\:{f}\:\mathrm{is}\:\mathrm{continious}\: \\ $$$$\mathrm{but}\:{f}\:\mathrm{is}\:\mathrm{continous}\:\nrightarrow\:\mathrm{differantiable}\:?? \\ $$

Commented by mr W last updated on 06/Dec/24

a smooth line is always continous, but a continous line is not always smooth.

$${a}\:{smooth}\:{line}\:{is}\:{always}\:{continous}, \\ $$$${but}\:{a}\:{continous}\:{line}\:{is}\:{not}\:{always} \\ $$$${smooth}. \\ $$

Commented by mr W last updated on 06/Dec/24

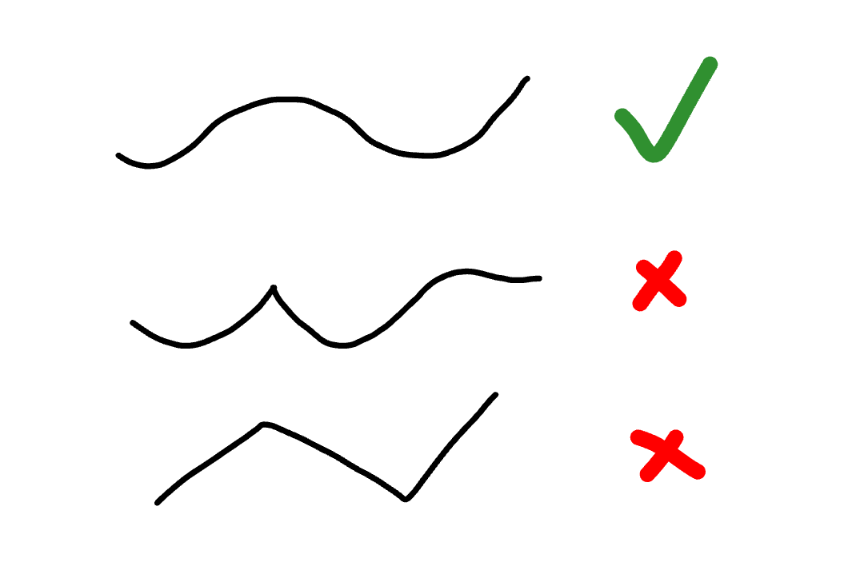
Commented by mr W last updated on 06/Dec/24

all are continious, but not all are smooth (differentiable).

$${all}\:{are}\:{continious},\:{but}\:{not}\:{all}\:{are} \\ $$$${smooth}\:\left({differentiable}\right). \\ $$

Answered by Frix last updated on 06/Dec/24

Just think of an example: f(x)=∣x∣ is continuous but not differentiable at x=0 g(x)=((x^2 −1))^(1/3) is continuous but not differentiable at x=±1

$$\mathrm{Just}\:\mathrm{think}\:\mathrm{of}\:\mathrm{an}\:\mathrm{example}: \\ $$$${f}\left({x}\right)=\mid{x}\mid\:\mathrm{is}\:\mathrm{continuous}\:\mathrm{but}\:\mathrm{not}\:\mathrm{differentiable} \\ $$$$\mathrm{at}\:{x}=\mathrm{0} \\ $$$${g}\left({x}\right)=\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} −\mathrm{1}}\:\mathrm{is}\:\mathrm{continuous}\:\mathrm{but}\:\mathrm{not}\:\mathrm{differentiable} \\ $$$$\mathrm{at}\:{x}=\pm\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com