Question and Answers Forum

All Questions      Topic List

Mechanics Questions

Previous in All Question      Next in All Question      

Previous in Mechanics      Next in Mechanics      

Question Number 174758 by Kallu last updated on 10/Aug/22

where am i wrong ?

$${where}\:{am}\:{i}\:{wrong}\:?\: \\ $$$$ \\ $$

Commented by Kallu last updated on 10/Aug/22

where am i wrong ? Correct answer is 5/4

$$ \\ $$$${where}\:{am}\:{i}\:{wrong}\:?\: \\ $$$${Correct}\:{answer}\:{is}\:\mathrm{5}/\mathrm{4} \\ $$

Commented by Kallu last updated on 10/Aug/22

Commented by Kallu last updated on 10/Aug/22

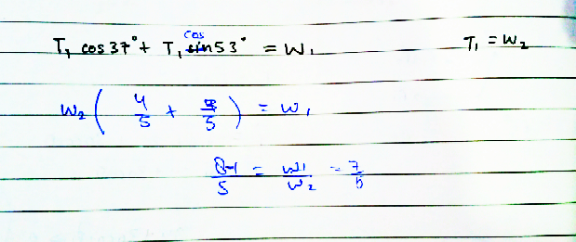
Answered by Ar Brandon last updated on 10/Aug/22

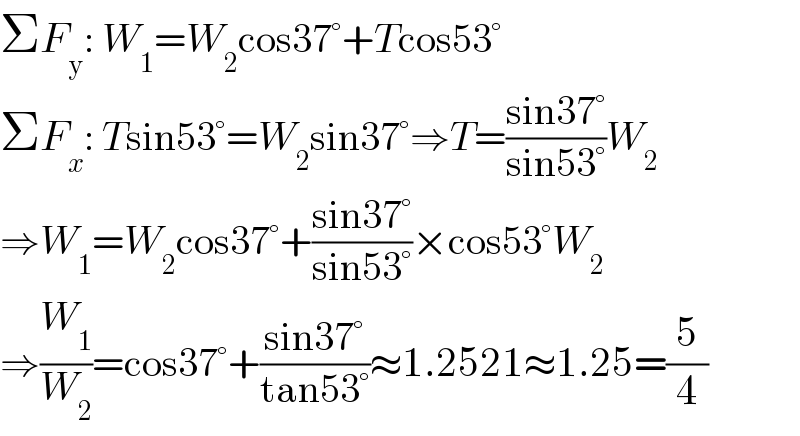
ΣF_y : W_1 =W_2 cos37°+Tcos53° ΣF_x : Tsin53°=W_2 sin37°⇒T=((sin37°)/(sin53°))W_2 ⇒W_1 =W_2 cos37°+((sin37°)/(sin53°))×cos53°W_2 ⇒(W_1 /W_2 )=cos37°+((sin37°)/(tan53°))≈1.2521≈1.25=(5/4)

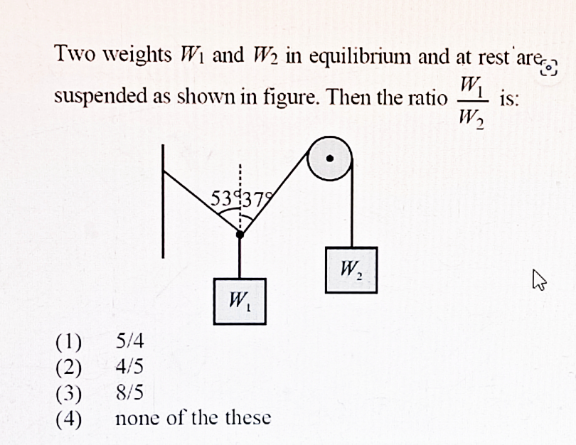
$$\Sigma{F}_{\mathrm{y}} :\:{W}_{\mathrm{1}} ={W}_{\mathrm{2}} \mathrm{cos37}°+{T}\mathrm{cos53}° \\ $$$$\Sigma{F}_{{x}} :\:{T}\mathrm{sin53}°={W}_{\mathrm{2}} \mathrm{sin37}°\Rightarrow{T}=\frac{\mathrm{sin37}°}{\mathrm{sin53}°}{W}_{\mathrm{2}} \\ $$$$\Rightarrow{W}_{\mathrm{1}} ={W}_{\mathrm{2}} \mathrm{cos37}°+\frac{\mathrm{sin37}°}{\mathrm{sin53}°}×\mathrm{cos53}°{W}_{\mathrm{2}} \\ $$$$\Rightarrow\frac{{W}_{\mathrm{1}} }{{W}_{\mathrm{2}} }=\mathrm{cos37}°+\frac{\mathrm{sin37}°}{\mathrm{tan53}°}\approx\mathrm{1}.\mathrm{2521}\approx\mathrm{1}.\mathrm{25}=\frac{\mathrm{5}}{\mathrm{4}} \\ $$

Commented by Kallu last updated on 11/Aug/22

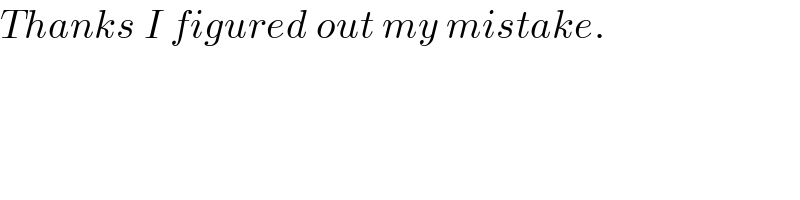
Thanks I figured out my mistake.

$${Thanks}\:{I}\:{figured}\:{out}\:{my}\:{mistake}. \\ $$$$ \\ $$

Commented by Tawa11 last updated on 12/Aug/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com