Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 193423 by mustafazaheen last updated on 13/Jun/23

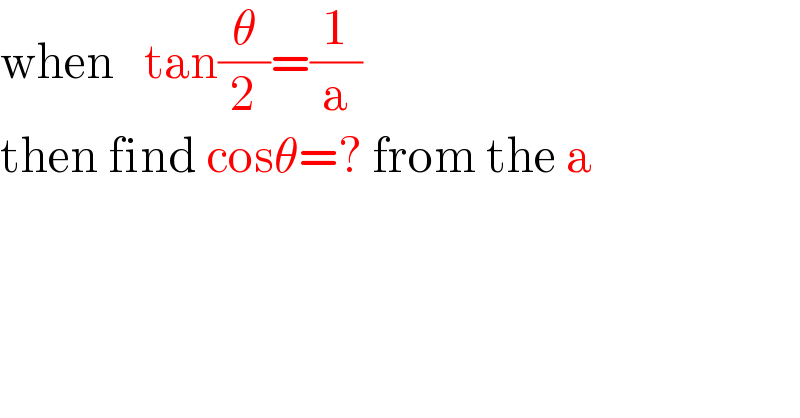
when tan(θ/2)=(1/a) then find cosθ=? from the a

$$\mathrm{when}\:\:\:\mathrm{tan}\frac{\theta}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{a}} \\ $$$$\mathrm{then}\:\mathrm{find}\:\mathrm{cos}\theta=?\:\mathrm{from}\:\mathrm{the}\:\mathrm{a} \\ $$

Answered by deleteduser1 last updated on 13/Jun/23

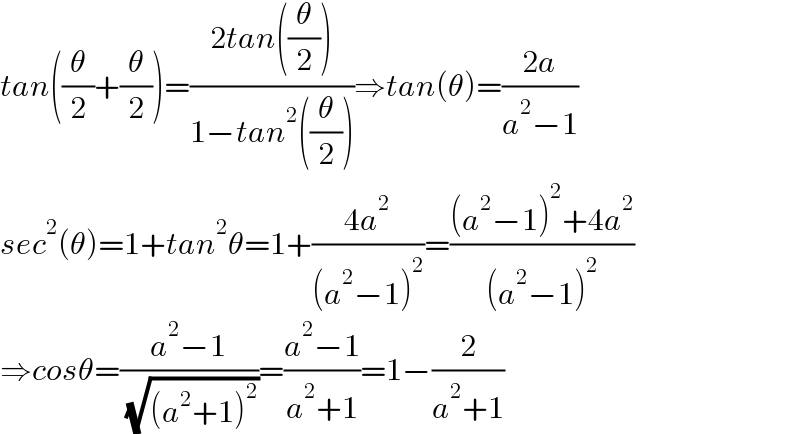
tan((θ/2)+(θ/2))=((2tan((θ/2)))/(1−tan^2 ((θ/2))))⇒tan(θ)=((2a)/(a^2 −1)) sec^2 (θ)=1+tan^2 θ=1+((4a^2 )/((a^2 −1)^2 ))=(((a^2 −1)^2 +4a^2 )/((a^2 −1)^2 )) ⇒cosθ=((a^2 −1)/( (√((a^2 +1)^2 ))))=((a^2 −1)/(a^2 +1))=1−(2/(a^2 +1))

$${tan}\left(\frac{\theta}{\mathrm{2}}+\frac{\theta}{\mathrm{2}}\right)=\frac{\mathrm{2}{tan}\left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{1}−{tan}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}\Rightarrow{tan}\left(\theta\right)=\frac{\mathrm{2}{a}}{{a}^{\mathrm{2}} −\mathrm{1}} \\ $$$${sec}^{\mathrm{2}} \left(\theta\right)=\mathrm{1}+{tan}^{\mathrm{2}} \theta=\mathrm{1}+\frac{\mathrm{4}{a}^{\mathrm{2}} }{\left({a}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }=\frac{\left({a}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} }{\left({a}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{cos}\theta=\frac{{a}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{\left({a}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }}=\frac{{a}^{\mathrm{2}} −\mathrm{1}}{{a}^{\mathrm{2}} +\mathrm{1}}=\mathrm{1}−\frac{\mathrm{2}}{{a}^{\mathrm{2}} +\mathrm{1}} \\ $$

Commented by mustafazaheen last updated on 13/Jun/23

T

$$\:\underbrace{{T}} \\ $$

Answered by Subhi last updated on 13/Jun/23

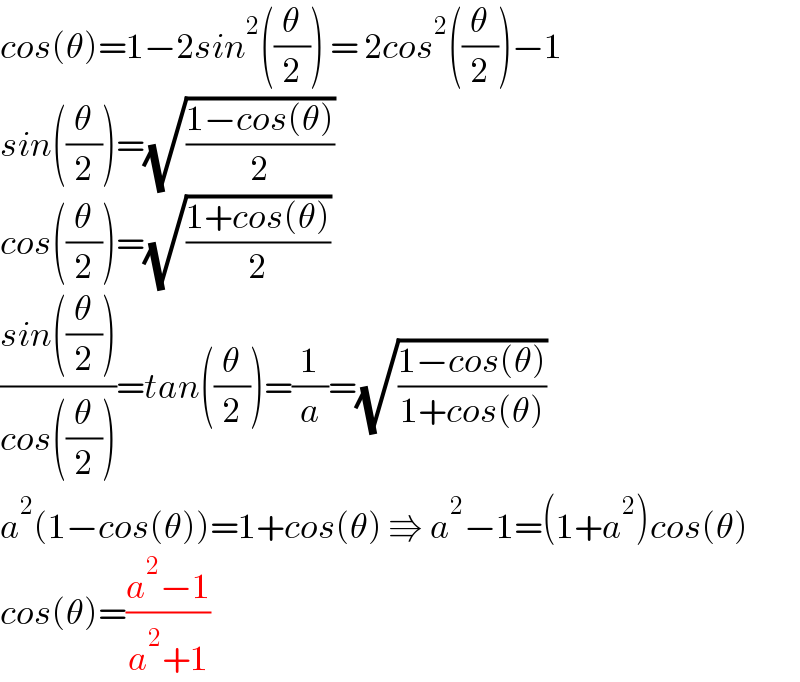
cos(θ)=1−2sin^2 ((θ/2)) = 2cos^2 ((θ/2))−1 sin((θ/2))=(√((1−cos(θ))/2)) cos((θ/2))=(√((1+cos(θ))/2)) ((sin((θ/2)))/(cos((θ/2))))=tan((θ/2))=(1/a)=(√((1−cos(θ))/(1+cos(θ)))) a^2 (1−cos(θ))=1+cos(θ) ⇛ a^2 −1=(1+a^2 )cos(θ) cos(θ)=((a^2 −1)/(a^2 +1))

$${cos}\left(\theta\right)=\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)\:=\:\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)−\mathrm{1} \\ $$$${sin}\left(\frac{\theta}{\mathrm{2}}\right)=\sqrt{\frac{\mathrm{1}−{cos}\left(\theta\right)}{\mathrm{2}}} \\ $$$${cos}\left(\frac{\theta}{\mathrm{2}}\right)=\sqrt{\frac{\mathrm{1}+{cos}\left(\theta\right)}{\mathrm{2}}} \\ $$$$\frac{{sin}\left(\frac{\theta}{\mathrm{2}}\right)}{{cos}\left(\frac{\theta}{\mathrm{2}}\right)}={tan}\left(\frac{\theta}{\mathrm{2}}\right)=\frac{\mathrm{1}}{{a}}=\sqrt{\frac{\mathrm{1}−{cos}\left(\theta\right)}{\mathrm{1}+{cos}\left(\theta\right)}} \\ $$$${a}^{\mathrm{2}} \left(\mathrm{1}−{cos}\left(\theta\right)\right)=\mathrm{1}+{cos}\left(\theta\right)\:\Rrightarrow\:{a}^{\mathrm{2}} −\mathrm{1}=\left(\mathrm{1}+{a}^{\mathrm{2}} \right){cos}\left(\theta\right) \\ $$$${cos}\left(\theta\right)=\frac{{a}^{\mathrm{2}} −\mathrm{1}}{{a}^{\mathrm{2}} +\mathrm{1}} \\ $$

Commented by mustafazaheen last updated on 13/Jun/23

⋛

$$\:\cancel{\lesseqgtr} \\ $$

Commented by York12 last updated on 16/Jun/23

⋛

$$\:\cancel{\lesseqgtr} \\ $$

Answered by BaliramKumar last updated on 13/Jun/23

cosθ = ((1−tan^2 ((θ/2)))/(1+tan^2 ((θ/2)))) = ((1−((1/a))^2 )/(1+((1/a))^2 )) = ((1−(1/a^2 ))/(1+(1/a^2 ))) cosθ = ((a^2 −1)/(a^2 +1)) pythagorean triplet⇒ 2a_(P) , (a^2 −1)_(B) , (a^2 +1)_(H) tanθ = ((2a)/(a^2 −1))

$$\mathrm{cos}\theta\:=\:\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}\:=\:\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{a}}\right)^{\mathrm{2}} }{\mathrm{1}+\left(\frac{\mathrm{1}}{\mathrm{a}}\right)^{\mathrm{2}} }\:=\:\:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }}\: \\ $$$$\mathrm{cos}\theta\:=\:\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}{\mathrm{a}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{pythagorean}\:\mathrm{triplet}\Rightarrow\:\underset{\mathrm{P}} {\underbrace{\mathrm{2a}}},\:\underset{\mathrm{B}} {\underbrace{\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)}},\:\underset{\mathrm{H}} {\underbrace{\left(\mathrm{a}^{\mathrm{2}} +\mathrm{1}\right)}} \\ $$$$\mathrm{tan}\theta\:=\:\frac{\mathrm{2a}}{\mathrm{a}^{\mathrm{2}} −\mathrm{1}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com