Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 94366 by i jagooll last updated on 18/May/20

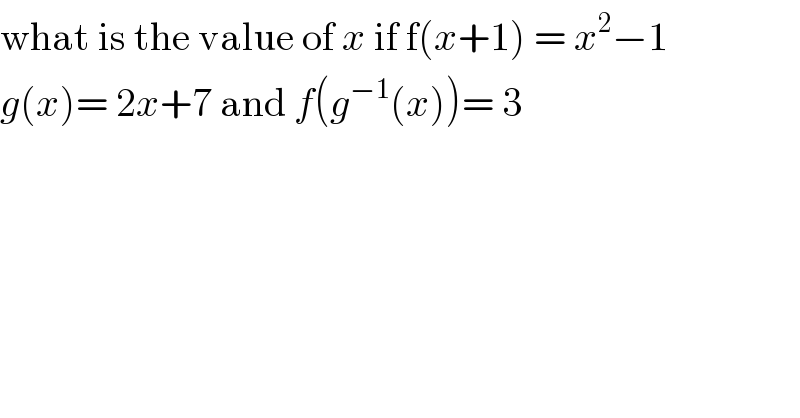
what is the value of x if f(x+1) = x^2 −1 g(x)= 2x+7 and f(g^(−1) (x))= 3

$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{x}\:\mathrm{if}\:\mathrm{f}\left({x}+\mathrm{1}\right)\:=\:{x}^{\mathrm{2}} −\mathrm{1} \\ $$$${g}\left({x}\right)=\:\mathrm{2}{x}+\mathrm{7}\:\mathrm{and}\:{f}\left({g}^{−\mathrm{1}} \left({x}\right)\right)=\:\mathrm{3}\: \\ $$

Commented by mr W last updated on 18/May/20

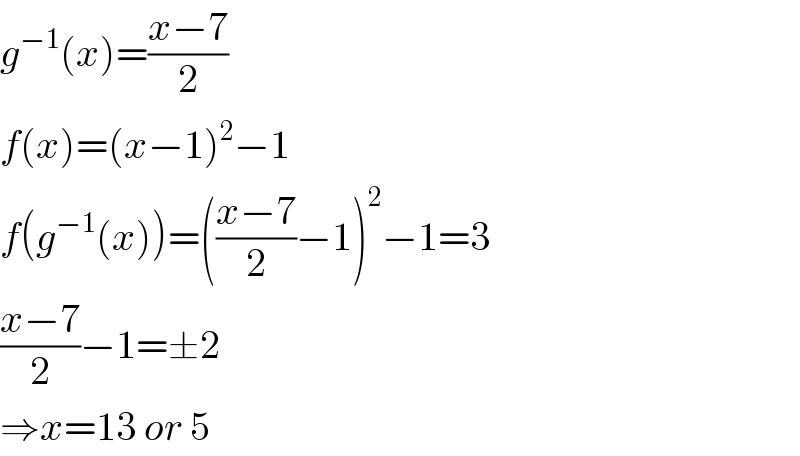
g^(−1) (x)=((x−7)/2) f(x)=(x−1)^2 −1 f(g^(−1) (x))=(((x−7)/2)−1)^2 −1=3 ((x−7)/2)−1=±2 ⇒x=13 or 5

$${g}^{−\mathrm{1}} \left({x}\right)=\frac{{x}−\mathrm{7}}{\mathrm{2}} \\ $$$${f}\left({x}\right)=\left({x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1} \\ $$$${f}\left({g}^{−\mathrm{1}} \left({x}\right)\right)=\left(\frac{{x}−\mathrm{7}}{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}=\mathrm{3} \\ $$$$\frac{{x}−\mathrm{7}}{\mathrm{2}}−\mathrm{1}=\pm\mathrm{2} \\ $$$$\Rightarrow{x}=\mathrm{13}\:{or}\:\mathrm{5} \\ $$

Commented by i jagooll last updated on 18/May/20

thank you both

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both} \\ $$

Commented by Abdulrahman last updated on 18/May/20

please solve this 3^x +x^3 =17 with steps

$$\mathrm{please} \\ $$$$\mathrm{solve} \\ $$$$\mathrm{this} \\ $$$$\mathrm{3}^{\mathrm{x}} +\mathrm{x}^{\mathrm{3}} =\mathrm{17} \\ $$$$\mathrm{with} \\ $$$$\mathrm{steps} \\ $$

Commented by mr W last updated on 18/May/20

1. we see (if you don′t see, then i can′t help you), that x=2 is a root, since 3^2 +2^3 =9+8=17. 2. both 3^x and x^3 are strictly increasing functions, so 3^x +x^3 is also strictly increasing. when a strictly increasing function has a zero, then this zero is the only one zero. that means x=2 is the only one root of eqn. x^2 +3^x =17.

$$\mathrm{1}.\:{we}\:{see}\:\left({if}\:{you}\:{don}'{t}\:{see},\:{then}\:{i}\:{can}'{t}\right. \\ $$$$\left.{help}\:{you}\right),\:{that}\:{x}=\mathrm{2}\:{is}\:{a}\:{root},\:{since} \\ $$$$\mathrm{3}^{\mathrm{2}} +\mathrm{2}^{\mathrm{3}} =\mathrm{9}+\mathrm{8}=\mathrm{17}. \\ $$$$\mathrm{2}.\:{both}\:\mathrm{3}^{{x}} \:{and}\:{x}^{\mathrm{3}} \:{are}\:{strictly}\:{increasing} \\ $$$${functions},\:{so}\:\mathrm{3}^{{x}} +{x}^{\mathrm{3}} \:{is}\:{also}\:{strictly} \\ $$$${increasing}.\:{when}\:{a}\:{strictly}\:{increasing} \\ $$$${function}\:{has}\:{a}\:{zero},\:{then}\:{this}\:{zero} \\ $$$${is}\:{the}\:{only}\:{one}\:{zero}.\:{that}\:{means} \\ $$$${x}=\mathrm{2}\:{is}\:{the}\:{only}\:{one}\:{root}\:{of}\:{eqn}. \\ $$$${x}^{\mathrm{2}} +\mathrm{3}^{{x}} =\mathrm{17}. \\ $$

Commented by Abdulrahman last updated on 18/May/20

bundle of thanks

$$\mathrm{bundle}\:\mathrm{of}\:\mathrm{thanks} \\ $$

Commented by Abdulrahman last updated on 18/May/20

∫(((x−2)^3 )/(2−x^2 ))dx=?

$$\int\frac{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{3}} }{\mathrm{2}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=? \\ $$

Commented by abdomathmax last updated on 18/May/20

I =∫ (((x−2)^3 )/(2−x^2 ))dx ⇒I =∫ ((x^3 −3x^2 ×2 +3x×2^2 −2^3 )/(2−x^2 ))dx =∫ ((x^3 −6x^2 +12x+8)/(2−x^2 )) dx =−∫((x^3 −6x^2 +12x+8)/(x^2 −2))dx =−∫ ((x(x^2 −2)−6x^2 +14x +8)/(x^2 −2))dx =−∫ xdx +∫ ((6x^2 −14x+8)/(x^2 −2))dx =−(x^2 /2) +∫ ((6(x^2 −2)−14x +20)/(x^2 −2))dx =−(x^2 /2) +6x −2∫ ((7x −10)/(x^2 −2))dx F(x)=((7x−10)/(x^2 −2)) =((7x−10)/((x−(√2))(x+(√2)))) =(a/(x−(√2))) +(b/(x+(√2))) a =((7(√2)−10)/(2(√2))) and b =((−7(√2)−10)/(−2(√2))) =((7(√2)+10)/(2(√2))) ∫((7x−10)/(x^2 −2))dx =((7(√2)−10)/(2(√2)))ln∣x−(√2)∣+((7(√2)+10)/(2(√2)))ln∣x+(√2)∣ +c I =−(x^2 /2) +6x−(7(√2)−10)ln∣x−(√2)∣−(7(√2)+10)ln∣x+(√2)∣ +C

$$\mathrm{I}\:=\int\:\:\frac{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{3}} }{\mathrm{2}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\mathrm{I}\:=\int\:\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{3x}^{\mathrm{2}} ×\mathrm{2}\:+\mathrm{3x}×\mathrm{2}^{\mathrm{2}} −\mathrm{2}^{\mathrm{3}} }{\mathrm{2}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\int\:\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{6x}^{\mathrm{2}} \:+\mathrm{12x}+\mathrm{8}}{\mathrm{2}−\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\:=−\int\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{6x}^{\mathrm{2}} \:+\mathrm{12x}+\mathrm{8}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}\mathrm{dx} \\ $$$$=−\int\:\:\frac{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2}\right)−\mathrm{6x}^{\mathrm{2}} \:+\mathrm{14x}\:+\mathrm{8}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}\mathrm{dx} \\ $$$$=−\int\:\mathrm{xdx}\:+\int\:\frac{\mathrm{6x}^{\mathrm{2}} −\mathrm{14x}+\mathrm{8}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:+\int\:\:\frac{\mathrm{6}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2}\right)−\mathrm{14x}\:+\mathrm{20}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:+\mathrm{6x}\:−\mathrm{2}\int\:\:\frac{\mathrm{7x}\:−\mathrm{10}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}\mathrm{dx} \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{7x}−\mathrm{10}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}\:=\frac{\mathrm{7x}−\mathrm{10}}{\left(\mathrm{x}−\sqrt{\mathrm{2}}\right)\left(\mathrm{x}+\sqrt{\mathrm{2}}\right)}\:=\frac{\mathrm{a}}{\mathrm{x}−\sqrt{\mathrm{2}}}\:+\frac{\mathrm{b}}{\mathrm{x}+\sqrt{\mathrm{2}}} \\ $$$$\mathrm{a}\:=\frac{\mathrm{7}\sqrt{\mathrm{2}}−\mathrm{10}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\mathrm{and}\:\mathrm{b}\:=\frac{−\mathrm{7}\sqrt{\mathrm{2}}−\mathrm{10}}{−\mathrm{2}\sqrt{\mathrm{2}}}\:=\frac{\mathrm{7}\sqrt{\mathrm{2}}+\mathrm{10}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\int\frac{\mathrm{7x}−\mathrm{10}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}\mathrm{dx}\:=\frac{\mathrm{7}\sqrt{\mathrm{2}}−\mathrm{10}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\mathrm{x}−\sqrt{\mathrm{2}}\mid+\frac{\mathrm{7}\sqrt{\mathrm{2}}+\mathrm{10}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\mathrm{x}+\sqrt{\mathrm{2}}\mid\:+\mathrm{c} \\ $$$$\mathrm{I}\:=−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:+\mathrm{6x}−\left(\mathrm{7}\sqrt{\mathrm{2}}−\mathrm{10}\right)\mathrm{ln}\mid\mathrm{x}−\sqrt{\mathrm{2}}\mid−\left(\mathrm{7}\sqrt{\mathrm{2}}+\mathrm{10}\right)\mathrm{ln}\mid\mathrm{x}+\sqrt{\mathrm{2}}\mid\:+\mathrm{C} \\ $$

Commented by mr W last updated on 18/May/20

abdulraman sir: please open a new thread if you want to ask a new question!

$${abdulraman}\:{sir}: \\ $$$${please}\:{open}\:{a}\:{new}\:{thread}\:{if}\:{you}\:{want} \\ $$$${to}\:{ask}\:{a}\:{new}\:{question}! \\ $$

Commented by Abdulrahman last updated on 18/May/20

ok thanks alot

$$\mathrm{ok}\:\mathrm{thanks}\:\mathrm{alot} \\ $$

Answered by john santu last updated on 18/May/20

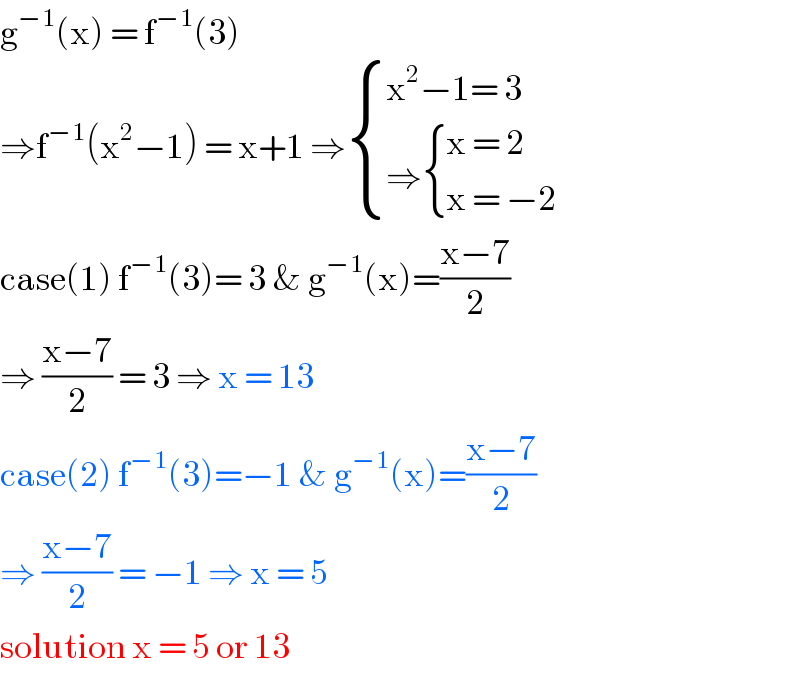
g^(−1) (x) = f^(−1) (3) ⇒f^(−1) (x^2 −1) = x+1 ⇒ { ((x^2 −1= 3)),((⇒ { ((x = 2)),((x = −2)) :})) :} case(1) f^(−1) (3)= 3 & g^(−1) (x)=((x−7)/2) ⇒ ((x−7)/2) = 3 ⇒ x = 13 case(2) f^(−1) (3)=−1 & g^(−1) (x)=((x−7)/2) ⇒ ((x−7)/2) = −1 ⇒ x = 5 solution x = 5 or 13

$$\mathrm{g}^{−\mathrm{1}} \left(\mathrm{x}\right)\:=\:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{3}\right)\: \\ $$$$\Rightarrow\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\:=\:\mathrm{x}+\mathrm{1}\:\Rightarrow\begin{cases}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}=\:\mathrm{3}}\\{\Rightarrow\begin{cases}{\mathrm{x}\:=\:\mathrm{2}}\\{\mathrm{x}\:=\:−\mathrm{2}}\end{cases}}\end{cases} \\ $$$$\mathrm{case}\left(\mathrm{1}\right)\:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{3}\right)=\:\mathrm{3}\:\&\:\mathrm{g}^{−\mathrm{1}} \left(\mathrm{x}\right)=\frac{\mathrm{x}−\mathrm{7}}{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{\mathrm{x}−\mathrm{7}}{\mathrm{2}}\:=\:\mathrm{3}\:\Rightarrow\:\mathrm{x}\:=\:\mathrm{13}\: \\ $$$$\mathrm{case}\left(\mathrm{2}\right)\:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{3}\right)=−\mathrm{1}\:\&\:\mathrm{g}^{−\mathrm{1}} \left(\mathrm{x}\right)=\frac{\mathrm{x}−\mathrm{7}}{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{\mathrm{x}−\mathrm{7}}{\mathrm{2}}\:=\:−\mathrm{1}\:\Rightarrow\:\mathrm{x}\:=\:\mathrm{5}\: \\ $$$$\mathrm{solution}\:\mathrm{x}\:=\:\mathrm{5}\:\mathrm{or}\:\mathrm{13}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com