
Question Number 214329 by malwan last updated on 05/Dec/24
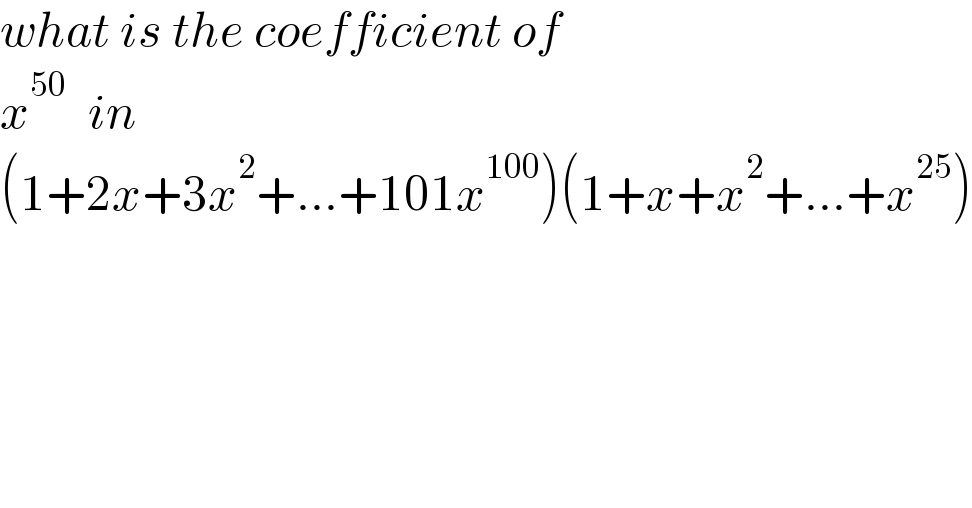
$${what}\:{is}\:{the}\:{coefficient}\:{of} \\ $$$${x}^{\mathrm{50}\:\:} \:{in} \\ $$$$\left(\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +...+\mathrm{101}{x}^{\mathrm{100}} \right)\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +...+{x}^{\mathrm{25}} \right) \\ $$
Answered by mr W last updated on 05/Dec/24

$$\mathrm{51}+\mathrm{50}+\mathrm{49}+...+\mathrm{26} \\ $$$$=\frac{\left(\mathrm{51}+\mathrm{26}\right)×\mathrm{26}}{\mathrm{2}}=\mathrm{1001}\:\checkmark \\ $$
Commented by malwan last updated on 06/Dec/24

Answered by A5T last updated on 05/Dec/24
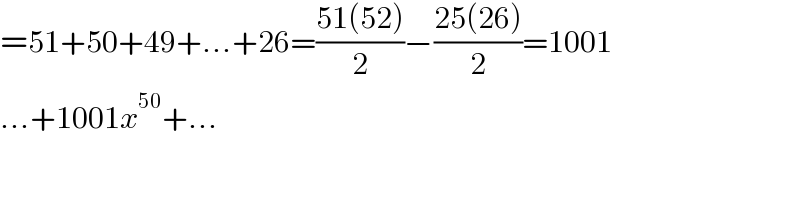
$$=\mathrm{51}+\mathrm{50}+\mathrm{49}+...+\mathrm{26}=\frac{\mathrm{51}\left(\mathrm{52}\right)}{\mathrm{2}}−\frac{\mathrm{25}\left(\mathrm{26}\right)}{\mathrm{2}}=\mathrm{1001} \\ $$$$...+\mathrm{1001}{x}^{\mathrm{50}} +... \\ $$
Commented by malwan last updated on 06/Dec/24

$${thank}\:{you}\:{sir} \\ $$
