
Question Number 76842 by jagoll last updated on 31/Dec/19
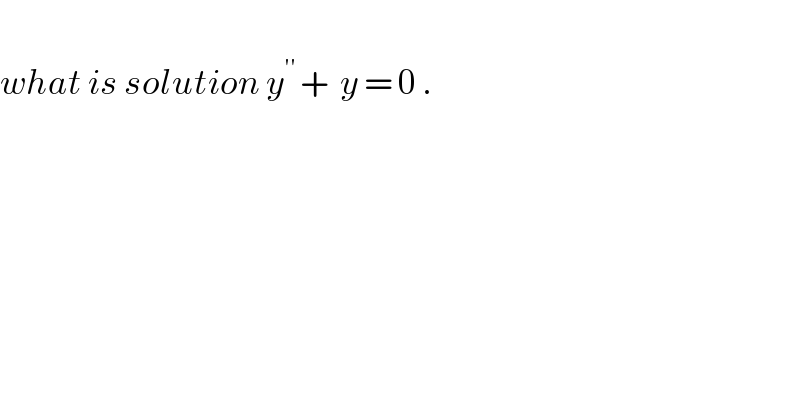
$$ \\ $$$${what}\:{is}\:{solution}\:{y}^{''\:} +\:\:{y}\:=\:\mathrm{0}\:. \\ $$
Commented by mathmax by abdo last updated on 31/Dec/19
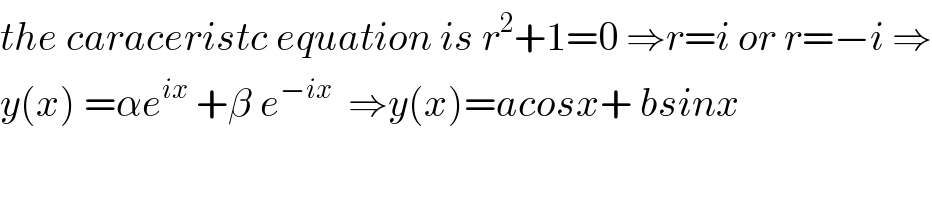
$${the}\:{caraceristc}\:{equation}\:{is}\:{r}^{\mathrm{2}} +\mathrm{1}=\mathrm{0}\:\Rightarrow{r}={i}\:{or}\:{r}=−{i}\:\Rightarrow \\ $$$${y}\left({x}\right)\:=\alpha{e}^{{ix}} \:+\beta\:{e}^{−{ix}} \:\:\Rightarrow{y}\left({x}\right)={acosx}+\:{bsinx} \\ $$
Answered by mr W last updated on 31/Dec/19
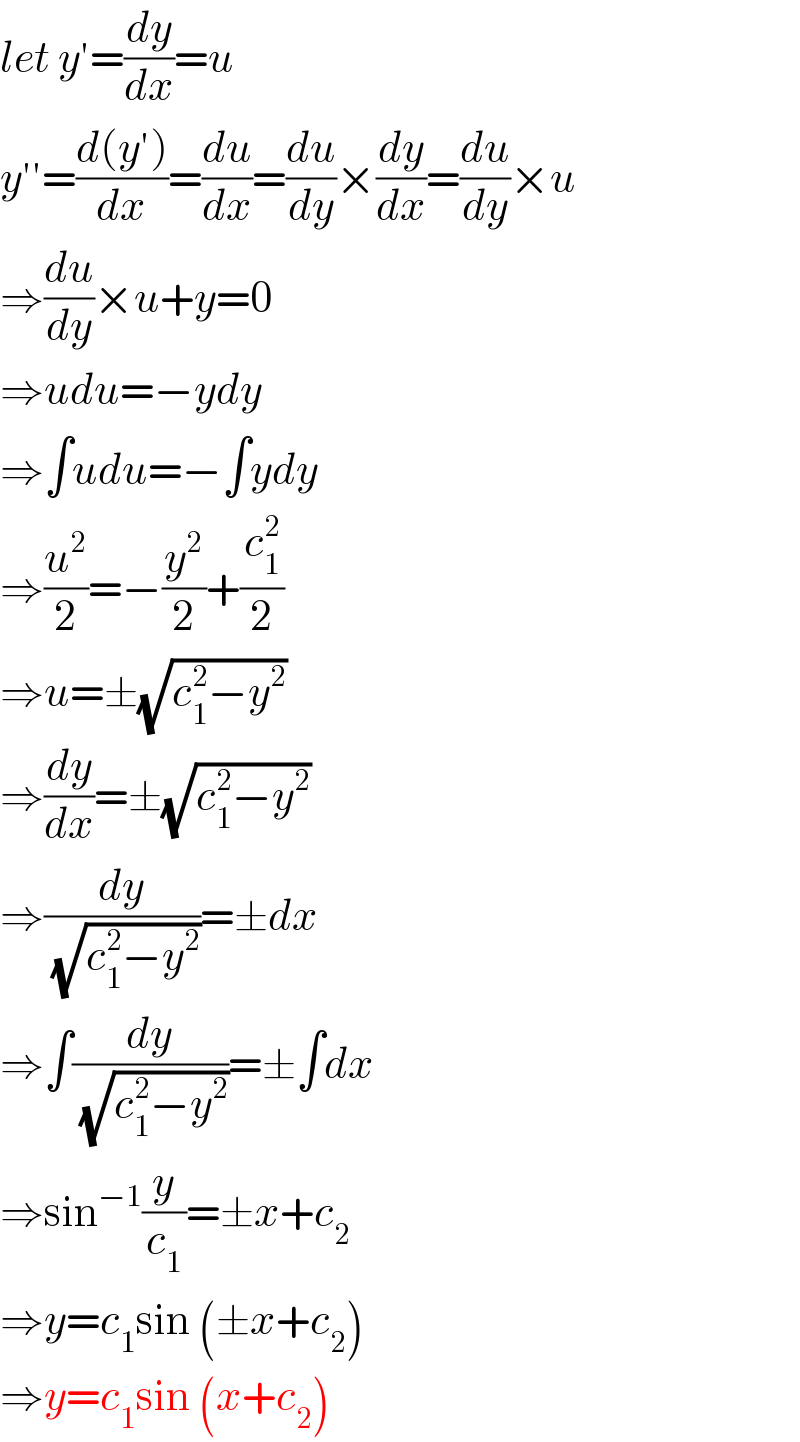
$${let}\:{y}'=\frac{{dy}}{{dx}}={u} \\ $$$${y}''=\frac{{d}\left({y}'\right)}{{dx}}=\frac{{du}}{{dx}}=\frac{{du}}{{dy}}×\frac{{dy}}{{dx}}=\frac{{du}}{{dy}}×{u} \\ $$$$\Rightarrow\frac{{du}}{{dy}}×{u}+{y}=\mathrm{0} \\ $$$$\Rightarrow{udu}=−{ydy} \\ $$$$\Rightarrow\int{udu}=−\int{ydy} \\ $$$$\Rightarrow\frac{{u}^{\mathrm{2}} }{\mathrm{2}}=−\frac{{y}^{\mathrm{2}} }{\mathrm{2}}+\frac{{c}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow{u}=\pm\sqrt{{c}_{\mathrm{1}} ^{\mathrm{2}} −{y}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=\pm\sqrt{{c}_{\mathrm{1}} ^{\mathrm{2}} −{y}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{dy}}{\sqrt{{c}_{\mathrm{1}} ^{\mathrm{2}} −{y}^{\mathrm{2}} }}=\pm{dx} \\ $$$$\Rightarrow\int\frac{{dy}}{\sqrt{{c}_{\mathrm{1}} ^{\mathrm{2}} −{y}^{\mathrm{2}} }}=\pm\int{dx} \\ $$$$\Rightarrow\mathrm{sin}^{−\mathrm{1}} \frac{{y}}{{c}_{\mathrm{1}} }=\pm{x}+{c}_{\mathrm{2}} \\ $$$$\Rightarrow{y}={c}_{\mathrm{1}} \mathrm{sin}\:\left(\pm{x}+{c}_{\mathrm{2}} \right) \\ $$$$\Rightarrow{y}={c}_{\mathrm{1}} \mathrm{sin}\:\left({x}+{c}_{\mathrm{2}} \right) \\ $$
Commented by jagoll last updated on 31/Dec/19

$${thanks}\:{you}\:{sir} \\ $$
Commented by jagoll last updated on 31/Dec/19
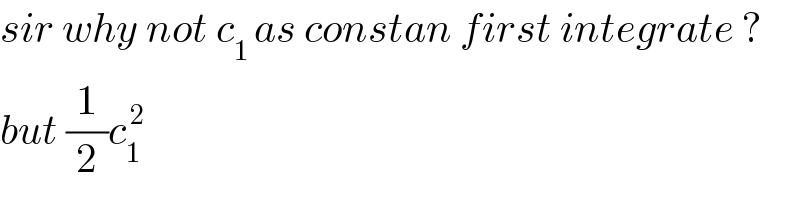
$${sir}\:{why}\:{not}\:{c}_{\mathrm{1}\:} {as}\:{constan}\:{first}\:{integrate}\:?\: \\ $$$${but}\:\frac{\mathrm{1}}{\mathrm{2}}{c}_{\mathrm{1}\:} ^{\:\mathrm{2}\:} \\ $$
Commented by mr W last updated on 31/Dec/19

$${it}\:{makes}\:{no}\:{real}\:{difference},\:{but} \\ $$$${looks}\:{better}\:{in}\:{later}\:{operations}. \\ $$
Commented by jagoll last updated on 31/Dec/19
$${oo}\:{ok}\:{sir}\:{thanks}\:{you} \\ $$
Answered by Rio Michael last updated on 18/Jan/20

$${i}\:{could}\:{also}\:{solve}\:{this}\:{by}\: \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} \:}\:+\:{y}\:=\:\mathrm{0} \\ $$$${the}\:{auxiliary}\:{equation}\:{is} \\ $$$${r}^{\mathrm{2}} \:+\:\mathrm{1}\:=\:\mathrm{0}\:\:\Rightarrow\:{r}=\:{i}\:{or}\:{r}\:=\:−{i} \\ $$$${or}\:\:{r}\:=\:\mathrm{0}\:+\:{i}\:{and}\:{r}\:=\:\mathrm{0}−{i}\: \\ $$$${the}\:{general}\:{solution} \\ $$$${is}\:{of}\:{the}\:{firm}\:\:{y}\:=\:{e}^{{px}} \left({Acosqx}\:+{B}\:{sinqx}\right) \\ $$$${where}\:{p}\:=\mathrm{0}\:{and}\:{q}=\mathrm{1} \\ $$$${y}\:=\:{Acos}\:{x}\:+\:{Bsinx} \\ $$
