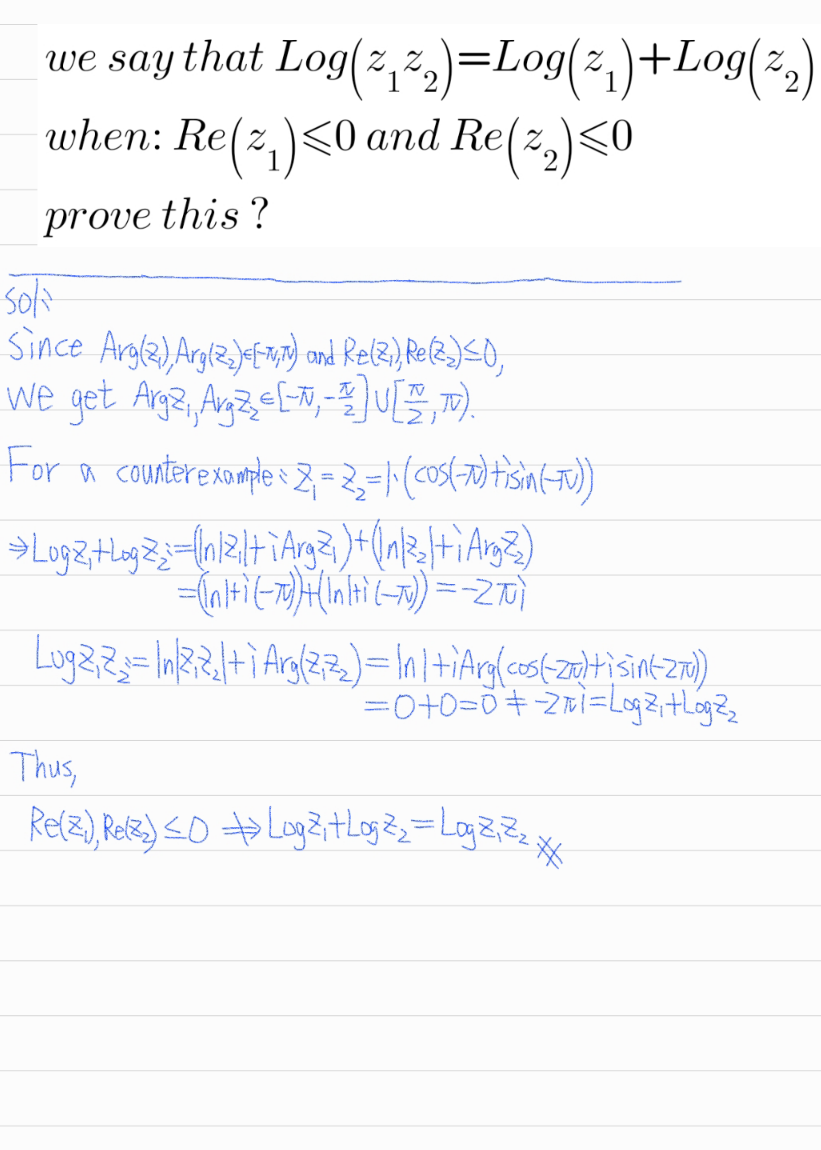Question Number 132032 by mohammad17 last updated on 10/Feb/21
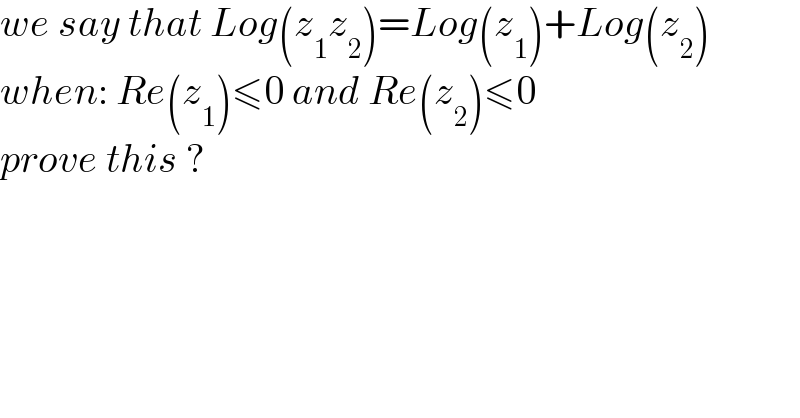
$${we}\:{say}\:{that}\:{Log}\left({z}_{\mathrm{1}} {z}_{\mathrm{2}} \right)={Log}\left({z}_{\mathrm{1}} \right)+{Log}\left({z}_{\mathrm{2}} \right) \\ $$$${when}:\:{Re}\left({z}_{\mathrm{1}} \right)\leqslant\mathrm{0}\:{and}\:{Re}\left({z}_{\mathrm{2}} \right)\leqslant\mathrm{0} \\ $$$${prove}\:{this}\:? \\ $$
Commented by mohammad17 last updated on 10/Feb/21
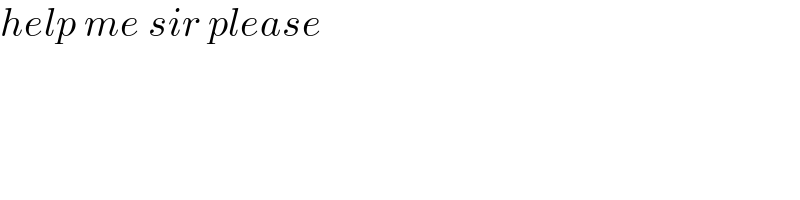
$${help}\:{me}\:{sir}\:{please} \\ $$
Commented by mohammad17 last updated on 10/Feb/21

$${sir} \\ $$$${log}\left({z}\right)\neq{Log}\left({z}\right) \\ $$
Commented by yjjyguuh6uhh last updated on 10/Feb/21

$${below} \\ $$
Commented by yjjyguuh6uhh last updated on 10/Feb/21