
Previous in Relation and Functions Next in Relation and Functions
Question Number 30483 by abdo imad last updated on 22/Feb/18
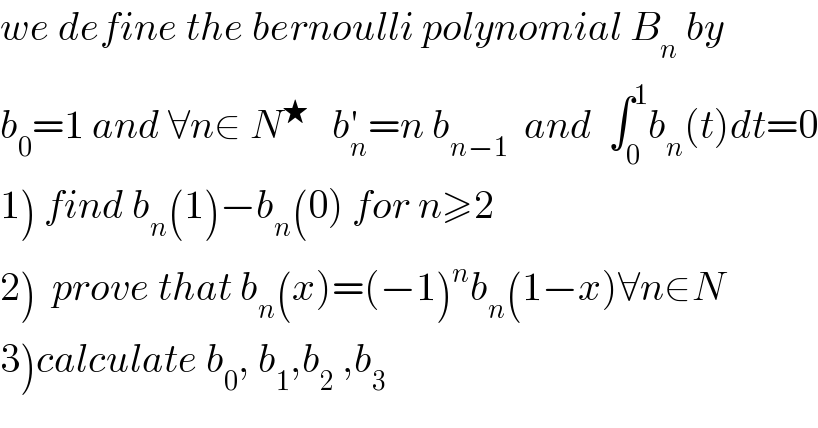
$${we}\:{define}\:{the}\:{bernoulli}\:{polynomial}\:{B}_{{n}} \:{by} \\ $$$${b}_{\mathrm{0}} =\mathrm{1}\:{and}\:\forall{n}\in\:{N}^{\bigstar} \:\:\:{b}_{{n}} ^{'} ={n}\:{b}_{{n}−\mathrm{1}} \:\:{and}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} {b}_{{n}} \left({t}\right){dt}=\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{b}_{{n}} \left(\mathrm{1}\right)−{b}_{{n}} \left(\mathrm{0}\right)\:{for}\:{n}\geqslant\mathrm{2} \\ $$$$\left.\mathrm{2}\right)\:\:{prove}\:{that}\:{b}_{{n}} \left({x}\right)=\left(−\mathrm{1}\right)^{{n}} {b}_{{n}} \left(\mathrm{1}−{x}\right)\forall{n}\in{N} \\ $$$$\left.\mathrm{3}\right){calculate}\:{b}_{\mathrm{0}} ,\:{b}_{\mathrm{1}} ,{b}_{\mathrm{2}} \:,{b}_{\mathrm{3}} \\ $$
