Question Number 210956 by mahdipoor last updated on 23/Aug/24
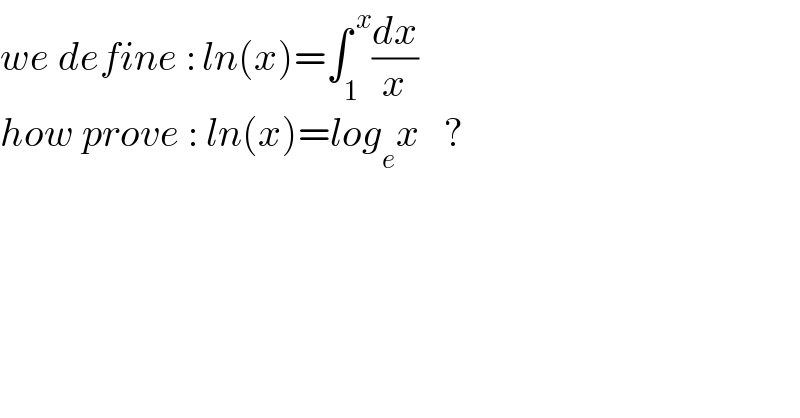
$${we}\:{define}\::\:{ln}\left({x}\right)=\int_{\mathrm{1}} ^{\:{x}} \frac{{dx}}{{x}} \\ $$$${how}\:{prove}\::\:{ln}\left({x}\right)={log}_{{e}} {x}\:\:\:? \\ $$
Commented by Ghisom last updated on 24/Aug/24
$$\mathrm{an}\:\mathrm{idea}: \\ $$$$\mathrm{the}\:\mathrm{area}\:\mathrm{between}\:{y}=\mathrm{0}\:\mathrm{and}\:{y}=\underset{\mathrm{1}} {\overset{{b}} {\int}}\:\frac{{dx}}{{x}}\:\mathrm{must} \\ $$$$\mathrm{be}\:\mathrm{1}\:\mathrm{for}\:\mathrm{the}\:\mathrm{base}\:{b}\:\mathrm{of}\:\mathrm{the}\:\mathrm{logarithm}. \\ $$$$\mathrm{use}\:\mathrm{any}\:\mathrm{approximation}\:\mathrm{formula}\:\mathrm{for}\:\mathrm{areas} \\ $$$$\mathrm{under}\:\mathrm{curves}. \\ $$$$ \\ $$$$\mathrm{also}\:\mathrm{possible}:\:\mathrm{adding}\:\mathrm{up}\:\mathrm{rectangles}\:\mathrm{until} \\ $$$$\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{their}\:\mathrm{areas}\:\mathrm{exceed}\:\mathrm{1}: \\ $$$$\mathrm{width}\:\frac{\mathrm{1}}{\mathrm{10}}\:\Rightarrow\:{b}\approx\mathrm{2}.\mathrm{6}... \\ $$$$\mathrm{width}\:\frac{\mathrm{1}}{\mathrm{100}}\:\Rightarrow\:{b}\approx\mathrm{2}.\mathrm{7}... \\ $$$$\mathrm{width}\:\frac{\mathrm{1}}{\mathrm{1000}}\:\Rightarrow\:{b}\approx\mathrm{2}.\mathrm{717}... \\ $$$$\mathrm{width}\:\frac{\mathrm{1}}{\mathrm{10000}}\:\Rightarrow\:{b}\approx\mathrm{2}.\mathrm{7182}... \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{intuitive}\:\mathrm{but}\:\mathrm{converges}\:\mathrm{slowly} \\ $$
Answered by mm1342 last updated on 24/Aug/24
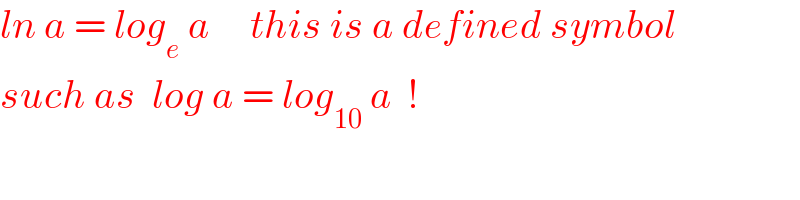
$${ln}\:{a}\:=\:{log}_{{e}} \:{a}\:\:\:\:\:{this}\:{is}\:{a}\:{defined}\:{symbol} \\ $$$${such}\:{as}\:\:{log}\:{a}\:=\:{log}_{\mathrm{10}} \:{a}\:\:! \\ $$
Commented by mahdipoor last updated on 24/Aug/24
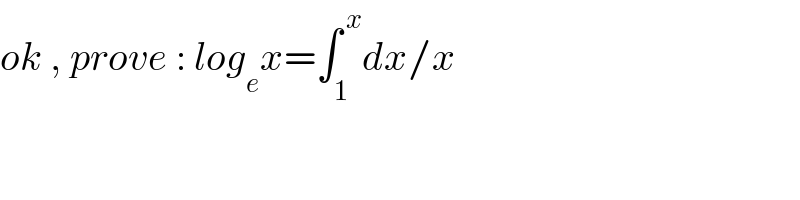
$${ok}\:,\:{prove}\::\:{log}_{{e}} {x}=\int_{\mathrm{1}} ^{\:{x}} {dx}/{x} \\ $$
Commented by mm1342 last updated on 24/Aug/24
$$\:\underline{\underbrace{\lesseqgtr}} \\ $$